Теорема 1. Для любых двух несмежных вершин и и x графа G наибольшее число реберно-непересекающихся u, x -цепей равно наименьшему числу ребер в (u, x)-разрезе.

Теорема 2. Чтобы граф G был n-связным, необходимо и достаточно, чтобы любые две несмежные вершины были соединены не менее чем n вершиннонепересекающимися простыми цепями.

Другими словами, в любом графе G любые две несмежные вершины соединены не менее чем (G) вершинно-непересекающимися простыми цепями. Доказательство подобных утверждений требует места, и мы оставляем их за пределами книги. В последующих разделах пособия приведены также некоторые другие результаты, в которых проявляется теорема Менгера.

2.5. Теорема Холла

Пусть G (X1, X2, V) – двудольный граф. Совершенное паросочетание из X1 в X2 существует тогда и только тогда, когда

A X1 ( A Г(A) ) .

Паросочетанием называется множество ребер, в котором никакие два ребра не смежны. Паросочетание называется максимальным, если никакое его надмножество не является независимым. Пусть G (X1, X2, V) – двудольный граф. Совершенным паросочетанием из X1 в X2 называется паросочетание, покрывающее вершины X1.

Доказательство.

[ ] Пусть существует совершенное паросочетание из X1 в X2. Тогда в Г(А) входит A вершин из X2, парных к вершинам из множества А. Таким образом,

A Г(A) .

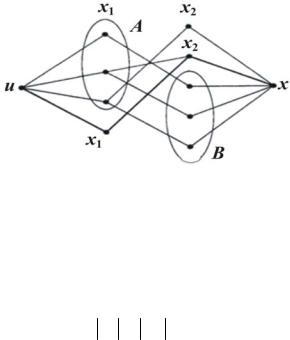
[ ] Добавим в G две новые вершины u и x, так, что вершина и смежна со всеми вершинами из X1, а вершина x – со всеми вершинами из X2. Совершенное паросочетание из X1 в X2 существует тогда и только тогда, когда существует |X1| вершинно-непересекающихся простых u, x -цепей (рис. 20). Ясно, что P(u, x) X1 (так как X1 разделяет вершины u и x).

Рис. 20. К доказательству теоремы Холла

По теореме Менгера

max |P(u, x)| = min |S(u, x)| = |S|,

где S – наименьшее множество, разделяющее вершины и и x. Имеем |S| < |X1|. Покажем, что S X1 .

Пусть S A B, A X1, B X 2 .

Тогда Г(X1 \ А) В. Действительно, если бы Г(X1 \ А) В, то существовал бы «обходной» путь u, x1 , x2 , x (см. рис. 20) и S не было бы разделяющим

множеством для и и x. Имеем |X1 \ А| |Г(X1 \ А)| |В|. Следовательно,

|S| = |А| + |В| |А| + |X1 \ А| = |X1|.

2.6. Связность в орграфах

Сильная, односторонняя и слабая связность

В неориентированном графе две вершины либо связаны (если существует соединяющая их цепь), либо не связаны. В ориентированном графе отношение связанности узлов несимметрично, а потому определение связности отличается.

Пусть G (X, V) – орграф, x1 и x2 – его узлы. Два узла – x1 и x2 – сильно связаны в орграфе G, если существует путь (ориентированная цепь) как из x1 в x2, так и из x2 в x1. Два узла – x1 и x2 – односторонне связаны в орграфе G, если существует путь либо из x1 в x2, либо из x2 в x1. Два узла – x1 и x2 – слабо связаны в орграфе G, если они связаны в графе G', полученном из G забыванием ориентации дуг.

Если все вершины в орграфе сильно (односторонне, слабо) связаны, то орграф называется сильно (односторонне, слабо) связным. Сильная связность влечет за собой одностороннюю, которая влечет слабую связность. Обратное, разумеется, неверно.

На рис. 21 показаны диаграммы сильно, односторонне и слабо связных орграфов.

Рис. 21. Сильная (а), односторонняя (б) и слабая (в) связность

Компоненты сильной связности

Компонента сильной связности (КСС) орграфа G – это его максимальный сильно связный подграф.

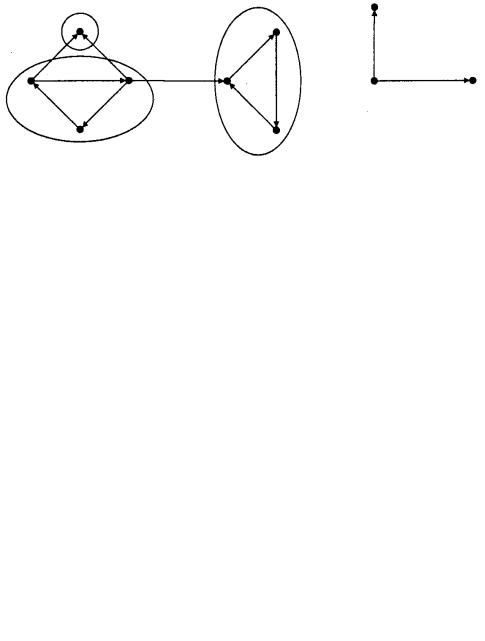
Каждый узел орграфа принадлежит только одной КСС. Если узел не связан сильно с другими, то считается, что он сам образует КСС. Конденсацией G* орграфа G (графом Герца, фактор-графом) называется орграф, который получается стягиванием в один узел каждой КСС орграфа G (рис. 22).

Фактор-граф не содержит контуров.

Рис. 22. Диаграммы орграфа (а) и его конденсации (б)

Данный алгоритм, основанный на методе поиска в глубину, находит все компоненты сильной связности орграфа.

Вход: орграф G (X, V), заданный списками смежности Г(x).

Выход: список С компонент сильной связности, каждый элемент которого есть список узлов, входящих в компоненту сильной связности.

Основная работа выполняется рекурсивной процедурой без параметров КСС, которая использует стек Т для хранения просматриваемых узлов. Процедура КСС выделяет все компоненты сильной связности, достижимые из узла, выбранного в основном алгоритме.

if T = Ø then return

end if

x := top Т {x – верхний элемент стека} if Г[x] X = Ø then

C := C M[x]

X := X – x x Т

КСС else

for u Г[x] do if v[u] = 0 then