ГЛАВА 1

ОСНОВНЫЕ ПОЛОЖЕНИЯ ТЕОРИИ ГРАФОВ

Среди дисциплин и методов дискретной математики теория графов и особенно алгоритмы на графах находят наиболее широкое применение в программировании. Между понятием графа и понятием бинарного отношения имеется глубокая связь – можно сказать, что это равнообъемные понятия. Тем не менее графам оказывается заметное предпочтение при изучении дискретной математики и программирования, поскольку теория графов предоставляет очень удобный язык для описания моделей. Этот тезис можно пояснить следующей аналогией. Понятие отношения также можно полностью выразить через понятие множества. Однако независимое определение понятия отношения удобнее. Введение специальных терминов и обозначений упрощает изложение теории и делает ее более понятной. То же относится и к теории графов. Система специальных терминов и обозначений позволяет доступно описывать ее сложные процессы и этапы функционирования.

Название «граф» подразумевает наличие графической интерпретации. Это позволяет наглядно определить суть дела на интуитивном уровне, дополняя и украшая утомительные текстовые доказательства и сложные формулы.

Разные авторы предлагают множество интерпретаций теории графов.

В частности, она служит для решения задач, рассмотренных ниже и подобных им.

1. Задача о трех домах и трех колодцах. Три дома и три колодца располо-

жены на плоскости. Требуется провести от каждого дома к каждому колодцу дорожку так, чтобы они не пересекались (рис. 1).

Рис. 1. Задача о трех домах и трех колодцах

2. Задача о Кенигсбергских мостах. На рис. 2 представлена центральная часть города Кенигсберг (ныне Калининград), включающая два берега реки Преголя, два острова на ней и семь соединяющих их мостов. Задача состоит в том, чтобы обойти все четыре участка берега, пройдя по каждому мосту один раз, и вернуться в исходную точку.

Рис. 2. Задача о Кенигсбергских мостах

3. Задача о четырех красках. Разделение плоскости на неперекрывающиеся области называется картой. Области на карте называются соседними, если они имеют общую границу. Задача состоит в раскрашивании карты таким образом, чтобы никакие две соседние области не были закрашены одним цветом (рис. 3).

Рис. 3. Задача о четырех красках

С конца XIX века известна гипотеза, что для выполнения этой задачи достаточно четырех красок. В 1976 году К. Аппель и В. Хейкен опубликовали решение задачи о четырех красках, которое базировалось на переборе вариантов с помощью компьютера. Проверить вручную полученное решение невозможно

– объем перебора выходит далеко за рамки человеческих возможностей.

Таким образом, граф позволяет обозначать любые объекты и любые связи между ними. В простом случае подразумевается, что все ребра графа отражают связи одной природы. Например, граф сети воздушных трасс в секторе района УВД показывает связи между пунктами обязательного донесения участков ВТ. В другом случае в виде графа можно изобразить информационные связи между объектами, например, линии связи между аэродромными службами и диспетчерскими пунктами. Граф может служить моделью отношения «часть – целое» и показывать, из чего состоит тот или иной агрегат, отношения родственных связей между объектами (генеалогическое дерево суть тот же граф) и др.

Важно учитывать, что граф не является масштабным изображением реальной системы, то есть здесь не отображаются реальные расстояния между объектами.

Граф позволяет наглядно отобразить взаимосвязи объектов реальной системы, кроме этого с помощью графовых моделей в различных предметных областях решается множество задач.

Задачи планирования потока в транспортной сети относятся к одному из возможных классов задач, решаемых с помощью графов.

1.1. Основное определение

Граф представляет собой модель системы объектов, связанных между собой определенными отношениями. Графом G(X, V) называется совокупность двух множеств – непустого множества X (множества вершин) и множества V двухэлементных подмножеств множества X (V – множество ребер),

Любое множество V двухэлементных подмножеств множества X определяет симметричное бинарное отношение на множестве X. Поэтому можно считать, что

VX X , V V 1,

итрактовать ребро не только как множество {x1, x2}, но и как пару (x1, x2). Число вершин графа G обозначим p, а число ребер – q:

Если необходимо явно упомянуть числовые характеристики графа, то следует сказать: (p, q) – граф.

В модели системы объектов им соответствуют вершины графа, связям – ребра (дуги) графа. Изображается граф в виде множества точек (вершин), соединенных линиями (ребрами или дугами в ориентированном графе).

Математически граф G задается в следующем виде:

G (X, V),

где X = {х1, х2, …, хn} – множество вершин (n – количество вершин, нумерация, как правило, произвольная);

V = {v1, v2, ..., vm} - множество ребер (m – количество ребер – может отличаться от количества вершин, нумерация, как правило, произвольная).

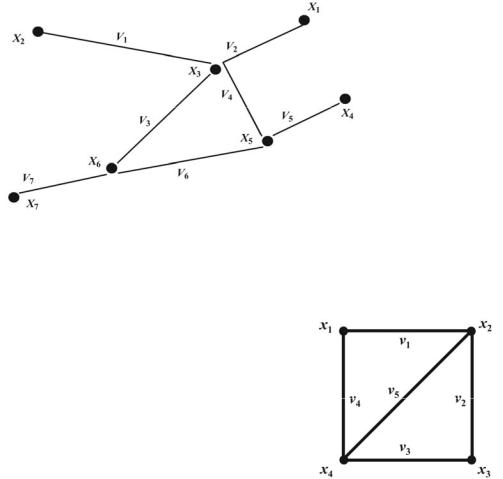
Ребра можно записать и в таком виде: v(х1, х2) – ребро между вершинами х1 и х2 или вообще как пару (х1, х2). В данном пособии для упрощения записи часто будет использован первый вариант. Пример графа представлен на рис. 4.

Рис. 4. Пример графа

Обычно граф изображают диаграммой: вершины – точками (или кружками), ребра – линиями.

На рис. 5 приведен пример диаграммы графа, имеющего четыре вершины и пять ребер. В этом графе вершины x1 и x2, x2 и x3, x3 и x4, x2 и x4 смежны, а