ГЛАВА 2

СВЯЗНОСТЬ ГРАФОВ

Связность является одним из немногих понятий, которые не распространяются непосредственно с графов на другие родственные объекты и требуют отдельного определения и рассмотрения в каждом случае.

2.1. Объединение графов и компоненты связности

Связный граф – граф, содержащий ровно одну компоненту связности. Это означает, что между любой парой вершин этого графа существует по крайней мере один путь.

Теорема. Граф связен тогда и только тогда, когда его нельзя представить в виде объединения двух графов.

Несвязный граф всегда можно представить как объединение связных компонент. Их можно рассматривать независимо. Поэтому во многих случаях можно без ограничения общности предполагать, что рассматриваемый граф связен.

Точки сочленения, мосты и блоки

Вершина графа называется точкой сочленения, или разделяющей вершиной, если ее удаление увеличивает число компонент связности. Мостом называется ребро, удаление которого увеличивает число компонент связности. Блоком называется связный граф, не имеющий точек сочленения.

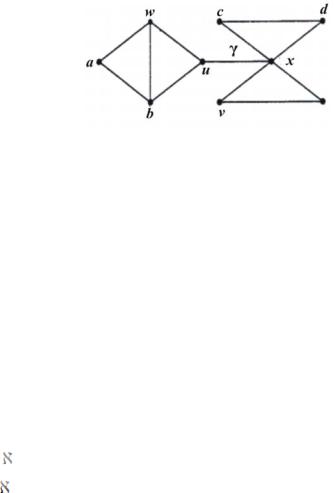
Вграфе, диаграмма которого представлена на рис.15:

1)вершины u, x – точки сочленения, других точек сочленения нет;

2)ребро γ – мост, других мостов нет;

блоки, других блоков нет.

Рис. 15. Точки сочленения, мосты и блоки

Лемма. В любом нетривиальном графе есть, по крайней мере, две вершины, которые не являются точками сочленения.

2.2. Вершинная и реберная связность

Если сравнить рис. 6 и 15, то возникает естественное впечатление, что связный граф может быть «более» или «менее» связен. Вершинной связностью графа G (обозначается (G)) называется наименьшее число вершин, удаление которых приводит к несвязному или тривиальному графу.

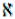(Кp) = p – 1, если Кp – полный граф. Граф G называется п-связным, если (G) = п.

Реберной связностью графа G (обозначается (G)) называется наименьшее число ребер, удаление которых приводит к несвязному или тривиальному графу.

(Кр) = р – 1, если Кр – полный граф.

Граф тем более связен (при использовании различных мер связности), чем больше существует различных цепей, соединяющих одну вершину с другой, и тем менее связен, чем меньше нужно удалить промежуточных вершин, чтобы отделить одну вершину от другой.

2.3. Непересекающиеся цепи и разделяющие множества

Пусть G (X, V) – связный граф, u и x – две его несмежные вершины. Две цепиu, x называются вершинно-непересекающимися, если у них нет общих вершин, отличных от u и x. Две цепи u, x называются реберно-непересекающимися, если у них нет общих ребер. Если две цепи вершинно не пересекаются, то они также не пересекаются реберно. Обозначим через P(u, x) множество вершиннонепересекающихся цепей u, x .

Множество S вершин (и/или ребер) графа G разделяет две вершины u и x, если они принадлежат разным компонентам связности графа G–S. Разделяющее множество ребер называется разрезом. Разделяющее множество вершин для и и x обозначим S(u, x).

Для заданных вершин и и x множества Р(u, x) и S(u, x) можно выбирать различным образом.

Из определений следует, что любое множество P(u, x) вершинно-непересе- кающихся цепей обладает тем свойством, что

u, x {u, x},

(u, x) P(u, x)

а любое разделяющее множество вершин S(u, x) обладает тем свойством, что

G S G1 G2 & x G1 & u G2 .

Если u и x принадлежат разным компонентам связности графа G, то |P(u, x)| = 0 и |S(u, x)| = 0. Поэтому без ограничения общности можно считать, что G – связный граф.

В графе, диаграмма которого представлена на рис. 16, можно выбрать множества вершинно-непересекающихся путей:

P1 { u, a, d, x , u, b, v, x } и P2 { u, b, d, x , u, c, v, x }.

Заметим, что путь u, c, b, d, x образует множество Р3 вершинно-непере- секающихся путей, состоящее из одного элемента.

Множества вершин S1 = {а, b, с} и S2 = {d, v} являются разделяющими для вершин u и x.

Рис.16. Вершинно-непересекающиеся пути и разделяющие множества вершин

2.4. Теорема Менгера

Теорема Менгера представляет собой весьма общий факт, который в разных формулировках встречается в различных областях математики.

Теорема Менгера в «вершинной форме»

Пусть u и x – несмежные вершины в графе G. Наименьшее число вершин во множестве, разделяющем u и x, равно наибольшему числу вершиннонепересекающихся простых u, x -цепей:

max |P(u, x)| = min |S(u, x)|.

Пусть G – связный граф, и вершины u и v не смежны. Обозначим P := P(u, x), S := S(u, x). Из этого следует, что |P| |S|. Действительно, любая u, x -цепь проходит через S. Если бы |P| > |S|, то S включало бы вершину, принадлежащую более чем одной цепи из P, что противоречит выбору Р. Таким образом,

P ( S ( P S )) .

Следовательно, max |P| min |S|. Утверждение теоремы состоит в том, что в любом графе существуют такие P и S, при которых достигается равенство |P| = |S|.

Доказательство. Пусть G – связный граф, u и x – несмежные вершины. Совместная индукция по р и q. База: наименьший граф, удовлетворяющий условиям теоремы, состоит из трех вершин: u, w, x – и двух ребер: (u, w) и (w, x). В таком графе P(u, x) = { u, w, x } и S(u, x) = {w}.

Таким образом, |P(u, x)| = |S(u, x)| = 1.

Пусть утверждение теоремы верно для всех графов с числом вершин меньше р и/или числом ребер меньше q. Рассмотрим граф G с р-вершинами и q-ребрами. Пусть (u, x) X, причем u, x – не смежны, а S – некоторое наименьшее множество вершин, разделяющее u и x.

Обозначим n := |S|. Рассмотрим три случая:

1. Пусть в S есть вершины, не смежные с u и не смежные с x. Тогда граф G–S состоит из двух нетривиальных графов G1 и G2. Образуем два новых графа Gu и Gx, стягивая нетривиальные графы G1 и G2 к вершинам u и x соответственно

(рис. 17):

Gu := G/G1, Gx := G/G2.

Рис. 17. К доказательству теоремы Менгера, случай 1

S по-прежнему является наименьшим разделяющим множеством для u и x как в Gu, так и в Gx. Так как G1 и G2 нетривиальны, то Gu и Gx имеют меньше вершин и/или ребер, чем G. Следовательно, по индукционному предположению в Gu и в Gx имеется n вершинно-непересекающихся простых цепей. Комбинируя отрезки этих цепей от u до S и от S до x, получаем n вершиннонепересекающихся простых цепей в G.

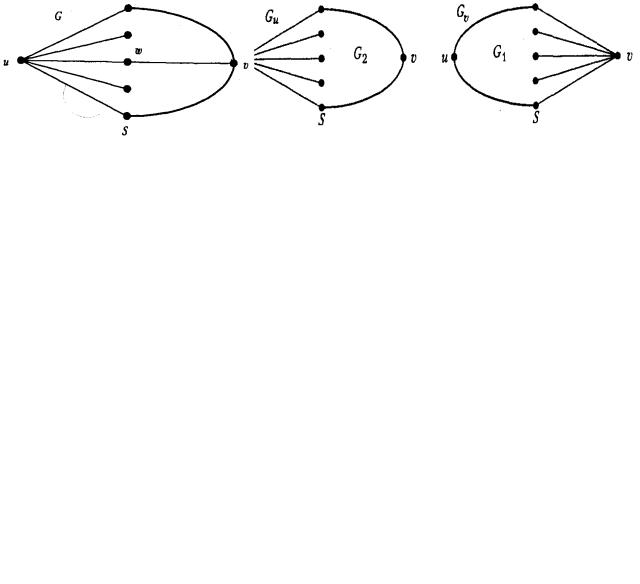
2. Пусть все вершины S смежны с u или с x (для определенности условимся считать, что с u), и среди них есть вершина w, смежная одновременно с u и с x

(рис. 18).

Рис. 18. К доказательству теоремы Менгера, случай 2

Рассмотрим граф G' : = G – w. В нем S – w – разделяющее множество для и и x, причем наименьшее. По индукционному предположению в G' имеется S w n 1 вершинно-непересекающихся простых цепей. Добавим к ним цепь u, w, x , которая является простой и вершинно не пересекается с остальными. Таким образом, G содержит n вершинно-непересекающихся простых цепей.

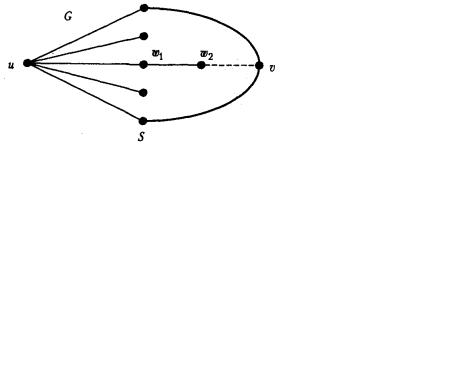
3. Пусть все вершины S смежны с и или с x (для определенности условимся считать, что с и), и среди вершин S нет вершин, смежных одновременно с вершиной u и с вершиной x. Рассмотрим кратчайшую u, x -цепь u, w1, w2 , ..., x , w1 S, w2 = x (рис. 19):

Рис. 19. К доказательству теоремы Менгера, случай 3

Рассмотрим граф G ' := G/{w1, w2}, полученный из G склейкой вершин w1 и w2 в вершину w1. Имеем w2 S, в противном случае цепь u, w2 , ..., x была бы еще более короткой. Следовательно, в графе G ' множество S по-прежнему является наименьшим, разделяющим и и x, и граф G ' имеет по крайней мере на одно ребро меньше. По индукционному предположению в G ' существуют n вершинно-непересекающихся простых цепей. Но цепи, которые не пересекаются в G', не пересекаются и в G. Таким образом, получаем n вершиннонепересекающихся простых цепей в G.

Варианты теоремы Менгера

Комбинируя вершинно- и реберно-непересекающиеся цепи, разделяя не отдельные вершины, а множества вершин, используя инварианты и , можно сформулировать и другие утверждения, подобные теореме Менгера.