Эксцентриситетом v(x) вершины x в связном графе G(X, V) называется максимальное расстояние от вершины x до других вершин графа G:

def

v(x) max d(х,и) .

u X

Наиболее эксцентричные вершины – это концы диаметра.

Радиусом R(G) графа G называется наименьший из эксцентриситетов вершин:

def

R(G) min v(х) .

x X

Вершина x называется центральной, если ее эксцентриситет совпадает с радиусом графа, v(x) = R(G). Множество центральных вершин называется центром графа и обозначается C(G):

def

C(G) {x X v(x) R(G)}.

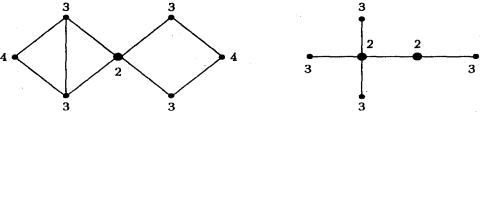
На рис. 10 указаны эксцентриситеты вершин и центры двух графов. Вершины, составляющие центр, выделены жирными точками.

Рис. 10. Эксцентриситеты вершин и центры графов

1.6. Виды графов

Тривиальный и полный графы

Граф, состоящий из одной вершины, называется тривиальным. Граф, состоящий из простого цикла с k-вершинами, обозначается Ck.

Например, C3 – треугольник.

Граф, в котором любые две вершины смежны, называется полным. Полный граф с p-вершинами обозначается Kp и имеет максимально возможное число ребер:

p( p 1) . 2

Полный подграф (некоторого графа) называется кликой (этого графа).

Двудольные графы

Граф G(X, V) называется двудольным (или биграфом, или четным графом), если множество X может быть разбито на два непересекающихся множества: X1 и X2 (X1 X2 = X, X1 X2 = ), причем всякое ребро из V инцидентно вершине из X1 и вершине из X2 (т. е. соединяет вершину из X1 с вершиной из X2). Множества X1 и X2 называются долями двудольного графа. Если двудольный граф содержит все ребра, соединяющие множества X1 и X2, то он называется полным двудольным графом. Если |X1| = т и |X2| = n, то полный двудольный граф обозначается Km,n. Например, на рис. 6 приведена диаграмма графа К3,3.

Граф является двудольным тогда и только тогда, когда все его простые циклы имеют четную длину.

Направленные орграфы и сети

Если в графе ориентировать все ребра, то получится орграф, который назы-

вается направленным (или антисимметричным).

Вантисимметричном орграфе не может быть «встречных» дуг (u, x) и (x, u),

ав произвольном такое допустимо.

Направленный орграф, полученный из полного графа, называется турниром. Объясним происхождение термина. Рассмотрим спортивное соревнование для пар участников (или пар команд), где не предусматривается ничья. Пометим вершины орграфа участниками и проведем дуги от победителей к побежденным. В данном случае турнир в контексте теории графов – это как раз ре-

зультат однокругового турнира в спортивном смысле.

Если в орграфе полустепень захода некоторого узла равна нулю (т. е. d+(x) = 0), то такой узел называется источником; если нулю равна полустепень исхода (т. е. d–(x) = 0), то узел называется стоком. Направленный слабосвязный орграф с одним источником и одним стоком называется сетью.

1.7. Графы и отношения

Любой орграф G (X, V) с петлями, но без кратных дуг, задает бинарное отношение V на множестве X и обратно. Пара элементов принадлежит отношению (a, b) V X × X тогда и только тогда, когда в графе G есть дуга (a, b). Полный граф соответствует универсальному отношению. Граф (неориентированный) соответствует симметричному отношению. Дополнение графов есть дополнение отношений. Изменение направления всех дуг соответствует обратному отношению и т. д.

Отступление. Таким образом, имеется полная аналогия между орграфами и бинарными отношениями – фактически, это один и тот же класс объектов, только описанный разными средствами. Отношения (в частности, функции) являются базовым средством для построения подавляющего большинства математических моделей, используемых при решении практических задач. С другой стороны, графы допускают наглядное представление в виде диаграмм. Этим обстоятельством объясняется широкое использование диаграмм различного вида (которые суть представления графов или родственных объектов) при кодировании и особенно при проектировании в программировании.

Достижимость и частичное упорядочение

В качестве примера связи между орграфами и бинарными отношениями рассмотрим отношения частичного порядка с точки зрения теории графов. Узел и в орграфе G (X, V) достижим из узла x, если существует путь из x в и. Путь из x в и обозначим x, u . Отношение достижимости можно представить следующей матрицей:

Т: array [1...p, 1...p] of 0...1,

где T[i, j] = 1, если узел xj достижим из узла xi, и T[i, j] = 0, если узел xj не достижим из узла xi. Рассмотрим отношение строгого частичного порядка, которое характеризуется следующими аксиомами:

С отношением строгого частичного порядка X X можно сопоставить орграф G (X, V), в котором a b (a,b) V .

Теорема 1. Если отношение V есть строгое частичное упорядочение, то орграф G (X, V) не имеет контуров.

Доказательство (от противного). Пусть в G есть контур. Рассмотрим любую дугу (а, b) в этом контуре. Тогда имеем а > b, но b > а по транзитивности, что противоречит антисимметричности упорядочения.

Теорема 2. Если орграф G (X, V) не имеет контуров, то отношение достижимости есть строгое частичное упорядочение.

Доказательство.

–Антирефлексивность. Нет контуров, следовательно, нет петель.

–Транзитивность. Если существуют пути из x в w и из w в и, то существует

ипуть из x в u.

–Антисимметричность (от противного). Пусть u, x (u x & x u) , т. е.

существует путь x, u из x в и и путь u, x из и в x. Следовательно, существует контур вида x, u + u, x , что противоречит условию.

Теорема 3. Если орграф не имеет контуров, то в нем есть узел, полустепень захода которого равна 0.

Доказательство (от противного). Пусть такого узла нет, тогда для любого узла найдется узел, из которого есть дуга в данный узел. Следовательно, имеем контур против направления стрелок.

Транзитивное замыкание

Если V – бинарное отношение на X, то транзитивным замыканием V+ на X будет отношение достижимости на орграфе G (X, V).

Теорема. Пусть М – матрица смежности орграфа G (X, V). Тогда Mk[i, j] = 1 в том и только в том случае, если существует путь длиной k из узла xi в узел xj.

Доказательство. Индукция по k. База: k = 1, М1 = М – пути длины 1. Пусть Мk-1 содержит пути длины k – 1. Тогда

p

M k [i, j] V(M k 1[i,l] & M[l, j],

l 1