1.2. Орграфы, псевдографы, мультиграфы и гиперграфы

Часто рассматриваются следующие родственные графам объекты:

1. Если элементами множества V являются упорядоченные пары (т. е. V X X ), то граф называется ориентированным (или орграфом). В этом случае элементы множества X называются узлами, а элементы множества V – дугами.

2.Если элементом множества V может быть пара одинаковых (не различных) элементов X, то такой элемент множества V называется петлей, а граф называется графом с петлями (или псевдографом).

3.Если V является не множеством, а мультимножеством, содержащим некоторые элементы по несколько раз, то эти элементы называются кратными ребрами, а граф называется мультиграфом.

4.Если элементами множества V являются не обязательно двухэлементные,

алюбые (непустые) подмножества множества X, то такие элементы множества V называются гипердугами, а граф называется гиперграфом.

Если задана функция F: X → М и/или F: V → М, то множество М называется множеством пометок, а граф называется помеченным (или нагруженным). В качестве множества пометок обычно используются буквы или целые числа. Если функция F инъективна, то есть разные вершины (ребра) имеют разные пометки, то граф называется нумерованным.

1.3.Смежность

Пусть x1, x2 – вершины, v = (x1, x2) – соединяющее их ребро. Тогда вершина x1 и ребро v инцидентны, ребро v и вершина x2 также инцидентны. Два ребра, инцидентные одной вершине, называются смежными; две вершины, инцидентные одному ребру, также называются смежными. Множество вершин, смеж-

ных с вершиной x, называется множеством смежности (или окрестностью)

вершины x и обозначается Г+(x):

Если не оговорено противное, то символ Г без индекса подразумевает Г+, то есть саму вершину в окрестность не включают.

Очевидно, что u Г(x) x Г(u). Если A X – множество вершин, то Г(А)

– множество всех вершин, смежных с вершинами из A:

def

Г( A) {u X x A(u Г(x))} Г(x) .

x A

Отношение смежности является в некотором смысле определяющим для графов и подобных им объектов. При этом следует учитывать особенности каждого типа объектов. В орграфе вершина x смежна с вершиной u, если существует дуга (u, x). При этом вершина и может быть не смежна с вершиной x. Отношение смежности в графе симметрично, а в орграфе оно вовсе не обязано быть симметричным. В графе обычно считают отношение смежности рефлексивным, то есть полагают, что вершина смежна сама с собой. В псевдографе, напротив, вершину не считают смежной с собой, если у нее нет петли. В гиперграфе две вершины считаются смежными, если они принадлежат одному гиперребру. В гиперорграфе гипердуга обычно проводится из одного узла во множество узлов (возможно, пустое). В таком случае отношение смежности оказывается уже не бинарным отношением на X, а отношением из X в 2X. Эти и подобные естественные вариации определений обычно считают ясными из контекста.

Выражение «граф G (X, V)» означает неориентированный непомеченный граф без петель и кратных ребер с множеством вершин X и множеством ребер V.

1.4. Изоморфизм графов

Два графа, G1(X1, V1) и G2(X2, V2), изоморфны (обозначается G1 ~ G2, или G1 = G2), если существует биекция h: X1 → X2, сохраняющая смежность

v1 = (u, x) V1 v2 = (h(u), h(x)) V2.

Изоморфизм графов – отношение эквивалентности – обладает всеми необходимыми свойствами:

Рефлексивность G ~ G, где требуемая биекция есть тождественная функция. Симметричность, если G1 ~ G2 с биекцией h, то G2 ~ G1 с биекцией h-1. Транзитивность, если G1 ~ G2 с биекцией h и G2 ~ G3 с биекцией g, то G1 ~ G3

с биекцией g o h.

Три внешне различные диаграммы, приведенные на рис. 6, являются диаграммами одного и того же графа K3,3.

Рис. 6. Диаграммы изоморфных графов

Числовая характеристика, одинаковая для всех изоморфных графов, называется инвариантом графа. Так, p(G) и q(G) – инварианты графа G. Неизвестно ни одного простого набора инвариантов, определяющих граф с точностью до изоморфизма.

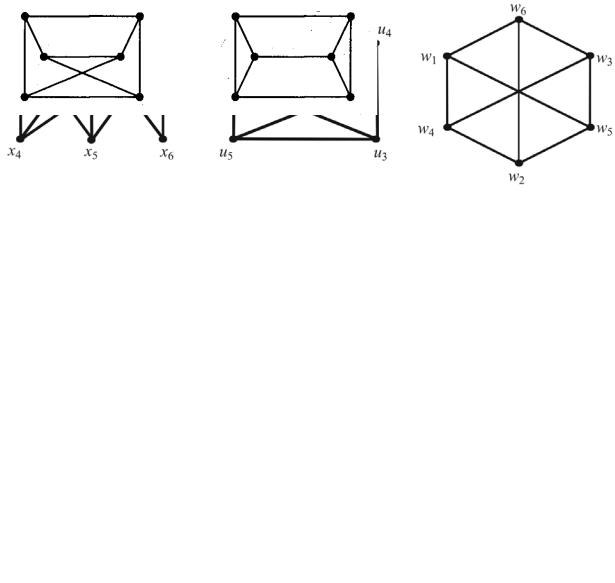
Количество вершин, ребер и количество смежных вершин для каждой вершины не определяют граф даже в простейших случаях. На рис. 7 представлены диаграммы графов, у которых указанные инварианты совпадают, но графы при этом не изоморфны.

Рис. 7. Диаграммы неизоморфных графов с совпадающими инвариантами

1.5. Элементы графов

Подграфы

Граф G' (X', V') называется подграфом (или частью) графа G (X, V) (обозначается G' G), если X' X & V' V. Если X' = X, то G' называется остовным подграфом G. Если X' X & V' V & (X' ≠ X V' ≠ V), то граф G' называется собственным подграфом графа G. Подграф G' (X', V') называется правильным подграфом графа G (X, V), если G' содержит все возможные ребра G:

u, x X' ((u, x) V (u, x) V' ) .

Правильный подграф G' (X', V') графа G (X, V) определяется подмножеством вершин X'.

Иногда подграфами называют только правильные подграфы, а неправильные подграфы называют иэграфами.

Валентность

Количество ребер, инцидентных вершине x, называется степенью (или валентностью) вершины x и обозначается d(x):

x X (0 d(x) p 1), d(x) Г (x) .

Таким образом, степень d(x) вершины x совпадает с количеством смежных с ней вершин. Количество вершин, не смежных с x, обозначают d(x). Ясно, что

x X (d(x) d(x) p 1) .

Обозначим минимальную степень вершины графа G через δ(G), а макси-

мальную – через ∆(G):

Ясно, что δ(G) и ∆(G) являются инвариантами. Если степени всех вершин равны k, то граф называется регулярным степени k:

(G) (G) k, x X (d (x) k).

Степень регулярности обозначается, как r(G). Для нерегулярных графов r(G) не определено.

На рис. 8 приведена диаграмма регулярного графа степени 3. На рис. 7 – диаграммы двух регулярных, но неизоморфных графов степени 3.

Если степень вершины равна нулю (т. е. d(x) = 0), то вершина называется изолированной. Если степень вершины равна

единице (т. е. d(x) = 1), то вершина называется концевой, или висячей. Для орграфа число дуг, исходящих из узла x, называется полустепенью исхода, а число входящих – полустепенью за-

хода. Обозначаются эти числа, соответственно, d –(x) и d+(x).

Маршрутом в графе называется чередующаяся последовательность вершин и ребер, начинающаяся и кончающаяся вершиной, (x0, v1, x1, v2, x2, ..., vk, xk), в которой любые два соседних элемента инцидентны, причем однородные элементы (вершины, ребра) через один смежны или совпадают.

Это определение подходит также для псевдо-, мульти- и орграфов. При этом в графе (орграфе) достаточно указать только последовательность вершин (узлов) или только последовательность ребер (дуг).

Если x0 = xk, то маршрут замкнут, иначе – открыт.

Если все ребра различны, то маршрут называется цепью. Если все вершины (а значит, и ребра) различны, то маршрут называется простой цепью. В цепи x0, v1, ..., vk, xk вершины x0 и xk называются концами цепи. Говорят, что цепь с концами u и x соединяет вершины u и x. Цепь, соединяющая вершины u и x, обозначается u, x . Если требуется указать граф G, которому принадлежит цепь, то добавляют индекс: u, x G . Нетрудно показать, что если есть какаялибо цепь, соединяющая вершины u и x, то есть и простая цепь, соединяющая эти вершины.

Замкнутая цепь называется циклом; замкнутая простая цепь – простым циклом. Число циклов в графе G обозначается z(G). Граф без циклов называется ациклическим. Для псевдографов обычно особо оговаривается, считаются ли петли циклами.

Для орграфов цепь называется путем, а цикл – контуром. Путь в орграфе из узла и в узел x обозначается u, x .

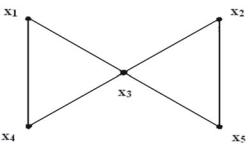
Рассмотрим примеры маршрутов, цепей и циклов диаграммы графа, приведенной на рис. 9:

Связность

Две вершины в графе связаны, если существует соединяющая их (простая) цепь. Граф, в котором все вершины связаны, называется связным. Отношение связанности вершин является эквивалентностью. Классы эквивалентности по отношению связанности называются компонентами связности графа. Число компонентов связности графа G обозначается k(G). Граф G является связным тогда и только тогда, когда k(G) = 1. Если k(G) > 1, то G – несвязный граф. Граф, состоящий только из изолированных вершин (в котором k(G) = p(G) и r(G) = 0),

называется вполне несвязным.

Длина маршрута, расстояние между вершинами, ярусы и диаметр графа

Длиной маршрута называется количество ребер в нем (с учетом повторений). Если маршрут М = x0, v1, x1, v2, x2, ..., vk, xk, то длина М равна k (обозначается М k ).

Расстоянием между вершинами u и x (обозначается d(u, x)) называется длина кратчайшей цепи u, x , а сама кратчайшая цепь называется геодезической:

def

d(u, x) min u, x .

{ u, x }

Если для любых двух вершин графа существует единственная геодезическая цепь, то граф называется геодезическим.

Множество вершин, находящихся на заданном расстоянии n от вершины x (обозначается D(x, n)), называется ярусом:

def

D(x, n) {u X d(x,u) n}.

Множество вершин X всякого связного графа однозначно разбивается на ярусы относительно данной вершины.

Диаметром графа G называется длиннейшая геодезическая цепь. Длина диаметра обозначается D(G):

def

D(G) max d(u, x) .

u, x X