т. Е. путь длины k из узла i в узел j существует тогда и только тогда, когда найдется узел l, такой, что существует путь длины k – 1 из i в l и дуга (l, j), т. е.

i, j i, j k l ( i,l ( i,l k 1) & (l, j) V ) .

Если T – матрица достижимости, то очевидно, что

p 1

Т V M k .

k 1

Трудоемкость прямого вычисления по этой формуле составляет O(р4). Матрица достижимости Т может быть вычислена по матрице смежности М алгоритмом Уоршалла за O(р3).

1.8. Способы представления графов в памяти компьютера

Требования к представлению графов

Любую рассматриваемую задачу для моделей реальных систем не всегда возможно решать без автоматизации вычислений. Методы теории графов позволяют для решения задач использовать ЭВМ. Однако при этом необходимо представить граф в памяти компьютера.

Известны различные способы представления графов в памяти компьютера, которые различаются объемом занимаемой памяти и скоростью выполнения операций над графами. Представление выбирается, исходя из потребностей конкретной задачи. Ниже приведены четыре наиболее часто используемых представления с указанием характеристики n(p, q) – объема памяти для каждого представления. В данном случае p – число вершин, a q – число ребер.

Значение характеристики n(p, q) указывается с помощью символа О, который обозначает совпадение по порядку величины (или равенство с точностью до мультипликативной константы с). Применительно к измерению занимаемой памяти использование символа О связано с тем, что память может быть измерена в битах, байтах, машинных словах или иных единицах. Коэффициент c при этом меняется, а порядок величины остается.

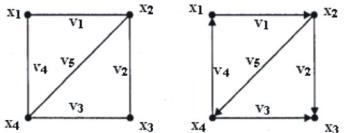
Представления иллюстрируются на конкретных примерах графа G и орграфа D, диаграммы которых представлены на рис. 11.

аб

Рис. 11. Диаграммы графа (а) и орграфа (б), используемых в качестве примеров представлений

Конструирование структур данных для представления в программе объектов математической модели – основа искусства практического программирования. На практике используются, как правило, некоторые комбинации или модификации представлений, общее число которых необозримо. Но все они, так или иначе, основаны на базовых идеях.

Матричные представления

Базовыми формами представления графов в памяти компьютера являются матрица смежности и матрица инциденций.

Матрица смежности представляет собой таблицу, в которой номера столбцов и строк означают номера вершин графа. На пересечении строк и столбцов ставится 1, если вершины соединены ребром в графе, и 0, если не соединены.

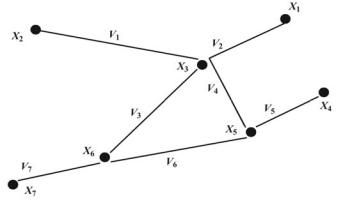
В матрице инциденций номера строк – номера вершин, а номера столбцов – номера ребер (дуг). На их пересечении ставится 1, если ребро и вершина инцидентны (т. е. ребро соединено с данной вершиной). Для графа (рис. 12) матрицы смежности и инциденций показаны ниже. В общем случае матрица инциденций необязательно квадратная.

Рис. 12. Пример графа

Матрица смежности. Представление графа с помощью квадратной булевой матрицы

М: array [1...p, 1...p] of 0...1,

отражающей смежность вершин, называется матрицей смежности, где

Матрица смежности графа симметрична относительно главной диагонали, поэтомудостаточнохранитьтольковерхнюю(илинижнюю) треугольнуюматрицу.

Матрица инциденций. Представление графа с помощью матрицы:

H: array [1...p, 1...q] of 0...1,

для орграфа

H: array [1...p, 1...q] of 0...1,

отражающей инцидентность вершин и ребер, называется матрицей инциденций, где для неориентированного графа

1, если вершина xi инцидентна ребру v j ,

H[i, j]

0, в противном случае,

Для связных графов q > p, поэтому матрица смежности несколько компактнее матрицы инциденций.

Списки смежности

Представление графа с помощью списочной структуры, отражающей смежность вершин и состоящей из массива указателей

Г: array [1...p] of ↑ N

на списки смежных вершин, где элемент списка представлен структурой

N = record x: 1...p, n: ↑ N end record,

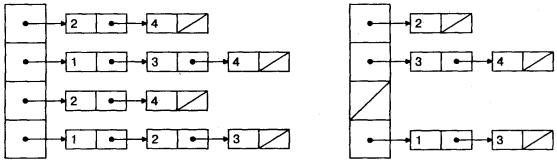
называется списком смежности (рис. 13). В случае представления неориентированных графов списками смежности n(p, q) = O(p + 2q), а в случае ориентированных графов n(p, q) = O(p + q). Массив Г также можно представить списком.

Рис. 13. Списки смежности для графа G (а) и орграфа D (б)

Массив ребер

Представление графа с помощью массива структур

V: array [1...q] of record b, v: 1...p end record,

отражающего список пар смежных вершин (или, для орграфов, узлов), называет-

ся массивом ребер (массивом дуг). Для массива ребер (или дуг) n(p, q) = O(2q).

Для представления графов с изолированными вершинами может понадобиться хранить еще и число p, если только система программирования не позволяет извлечь это число из массива структур V.

Представление графов с помощью массива ребер (дуг) выглядит следующим образом (для графа G слева, а для орграфа D справа):

Указанные представления пригодны для графов и орграфов, а после некоторой модификации – и для псевдографов, мультиграфов и гиперграфов.

Обходы графов

Обход графа – некоторое систематическое перечисление его вершин (и/или ребер). Наибольший интерес представляют обходы, использующие локальную информацию (списки смежности). Среди всех обходов наиболее известны поиск в ширину и в глубину. Алгоритмы поиска в ширину и в глубину лежат в основе многих конкретных алгоритмов на графах.

АЛГОРИТМ ПОИСКА В ШИРИНУ И В ГЛУБИНУ

Вход: граф G (X, V), представленный списками смежности Г. Выход: последовательность вершин обхода.

For w Г(u) do

If x[w] = 0 then

w → T {помещаем w в структуру данных Т...} γ[w] := 1 {... и отмечаем вершину w}

End if

End for Until T = .

Если в данном алгоритме структуры данных T – это стек (LIFO – Last In First Out), то обход называется поиском в глубину. Если Т – это очередь (FIFO – First In First Out), то обход называется поиском в ширину.

Протоколы поиска в глубину и в ширину для графа, диаграмма которого приведена на рис. 14, выглядzт следующим образом:

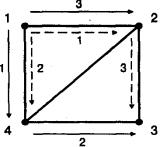
Предполагается, что начальной является вершина 1. Слева представлен протокол поиска в глубину, справа – в ширину. На рис. 14 сплошные стрелки с номерами рядом с ребрами показывают движение по графу при поиске в глубину, а пунктирные – в ширину.

Если граф G связен (и конечен), то при поиске в ширину и в глубину обходят все вершины

по одному разу. Рис. 14. Диаграмма графа обхода в ширину и в глубину

Следствие 1. Пусть (u1, ..., ui, ..., uj, ..., uр) – обход (т. е. последовательность вершин) при поиске в ширину. Тогда

i j (d(u1 ,ui ) (u1 ,u j )) .

Другими словами, расстояние текущей вершины от начальной является монотонно возрастающей функцией времени поиска в ширину, вершины обходятся в порядке возрастания расстояния от начальной вершины.

Следствие2. Пусть (u1, ..., ui, ..., uр) – обход при поиске в глубину. Тогда

i i (d(u1 ,ui ) i p) .

Другими словами, время поиска в глубину любой вершины не менее расстояния от начальной вершины и не более общего числа вершин, причем в худшем случае время поиска в глубину может быть максимальным, независимо от расстояния до начальной вершины.

Следствие3. Пусть (u1, ..., ui, ..., uр) – обход при поиске в ширину, a D(u1, 1), D(u1, 2), ... – ярусы графа относительно вершины u1. Тогда

Другими словами, время поиска в ширину ограничено снизу количеством вершин во всех ярусах, находящихся на расстоянии меньшем, чем расстояние от начальной вершины до текущей, и ограничено сверху количеством вершин в ярусах, начиная с яруса текущей вершины и включая все меньшие ярусы.

Следствие 4. Пусть (u1, ..., ui, ..., uр) – обход при поиске в ширину, a (x1, ..., xj, ..., xp) – обход при поиске в глубину, где ui = xj. Тогда в среднем i = 2j.

Другими словами, поиск в глубину в среднем вдвое быстрее, чем поиск в ширину.