
- •ОГЛАВЛЕНИЕ
- •ВВЕДЕНИЕ
- •ГЛАВА 1
- •1.1. Основное определение
- •1.2. Орграфы, псевдографы, мультиграфы и гиперграфы
- •1.3. Смежность
- •1.4. Изоморфизм графов
- •1.5. Элементы графов
- •1.6. Виды графов
- •1.7. Графы и отношения
- •1.8. Способы представления графов в памяти компьютера
- •ГЛАВА 2
- •2.1. Объединение графов и компоненты связности
- •2.2. Вершинная и реберная связность
- •2.3. Непересекающиеся цепи и разделяющие множества
- •2.4. Теорема Менгера
- •2.5. Теорема Холла
- •2.6. Связность в орграфах
- •2.7. Алгоритмы нахождения кратчайших путей
- •ГЛАВА 3
- •3.2. Потоки в сетях
- •БИБЛИОГРАФИЧЕСКИЙ СПИСОК
- •Приложение
В. А. Карнаухов |
Теория графов и сетей при моделировании |
|
процессов УВД. Учебное пособие. |
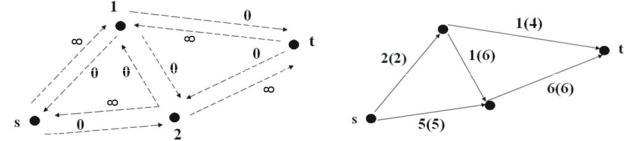
Рис. 26. Орграф приращений I(Н, 6) для сети |
Рис. 27. Сеть с полученным потоком (s, t) = 7 |
|
после второго цикла работы алгоритма |
Полученный поток является искомым максимальным допустимым потоком, т. к., если построить новый орграф приращений, то в нем не найдется пути нулевой длины из s в t (данное утверждение необходимо предлагается проверить самостоятельно). На самостоятельную проработку остается также проверка допустимости потока, полученного при решении задачи.
Существуют и более сложные, но в то же время практически более значимые варианты потоковых задач, такие как планирование максимального потока наименьшей стоимости, планирование потока в сети, где пропускная способность дуг меняется со временем и др.
3.2. Потоки в сетях
Рассмотрим некоторые примеры практических задач о потоках в сетях.
1.Существует некая сеть автомобильных дорог, по которым можно проехать из пункта A в пункт В. Дороги могут пересекаться в промежуточных пунктах. Количество автомобилей, которые могут проехать по каждому отрезку дороги за единицу времени, небезгранично: оно определяется такими факторами, как ширина проезжей части, качество дорожного покрытия, действующие ограничения скорости движения и т. д. (обычно это называют пропускной способностью дороги). Каково максимальное количество автомобилей, которые могут проехать из пункта A в пункт В за единицу времени без образования пробок на дорогах (обычно это называют автомобильным потоком)? Можно поставить и другой вопрос: какие дороги и насколько необходимо расширить или улучшить, чтобы увеличить максимальный автомобильный поток на заданную величину?
2.Пусть существует сеть трубопроводов, соединяющих пункт А (скажем, нефтепромысел) с пунктом В (скажем, нефтеперерабатывающим заводом).
© НИЛ НОТ НИО УВАУ ГА(и), 2012 г |
52 |
В. А. Карнаухов |
Теория графов и сетей при моделировании |
|
процессов УВД. Учебное пособие. |
Трубопроводы могут соединяться и разветвляться в промежуточных пунктах. Количество нефти, которое может быть перекачано по каждому отрезку трубопровода в единицу времени, также небезгранично и определяется такими факторами, как диаметр трубы, мощность нагнетающего насоса и т. д. (обычно это называют пропускной способностью или максимальным расходом трубопровода). Сколько нефти можно прокачать через такую сеть за единицу времени?
3. Пусть существует система машин для производства готовых изделий из сырья и последовательность технологических операций может быть различной (т. е. операции могут выполняться на разном оборудовании или в разной последовательности), но все допустимые варианты заранее строго определены. Максимальная производительность каждой единицы оборудования, естественно, также заранее известна и постоянна. Какова максимально возможная производительность всей системы в целом? Как нужно организовать производство для достижения максимальной производительности?
Изучение этих и подобных им многочисленных практических задач приводит к теории потоков в сетях. В данном разделе рассматривается решение только одной (но самой существенной) задачи этой теории, а именно: задачи определения максимального потока. Описание других родственных задач, например, задачи определения критического пути, можно найти в библиографическом списке.
Определение потока
Пусть G (X, V) – сеть, s и t – источник и сток сети соответственно. Дуги сети нагружены неотрицательными вещественными числами, с: V R+. Если u и x – узлы сети, то число с(и, x) называется пропускной способностью дуги (u, x).
Матрица пропускных способностей С: array [1...p, 1...p] of real является представлением сети, аналогичным матрице смежности. Нулевое значение элемента С[и, x] соответствует дуге с нулевой пропускной способностью, т. е. отсутствию дуги, а положительное значение элемента С[и, x] соответствует дуге с ненулевой пропускной способностью, т. е. дуга присутствует.
Пусть задана функция f: V R. Дивергенцией функции f в узле x называется число div(f, x), которое определяется следующим образом:
© НИЛ НОТ НИО УВАУ ГА(и), 2012 г |
53 |
В. А. Карнаухов |
|
|
|
|
|
Теория графов и сетей при моделировании |
|
|
|
|
|
|
процессов УВД. Учебное пособие. |
def |
|
|
f (u, x) |
|
|
f (x, u) . |
div( f , u) |
|
|
|
|
||
|
{x |
|
(u, x) V } |
{x |
|
( x, u) V } |
|
|
|
В физике дивергенция обычно определяется наоборот: то, что пришло, минус то, что ушло. Но в данном случае удобнее, чтобы дивергенция источника была положительна.
Функция f: V R называется потоком в сети G, если:
1) u, x V (0 f (u, x) c(u, x)) , т. е. поток через дугу не отрицателен и не превосходит ее пропускной способности;
2) u X \ {s, t} (div( f , u) 0) , т. е. дивергенция потока равна нулю во всех узлах, кроме источника и стока.
def
Число w( f ) div( f , s) называется величиной потока f. Если f(u, x) = c(u, x), то дуга (и, x) называется насыщенной.
Разрезы
Пусть Р – (s, t)-разрез, Р V. Всякий разрез определяется разбиением множества вершин X на два подмножества S и Т так, что S X, Т X, S Т = X, ST = , s S, t Т, а в Р попадают все дуги, соединяющие S и Т. Тогда Р = Р+Р–, где Р+ – дуги от S к Т, Р– – дуги от T к S. Сумма потоков через дуги разреза Р обозначается F(P). Сумма пропускных способностей дуг разреза P называется пропускной способностью разреза и обозначается С(Р):
def |
f (v), |
def |
c(v). |
F(P) |
C(P) |
||
|
v P |
|
v P |
Аналогично, F(P+) и F(P–) – суммы потоков через соответствующие части разрезов.
Теорема Форда–Фалкерсона
В данном подразделе устанавливается количественная связь между величиной максимального потока и пропускными способностями дуг сети.
Лемма1. w(f) = F(P+) – F(P–).
Доказательство. Рассмотрим сумму W div( f , x) .
x S
© НИЛ НОТ НИО УВАУ ГА(и), 2012 г |
54 |
В. А. Карнаухов |
Теория графов и сетей при моделировании |
|
процессов УВД. Учебное пособие. |
Пусть дуга (и, x) V. Если (u, x) S, то в сумму W попадают два слагаемых для этой дуги: +f(u, x) при вычислении div(f, и) и –f(u, x) при вычислении div(f, x), итого 0. Если u S, x T, то в сумму W попадает одно слагаемое +f(u, x), все такие слагаемые дают F(Р+). Если и Т, x S, то в сумму W попадает одно слагаемое – f(u, x), все такие слагаемые дают F(P–). Таким образом, W = F(Р+) – F(P–).
С другой стороны,
W : div( f , x) div( f , s) w( f ) .
x S
Лемма2. div(f, s) = –div(f, t).
Доказательство. Рассмотрим разрез P := (S, T), где S := X – t, a T := {t}. Имеем:
div(f, s) = w(f) = F(P+) – F(P–) = F(P+) = f (x, t) div( f , t) .
x
Лемма 3. w(f) F(P).
Доказательство. w(f) = F(P+) – F(P–) F(P+) F(P).
Лемма 4. max w( f ) min C(P) .
f P
Доказательство. По предыдущей лемме w(f) F(P), следовательно,
max w( f ) min F(P) . |
|
f |
P |
По определению: F(P) C(P), следовательно, min F( f ) min C(P) .
P P
Имеем: max w( f ) min C(P) .
f |
P |
Теорема (Форда–Фалкерсона). Максимальный поток в сети равен минимальной пропускной способности разреза, то есть существует поток f*, такой, что
w( f * ) max w( f ) min C(P) . |
|
f |
P |
Доказательство. Пусть f – некоторый максимальный поток. Покажем, что существует разрез P, такой, что w(f) = С(Р).
Рассмотрим граф G', полученный из сети G забыванием ориентации дуг. Построим множество вершин S следующим образом:
def |
|
|
S {u X |
|
s, u G' (ui , ui 1) s, u G' |
((ui , ui 1) V f (ui , |
ui 1) C(ui , ui 1) & (ui , ui 1) V (ui , ui 1) 0)}, |
|
© НИЛ НОТ НИО УВАУ ГА(и), 2012 г |
55 |
В. А. Карнаухов |
Теория графов и сетей при моделировании |
|
процессов УВД. Учебное пособие. |
т. е. вдоль пути s, u дуги в направлении пути не насыщены, а дуги против направления пути имеют положительный поток. Такая цепь s, u называется аугментальной. Имеем s S по построению. Следовательно, S . Положим T := X \ S. Покажем, что t Т. Пусть t S. Тогда существует аугментальная цепь s, t , обозначим ее R. Можно найти число > 0:
min (v) ,
v R
c(v) f (v) 0, если v ориентировать вдоль R,
где (v)
f (v) 0, если v ориентировать против R.
В этом случае можно увеличить величину потока на , изменив поток для всех дуг аугментальной цепи:
f (v) , если v ориентировать вдоль R, f (v)
f (v) , если v ориентировать против R.
При этом условия потока выполняются: 0 f (v) C(v), div(x) 0 .
Таким образом, поток f увеличен на величину , что противоречит максимальности потока f. Имеем t Т и Т . Следовательно, S и Т определяют разрез Р = Р+ P–. В этом разрезе все дуги v+ насыщены (f(v+) = c(v+)), а все дуги v– не нагружены (f(v–) = 0), иначе S можно было бы расширить.
Имеем: w(f) = F(P+) – F(P–) = С(Р+), таким образом, Р+ – искомый разрез.
Алгоритм нахождения максимального потока
Следующий алгоритм определяет максимальный поток в сети, заданной матрицей пропускных способностей дуг. Этот алгоритм использует идею доказательства теоремы Форда– Фалкерсона: задавшись начальным приближением потока, определяем множество вершин S, которые соединены аугментальными цепями с источником s. Если оказывается, что t S, то это означает, что поток не максимальный и его можно увеличить на величину . Для определения аугментальных цепей и одновременного подсчета величины в алгоритме использована вспомогательная структура данных:
Р: array [1...p] of record
s: enum (–, +) |
{«знак», т. е. направление дуги} |
© НИЛ НОТ НИО УВАУ ГА(и), 2012 г |
56 |
В. А. Карнаухов |
Теория графов и сетей при моделировании |
|
процессов УВД. Учебное пособие. |
n: 1..р |
{предшествующая вершина в аугментальной цепи} |
|
: real |
{величина возможного увеличения потока} |
|
end record |
|
|
N: array [1...p] of 0...1 |
{отметка узла} |
|
S: array [1...p] of 0...1 |
{признак принадлежности вершины множеству S} |
|
Вход: сеть G (X, V) с источником s и стоком t, заданная матрица пропускных способностей С: array [1...p, 1...p] of real.
Выход: матрица максимального потока F: array [1...p, 1...p] of real.
for u, x X do
F[u, x] := 0 end for
M:
for x X do
S[x] := 0; N[x] := 0; P[x] := (+, nil, 0) end for
S[s] := 1; P[s] := (+, nil, ) {так как s S} repeat
а := 0
for x X do
if S[x] = 1 & N[x] = 0 then for u Г(x) do
if S[u] = 0 & F[x, u] < C[x, u] then
S[u] := 1; P[u] := (+, x, min (P[x]. , C[x, u] – F[x, u])); а := 1 end if
end for
for u Г-1(x) do
if S[u] = 0 & F[u, x] > 0 then
S[u] := 1; P[u] := (–, u, min (P[x]. F[u, x])); a := 1 end if
end for
N[x] := 1 end if
end for
if S[t] then x := t
© НИЛ НОТ НИО УВАУ ГА(и), 2012 г |
57 |
В. А. Карнаухов |
Теория графов и сетей при моделировании |
|
процессов УВД. Учебное пособие. |
:= P[t]. {величина изменения потока} while х ≠ s do
if P[x].s = + then
F[P[x].n, x] := F[P[x].n, x] + else
F[x, P[x].n] := F[x, P[x].n] – end if
x := P[x].n end while
goto M end if
until a = 0
Обоснование. В качестве первого приближения берется нулевой поток, который по определению является допустимым. В основном цикле, помеченном меткой М, делается попытка увеличить поток. Для этого в цикле repeat расширяется, насколько это возможно, множество S-узлов, достижимых из источника s по аугментальным цепям. При этом если во множество S попадает сток t, то поток вдоль найденной аугментальной цепи (s, t) немедленно увеличивается на величину , и начинается новая итерация с целью увеличить поток. Процесс расширения множества S в цикле repeat заканчивается, потому что множество узлов конечно, а отмеченные в массиве N узлы повторно не рассматриваются. Если процесс расширения множества S заканчивается и при этом сток t не попадает во множество S, то по теореме Форда– Фалкерсона найденный поток F является максимальным и работа алгоритма завершается.
© НИЛ НОТ НИО УВАУ ГА(и), 2012 г |
58 |
