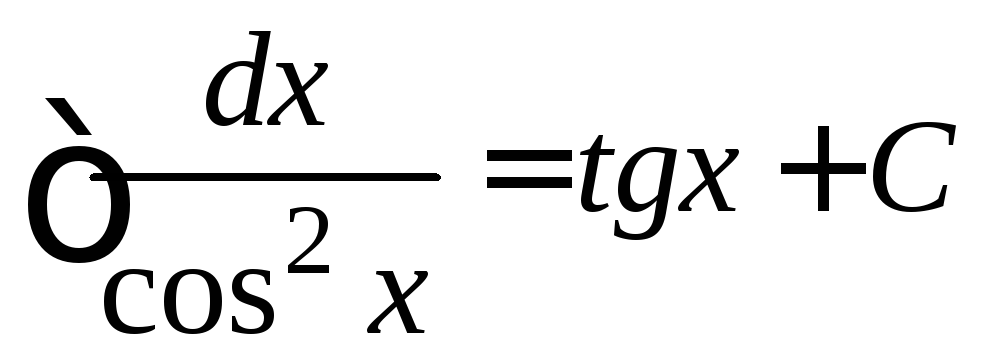- •Федеральное агентство по образованию
- •М. М. Афанасьева, о.С. Громова, в. А. Павский
- •В 3-х частях
- •Часть 2
- •Isb n 5-89289-216-6
- •Правила выполнения и оформления контрольных работ
- •Тема 1. Функции нескольких переменных
- •1.1 Общие сведения
- •1.2 Производные и дифференциалы
- •1.3 Экстремумы функции нескольких переменных
- •1.4 Скалярное поле. Производная по направлению. Градиент
- •Тема 2. Комплексные числа
- •Комплексная плоскость
- •Действия над комплексными числами
- •Тема 3. ОпределенныЙ и неопределенный интегралы
- •3.1 Основные понятия и теоремы Задача, приводящая к понятию определенного интеграла
- •Определенный интеграл
- •I этап.
- •Связь интегрирования с дифференцированием
- •Неопределенный интеграл
- •Формула ньютона-лейбница
- •, Где .
- •Свойства интегралов
- •Метод интегрирования по частям
- •3.3 Основные классы интегрируемых функций
- •Интегрирование рациональных функций
- •1 Случай.
- •2 Случай.
- •3 Случай.
- •Интегрирование иррациональных функций
- •Интегрирование тригонометрических функций
- •3.4 Несобственные интегралы
- •Несобственный интеграл с бесконечными пределами
- •Несобственный интеграл от неограниченной функции
- •3.5 Приложения интегрального исчисления к геометрии Применение определенных интегралов к вычислению площадей
- •Вычисление длины дуги плоской кривой
- •Вычисление объёмов
- •Тема 4. Дифференциальные уравнения
- •4.1 Основные понятия
- •4.2 Дифференциальные уравнения 1-го порядка
- •Дифференциальные уравнения с разделёнными переменными
- •Дифференциальные уравнения с разделяющимися переменными
- •Однородные дифференциальные уравнения 1-го порядка
- •Линейные дифференциальные уравнения 1-го порядка
- •4.3 Дифференциальные уравнения второго порядка
- •Дифференциальные уравнения 2-го порядка, допускающие понижение порядка
- •Линейные дифференциальные уравнения второго порядка
- •Линейные уравнения 2-го порядка с постоянными коэффициентами
- •4.4 Задачи на составление дифференциальных уравнений
- •Тема 5. Ряды
- •5.1 Числовые ряды
- •5.2 Числовые ряды с положительными членами
- •Интегральный признак Коши
- •Первый признак сравнения
- •Второй признак сравнения
- •Признак Даламбера
- •5.3 Знакопеременные ряды
- •Знакопеременные ряды. Абсолютная и условная сходимость
- •Достаточный признак сходимости
- •5.4 Степенные ряды
- •Теорема Абеля
- •Свойства степенных рядов
- •5.5 Разложение функции в степенной ряд. Ряд Тейлора
- •Разложение по степеням X некоторых элементарных функций
- •5.6 Применение степенных рядов Интегрирование функций
- •Интегрирование дифференциальных уравнений
- •Контрольные задания
- •9. . 10..
Связь интегрирования с дифференцированием
Рассмотрим определенный интеграл, у которого нижний предел остается постоянным, а верхний изменяется.
Придавая верхнему пределу различные значения, будем получать различные значения интеграла; следовательно, при этих условиях интеграл является функцией своего верхнего предела
 ,
,
здесь
![]() -
переменная интегрирования, изменяющаяся
в промежутке
-
переменная интегрирования, изменяющаяся
в промежутке
![]() .
.
ТЕОРЕМА
1. Производная
от интеграла по его верхнему пределу
равна подынтегральной функции  .
.
ДОКАЗАТЕЛЬСТВО
Рассмотрим
непрерывную, принимающую неотрицательные
значения в промежутке
![]() функцию
функцию![]() .
Зафиксируем точку
.
Зафиксируем точку![]() и обозначим через
и обозначим через![]() площадь криволинейной трапеции с
основанием
площадь криволинейной трапеции с
основанием![]() ,
,![]() (рис. 9), тогда
(рис. 9), тогда

 .
.
Если
переменная
![]() получит приращение
получит приращение![]() ,
то
,
то![]() изменится на
изменится на![]() (см.
рис. 9). Геометрически ясно, что
(см.
рис. 9). Геометрически ясно, что
![]() ,
,
где
![]() и
и![]() -
соответственно наименьшее и наибольшее
значения функции
-
соответственно наименьшее и наибольшее
значения функции![]() в промежутке
в промежутке
![]() .
Ведь
.
Ведь![]() - площадь прямоугольника, целиком
лежащего внутри фигуры, площадь которой
обозначена
- площадь прямоугольника, целиком
лежащего внутри фигуры, площадь которой
обозначена![]() ,
а
,
а![]() - площадь прямоугольника, содержащего
эту фигуру. Разделим все части неравенства
на приращение
- площадь прямоугольника, содержащего
эту фигуру. Разделим все части неравенства
на приращение![]() ,
тогда
,
тогда .
.
Так
как
![]() непрерывная функция на отрезке
непрерывная функция на отрезке![]() ,
то она принимает в этом интервале хотя
бы один раз любое значение, заключенное
между ее наименьшим и наибольшим
значениями, в том числе и значение
,
то она принимает в этом интервале хотя
бы один раз любое значение, заключенное
между ее наименьшим и наибольшим
значениями, в том числе и значение![]() .
Обозначим через
.
Обозначим через![]() точку, в
которой
точку, в
которой
 ,
,
![]() .
.
Рассмотрим
предел этого выражения при условии, что
![]() .
Тогда точка
.
Тогда точка![]() ,
а значение
,
а значение![]() к значению функции
к значению функции![]() .
По свойствам пределов будем иметь:
.
По свойствам пределов будем иметь:
 ,
,  .
.
ЗАМЕЧАНИЕ: Эта теорема показывает, что интегрирование и дифференцирование - обратные операции.
Неопределенный интеграл
ОПРЕДЕЛЕНИЕ. Функцию F(x), производная которой равна подынтегральной функции, называют первообразной.
Как нахождение производной было одной из основных задач дифференциального исчисления, так нахождение первообразной является одной из основных задач интегрального исчисления.
Например,
рассмотрим функцию
![]() .
Мы знаем, что
.
Мы знаем, что![]() .
Функция
.
Функция![]() первообразная для функции
первообразная для функции![]() .
.
Если
найти производные от функций
![]() ,
,![]() ,
,![]() ,
где
,
где![]() -
произвольная постоянная величина, то
все они равны
-
произвольная постоянная величина, то
все они равны![]() .
Следовательно, любая из функций
.
Следовательно, любая из функций![]() является первообразной для функции
является первообразной для функции![]() .
.
ТЕОРЕМА 2. Всякая непрерывная функция имеет бесчисленное множество первообразных, причем любые две из них отличаются друг от друга только постоянным слагаемым.
ДОКАЗАТЕЛЬСТВО.
Предположим,
что функция
![]() имеет первообразную функцию
имеет первообразную функцию![]() .
Тогда функция
.
Тогда функция![]() при всякой постоянной
при всякой постоянной![]() будет также первообразной, так как
будет также первообразной, так как![]() .
Итак, функция
.
Итак, функция![]() имеет бесчисленное множество первообразных.
имеет бесчисленное множество первообразных.
Пусть
функции
![]() и
и![]() - первообразные для функции
- первообразные для функции![]() ,
т.е.
,
т.е.![]() и
и![]() .
Тогда
.
Тогда![]() .
Но
.
Но![]() .
Следовательно,
.
Следовательно,![]() .
.
ОПРЕДЕЛЕНИЕ. Совокупность всех первообразных для подынтегральной функции называется неопределенным интегралом.
Неопределенный
интеграл обозначается также как и
определенный, только без указания
границ, т.е. если ![]() ,
то
,
то
![]() .
.
И з
этой формулы следуют равенства:
з
этой формулы следуют равенства:
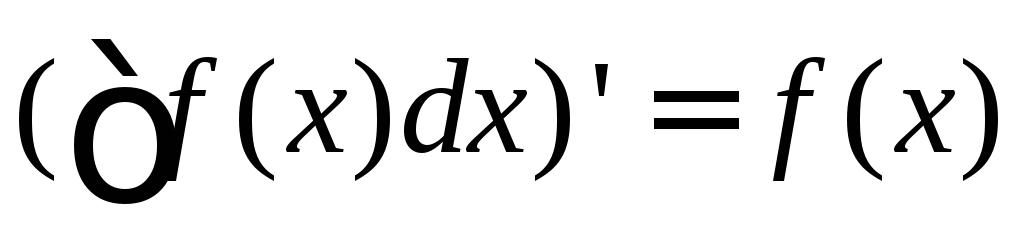 ,
,
 ,
, .
.
График
первообразной для функции
![]() называетсяинтегральной
кривой
функции
называетсяинтегральной
кривой
функции
![]() .
.
Из
определения неопределенного интеграла
как совокупности первообразных
![]() следует, что семейство всех интегральных
кривых может быть получено параллельным
переносом линии
следует, что семейство всех интегральных
кривых может быть получено параллельным
переносом линии![]() на величину
на величину![]() в направлении оси ординат (рис. 10).
в направлении оси ординат (рис. 10).
В таблице 1 приведены производные и первообразные для основных элементарных функций.
ТАБЛИЦА 1
|
Таблица производных |
Таблица интегралов |
|
1. |
1. |
|
2.
|
2.
|
|
3.
|
3.
|
|
4.
|
4. |
|
5.
|
5.
|
|
6.
|
6.
|
|
7.
|
7.
|
|
8.
|
8.
|
|
9.
|
9.
|
|
10.
|
10.
|
|
11.
|
Замечание: справедливость формул можно проверить дифференцированием. |
|
12.
|
Связь между определенным и неопределенным интегралом показывает формула НЬЮТОНА-ЛЕЙБНИЦА.