4.4 Задачи на составление дифференциальных уравнений

ПРИМЕР.

Пусть население некоторого территориального образования составляет на данный момент времени человек. Предполагая, что скорость прироста населения пропорциональна его начальному количеству, найдем закон, по которому можно определить количество населения в любой другой год.

РЕШЕНИЕ.

Учитывая, что скорость изменения величины есть производная, и, обозначив коэффициент пропорциональности черезk , получим дифференциальное уравнение: . Преобразуем его к виду:.

Проинтегрировав, , получим общий интегралили.

Пусть в рассматриваемый (начальный) момент времени t₀=0 население составило 200 тыс. человек. При благоприятных условиях ежегодный прирост составил 2%. Определить количество населения через 10 лет.

Итак: t₀ = 0, x₀ = 200 подставляя в функцию , находим, что=200, то есть.

Т.к. ежегодный прирост составил 2%, то

при t₁ = 1.

Используя полученные значения x₁ и t₁ , найдем k из уравнения :,.

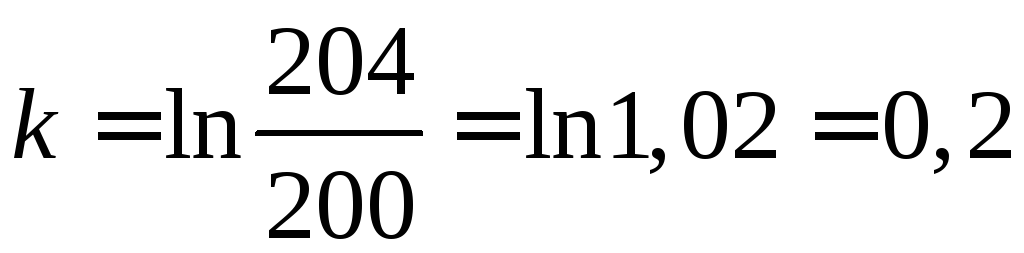Поэтому уравнение примет вид:

.

Через 10 лет населения составит:

,

ПРИМЕР. При брожении скорость прироста действующего фермента пропорциональна его имеющейся массе. Через 2 часа после начала брожения масса фермента составила 2 г, а через 3 часа – 3 г. Какова была первоначальная масса фермента?

РЕШЕНИЕ

Обозначим через - время,- массу фермента послечасов после начала брожения. Тогда скорость прироста действующего фермента равна.

По условию скорость роста фермента пропорциональна его массе, поэтому где- коэффициент пропорциональности. Таким образом, получили дифференциальное уравнение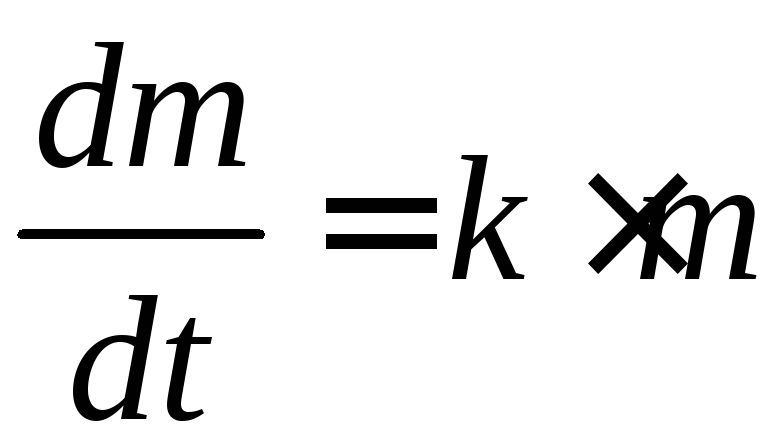. Найдем общее решение этого уравнения с разделяющимися переменными

Полученное равенство выражает зависимость массы фермента от времени брожения.

Чтобы найти содержащиеся в этом равенстве постоянные, используем заданные условия

Подставив эти условия в, получим систему, из которой найдем и:

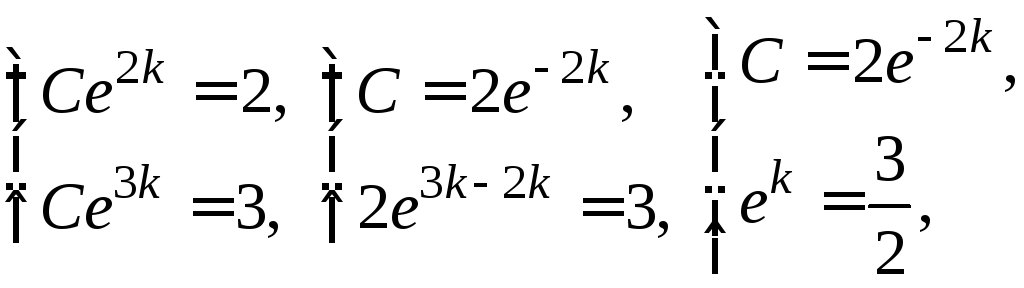
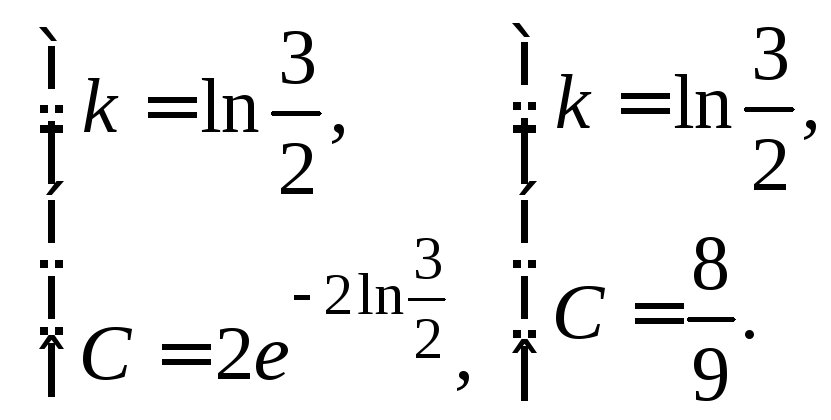
Теперь равенство примет вид . Равенство дает возможность вычислить массу фермента в любой момент времени.

Тема 5. Ряды

5.1 Числовые ряды

ОПРЕДЕЛЕНИЕ. Если числа образуют бесконечную числовую последовательность, то выражение вида

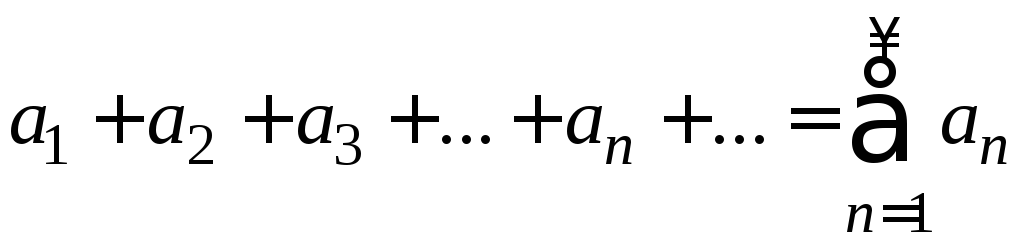
называют числовым рядом. Числа называют членами ряда, а - общим членом ряда.

ОПРЕДЕЛЕНИЕ. Последовательность ,,,,,называют последовательностью частичных сумм ряда.

ОПРЕДЕЛЕНИЕ. Конечный или бесконечный предел частичной суммыряда при условии, что: называют его суммой и пишут .

Если ряд имеет конечную сумму, его называют сходящимся, в противном случае (т.е. если сумма равна , либо суммы вовсе нет) – расходящимся.

Например.

1) Рассмотрим числовой ряд .

Последовательность частичных сумм для этого ряда имеет вид: ,,,,,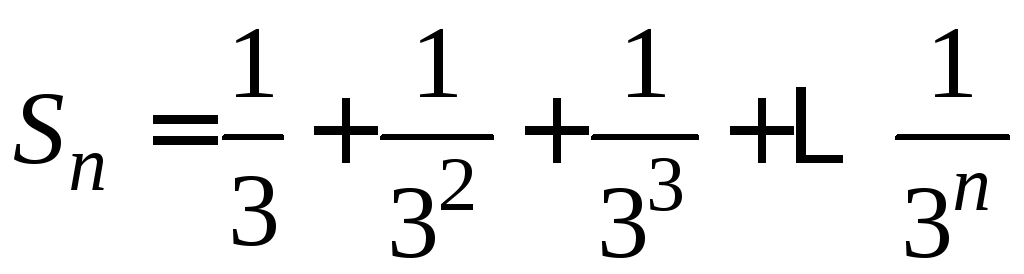. Так как сумма первых- членов геометрической прогрессии может быть найдена по формуле, (здесь- первый член прогрессии,- знаменатель прогрессии), то сумма ряда будет равна

.

Таким образом, ряд сходится и его сумма равна .

2) Для ряда частичные суммы равны,,,,,и поэтому сумма ряда. Значит, ряд расходится.

3) Рассмотрим ряд, составленный из членов геометрической прогрессии

Его частичная сумма будет равна (если ). Если знаменатель прогрессиито, т.е. ряд сходится. При условии, чторяд расходится: если, то его суммой будет бесконечность (определенного знака), в прочих случаях суммы вовсе нет.

Рассмотрим сходящийся числовой ряд. Разность между суммой ряда и его частичной суммойназывают-м остатком ряда

.

Остаток ряда представляет собой ту погрешность, которая получается, если в качестве приближенного значения суммы рядавзять сумму первыхчленовэтого ряда.

Так как предел последовательности, то,.

Поэтому, взяв достаточно большое число членов сходящегося ряда, можно вычислить сумму ряда с любой степенью точности.

Сходящиеся числовые ряды обладают некоторыми свойствами, которые позволяют действовать с ними, как с конечными суммами.

1. Если члены сходящегося ряда умножить на один и тот же множитель , то его сходимость не нарушится, а сумма ряда умножится на число.

2. Два сходящихся ряда иможно почленно складывать (или

вычитать), вновь полученный ряд также сходится.

3. Если ряд сходится, то сходится и ряд, полученный из данного добавлением или отбрасыванием конечного числа членов.

4. Необходимый признак сходимости ряда

Если ряд сходится, то его общий членпри неограниченном

увеличение номера n стремится к нулю, т.е. .

ДОКАЗАТЕЛЬСТВО

Если числовой ряд сходится, то как , так иприимеют конечный предел. Следовательно, поскольку, имеем

.

Таким образом, ряд может сходиться только при условии, что . Если жеили не существует, то ряд расходится. Это условие являетсядостаточным признаком расходимости ряда.

ПРИМЕР. Рассмотрим числовой ряд .

Найдем предел общего члена , т. е. ряд расходится.