
- •Федеральное агентство по образованию
- •М. М. Афанасьева, о.С. Громова, в. А. Павский
- •В 3-х частях
- •Часть 2
- •Isb n 5-89289-216-6
- •Правила выполнения и оформления контрольных работ
- •Тема 1. Функции нескольких переменных
- •1.1 Общие сведения
- •1.2 Производные и дифференциалы
- •1.3 Экстремумы функции нескольких переменных
- •1.4 Скалярное поле. Производная по направлению. Градиент
- •Тема 2. Комплексные числа
- •Комплексная плоскость
- •Действия над комплексными числами
- •Тема 3. ОпределенныЙ и неопределенный интегралы
- •3.1 Основные понятия и теоремы Задача, приводящая к понятию определенного интеграла
- •Определенный интеграл
- •I этап.
- •Связь интегрирования с дифференцированием
- •Неопределенный интеграл
- •Формула ньютона-лейбница
- •, Где .
- •Свойства интегралов
- •Метод интегрирования по частям
- •3.3 Основные классы интегрируемых функций
- •Интегрирование рациональных функций
- •1 Случай.
- •2 Случай.
- •3 Случай.
- •Интегрирование иррациональных функций
- •Интегрирование тригонометрических функций
- •3.4 Несобственные интегралы
- •Несобственный интеграл с бесконечными пределами
- •Несобственный интеграл от неограниченной функции
- •3.5 Приложения интегрального исчисления к геометрии Применение определенных интегралов к вычислению площадей
- •Вычисление длины дуги плоской кривой
- •Вычисление объёмов
- •Тема 4. Дифференциальные уравнения
- •4.1 Основные понятия
- •4.2 Дифференциальные уравнения 1-го порядка
- •Дифференциальные уравнения с разделёнными переменными
- •Дифференциальные уравнения с разделяющимися переменными
- •Однородные дифференциальные уравнения 1-го порядка
- •Линейные дифференциальные уравнения 1-го порядка
- •4.3 Дифференциальные уравнения второго порядка
- •Дифференциальные уравнения 2-го порядка, допускающие понижение порядка
- •Линейные дифференциальные уравнения второго порядка
- •Линейные уравнения 2-го порядка с постоянными коэффициентами
- •4.4 Задачи на составление дифференциальных уравнений
- •Тема 5. Ряды
- •5.1 Числовые ряды
- •5.2 Числовые ряды с положительными членами
- •Интегральный признак Коши
- •Первый признак сравнения
- •Второй признак сравнения
- •Признак Даламбера
- •5.3 Знакопеременные ряды
- •Знакопеременные ряды. Абсолютная и условная сходимость
- •Достаточный признак сходимости
- •5.4 Степенные ряды
- •Теорема Абеля
- •Свойства степенных рядов
- •5.5 Разложение функции в степенной ряд. Ряд Тейлора
- •Разложение по степеням X некоторых элементарных функций
- •5.6 Применение степенных рядов Интегрирование функций
- •Интегрирование дифференциальных уравнений
- •Контрольные задания
- •9. . 10..
Тема 2. Комплексные числа
Если ограничиваться только вещественными числами, то, действие извлечения корня не всегда выполнимо: корень четной степени из отрицательного числа не имеет ответа в области вещественных чисел. Это обстоятельство приводит к необходимости расширения понятия о числе и введению новых чисел с более общими свойствами.
Комплексная плоскость
ОПРЕДЕЛЕНИЕ. Комплексным
числом называют выражение вида
![]() ,
где
,
где![]() и
и![]() - действительные числа, а
- действительные числа, а![]() -
мнимая единица, удовлетворяющая равенству
-
мнимая единица, удовлетворяющая равенству![]() .
.
Такую
форму записи комплексного числа называют
алгебраической
формой,
причем
![]() -вещественной
частью,
а
-вещественной
частью,
а
![]() -мнимой
частью,
что записывается так:
-мнимой
частью,
что записывается так:
![]() ,
,![]() .
.

 Комплексные
числа можно изобразить на плоскости.
Для этого выбирают систему декартовых
координат
Комплексные
числа можно изобразить на плоскости.
Для этого выбирают систему декартовых
координат
![]() ,
,![]() ,
после чего любое комплексное число
,
после чего любое комплексное число![]() отождествляется с радиус-вектором точки
отождествляется с радиус-вектором точки![]() (рис. 5). Такую плоскость называюткомплексной
плоскостью.
(рис. 5). Такую плоскость называюткомплексной
плоскостью.
Действительные
(вещественные) числа являются частным
случаем комплексных чисел, если в формуле
![]() положить
положить![]() .
Они изображаются точками на вещественной
оси, т. е. оси
.
Они изображаются точками на вещественной
оси, т. е. оси![]() .
Если у комплексного числа отсутствует
действительная часть
.
Если у комплексного числа отсутствует
действительная часть![]() ,
то его называют чисто мнимым и изображают
на мнимой оси, т.е. оси
,
то его называют чисто мнимым и изображают
на мнимой оси, т.е. оси![]() .
.
На
рис.6 показаны комплексные числа
![]() ,
,![]() и
и![]() .
.
На
комплексной плоскости часто рассматривают
также полярные координаты
![]() и
и![]() точки
точки![]() .
Их называютмодулем
и аргументом
комплексного
числа
.
Их называютмодулем
и аргументом
комплексного
числа
![]() и обозначают
и обозначают![]() ,
,![]() (рис. 5). Связь между модулем и аргументом
комплексного числа
(рис. 5). Связь между модулем и аргументом
комплексного числа![]() и его действительной и мнимой частями
устанавливается известными формулами:
и его действительной и мнимой частями
устанавливается известными формулами:
![]() ,
, ![]() ,
, ![]() ,
,
 ,
,  ,
, .
.
Заменяя
![]() и
и![]() в алгебраической форме комплексного
числа
в алгебраической форме комплексного
числа![]() ,
их выражениями через
,
их выражениями через![]() и
и![]() ,
получим так называемуютригонометрическую
форму
комплексного
числа:
,
получим так называемуютригонометрическую
форму
комплексного
числа:
![]() .
.
Модуль
любого комплексного числа имеет вполне
определенное значение, тогда как аргумент
определен с точностью до целого числа
полных оборотов. Поэтому значение
полярного угла
![]() ,
которое удовлетворяет неравенству
,
которое удовлетворяет неравенству![]() ,
называетсяглавным
значением
аргумента
,
называетсяглавным
значением
аргумента
![]() ,
а функция
,
а функция![]() ,
где
,
где![]() –общим
значением
аргумента.
–общим
значением
аргумента.
ПРИМЕР.
Найти корни
уравнения ![]() .
.
Решение
Для
решения квадратного уравнения с
вещественными коэффициентами
![]() воспользуемся известной формулой
воспользуемся известной формулой

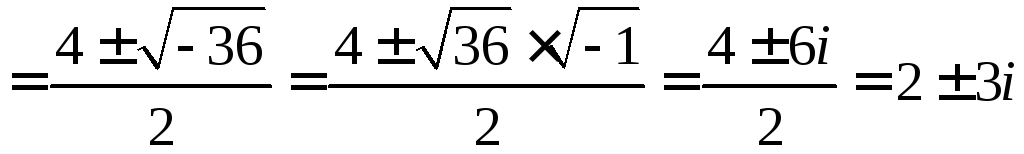 .
.
Уравнение
имеет два комплексных корня
![]() и
и![]() .
.
ПРИМЕР. Записать в тригонометрической форме комплексные числа:
a)![]() ,
б)
,
б)![]() ,
в)
,
в)![]() .
.
Решение
а)
Найдем модуль и аргумент числа
![]() .
Так как
действительная часть комплексного
числа
.
Так как
действительная часть комплексного
числа
![]() ,
а мнимая часть
,
а мнимая часть![]() ,
то
,
то
![]() ,
, .
.
Для
определения угла
![]() следует помнить, что тангенс угла
принимает положительные значения в
первой и третьей четвертях. Для определения
четверти можно изобразить точку
следует помнить, что тангенс угла
принимает положительные значения в
первой и третьей четвертях. Для определения
четверти можно изобразить точку![]() ,
соответствующую числу
,
соответствующую числу![]() на комплексной плоскости, и поскольку
она лежит в третьей четверти, то
на комплексной плоскости, и поскольку
она лежит в третьей четверти, то![]() .
Отсюда можно записать комплексное число
в тригонометрической форме
.
Отсюда можно записать комплексное число
в тригонометрической форме
![]()
![]() .
.
б)
Если ![]() ,
то
,
то![]() ,
а
,
а![]() .
.
Отсюда:
![]()
в)
Если ![]() ,
то
,
то![]() ,
,![]() .
.
Отсюда:
![]() .
.
Действия над комплексными числами
Определим на множестве комплексных чисел отношение равенства двух чисел, а также операции сложения, вычитания, умножения и деления.
Два
комплексных числа равны тогда и только
тогда, когда равны их
действительные
и мнимые части: если
![]() ,
,
![]() ,
то равенство
,
то равенство![]() равносильно двум вещественным
равносильно двум вещественным![]() и
и![]() .
.
Операции сложения и вычитания комплексных чисел удобно выполнять в алгебраической форме.
При сложении комплексных чисел складываются их вещественные части, а также их мнимые части.
Если
обозначить ![]() и
и ![]() ,
то
,
то
![]() .
.
При вычитании комплексных чисел вычитаются их вещественные части, а также их мнимые части:
![]() .
.
Умножение и деление комплексных чисел можно выполнить как в алгебраической, так и в тригонометрической форме.
Если
воспользоваться тригонометрической
формой
![]() ,
,![]() ,
то
,
то
![]() .
.
При умножении комплексных чисел их модули перемножаются, а аргументы складываются.
В
алгебраической форме ![]() .
.
Таким
образом,
комплексные
числа можно перемножать как буквенные
многочлены, считая
![]() .
.
В
частном случае, когда ![]() и
и![]() (
(![]() и
и![]() называютсопряженными
числами),
получим:
называютсопряженными
числами),
получим:
![]() .
.
Это свойство сопряженных комплексных чисел используется при делении комплексных чисел.
Модуль частного комплексных чисел равен частному модулей делимого и делителя, и аргумент частного равен разности аргументов делимого и делителя:
 ,
,
![]() .
.
Если делимое и делитель записаны в алгебраической форме, то
 ,
,
![]() .
.
Для операций сложения и умножения комплексных чисел выполняются переместительный, сочетательный и распределительный законы, а потому для выражений, содержащих комплексные числа, справедливы все те преобразования,
ПРИМЕР. Найти сумму, разность, произведение и частное комплексных чисел:
![]() и
и
![]() .
.
РЕШЕНИЕ![]()
![]() ,
,![]() ,
,
![]()
![]() .
.
Для того чтобы найти частное, умножим числитель и знаменатель дроби на выражение сопряженное знаменателю и выполним действия с многочленами:
 .
.
ПРИМЕР. Найти
произведение и частное чисел
![]() и
и![]() в тригонометрической форме.
в тригонометрической форме.
РЕШЕНИЕ
Найдем
модули и аргументы чисел
![]() и
и![]() ,
чтобы записать их в тригонометрической
форме:
,
чтобы записать их в тригонометрической
форме:
 ,
,  ,
,
![]()
 ,
, .
.
Тогда

 .
.
Теперь получим
 ,
,
 .
.
Возведение в степень комплексного числа и извлечение корня из комплексного числа производятся по формулам Муавра:
![]() ,
,
 ,
,
![]() .
.
ПРИМЕР. Вычислить
![]() .
.
РЕШЕНИЕ

ПРИМЕР.
Решить уравнение
![]() ,
если
,
если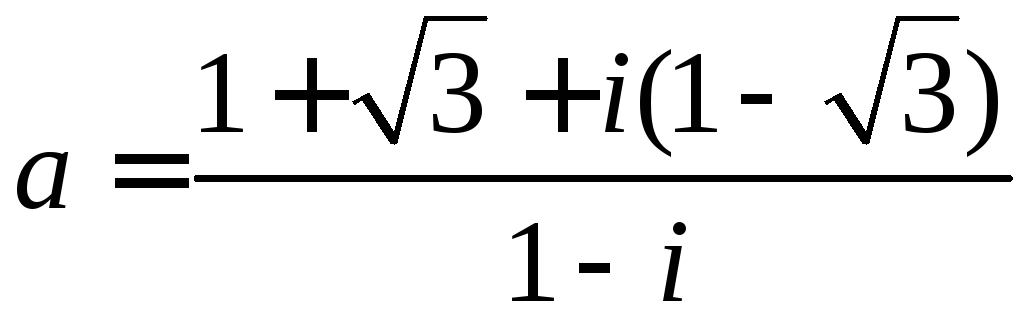 .
.
РЕШЕНИЕ
Запишем
уравнение в виде
![]() .
Выполнив деление, представим число
.
Выполнив деление, представим число![]() в алгебраической форме:
в алгебраической форме:

 .
.
Теперь
выразим число
![]() в тригонометрической форме, получим:
в тригонометрической форме, получим:
 .
.
Применим формулу Муавра:
 .
.![]() .
.
Итак, получаем 4 корня:
при
![]()
 ;
;
при
![]()
 ;
;
при
![]()
 ;
;
при
![]()
 .
.
