Тема 3. ОпределенныЙ и неопределенный интегралы

3.1 Основные понятия и теоремы Задача, приводящая к понятию определенного интеграла

Пусть задана положительная непрерывная функция . Рассмотрим эту функцию, еслиизменяется на промежутке. Восстановим перпендикуляры из точекидо пересечения с кривой. Получим фигуру, ограниченную осью, графиком непрерывной функциии двумя прямымии(рис.7). Область такого вида называюткриволинейной трапецией. Вычислим площадь этой фигуры.

Для этого разобьем промежуток наn частей произвольным образом

точками . Проведем в точках деления промежуткапрямые, параллельные оси ординат, и получимчастичных трапеций. Возьмем в каждом из частичных интервалов по произвольной точке и обозначим их через, так что

.

В точках проведем прямые, параллельные оси, до пересечения с линией; отрезки этих прямых соответственно равны,,,.

На частичных интервалах построим прямоугольников с высотойи основанием,. Площадь каждого такого прямоугольника равна.

Если просуммировать площади прямоугольников, то получим площадь ступенчатой фигуры , которая приближенно равна площади криволинейной трапеции, т.е..

Если увеличивать число прямоугольников при условии, что наибольшая длина частичного интерваластремиться к нулю, то площадь- ступенчатой фигуры будет давать более близкое значение к площади криволинейной трапеции, т.е.→, еслии.

Таким образом,

.

Итак, просуммировав площадичастичек фигуры, мы получили площадь целой фигуры, и пришли к понятию интеграла (integer – целый (лат.)). Весь изложенный ниже материал может быть представлен в виде структурно-логической схемы, которая позволит установить последовательность в изучении вопросов и связь между ними (таблица №1).

Определенный интеграл

Рассмотрим непрерывную на промежутке функцию.Разобьем отрезокнаn частей и составим интегральную сумму:

,

где по-прежнему ,.

Найдем предел интегральной суммы, если , а

.

ОПРЕДЕЛЕНИЕ. Определенным интегралом функции в промежутке отдоназывается конечный предел, к которому стремится последовательность интегральных сумм, если число разбиенийстремится к бесконечности, а длина наибольшего частичного интервала стремится к нулю, и обозначается символом.

В случае существования такого предела функция называется интегрируемой в промежутке .

Знак интеграла- стилизованная букваS (сумма), и– граничные точки области интегрирования – называют соответственнонижним и верхним пределами интегрирования, – подынтегральная функция,– подынтегральное выражение. При постоянных пределах интегрирования определенный интеграл представляет собой постоянное число.

Применяя определение интеграла к задаче о вычислении площади криволинейной трапеции, можно записать, что

, если .

ПРИМЕР. Вычислить площадь фигуры, ограниченной линиями (рис.8).

РЕШЕНИЕ

I этап.

1. Разобьем промежуток интегрирования на 5 равных частей.

2. Для простоты выберем точки в левом конце отрезков:

= 0,0; =0,2;=0,4;=0,6;=0,8.

3. Значения функции в точке будут равны.

4. Построим интегральную сумму

_.

Получим, что .

II этап. Разобьем интервал интегрирования на 10 частей и аналогично, выбрав точки ,, получим, что.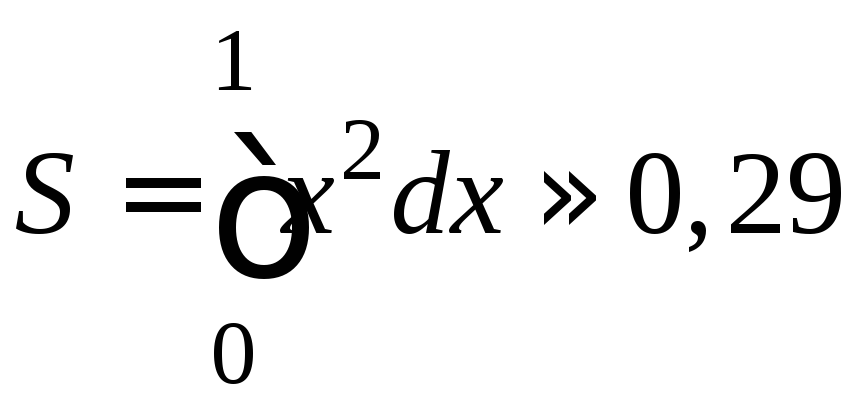

III этап. Если разобьем интервал на 100 частей, то .

В дальнейшем покажем, что точное значение площади равно 1/3. В данном примере уже после третьего разбиения видно, что S→ 1/3, но решение задачи было трудоемким. Поэтому необходимо использовать более простые приемы.