Свойства степенных рядов

Для степенных рядов справедливы следующие утверждения:

1). Сумма степенного ряда есть функция, непрерывная в интервале сходимости ряда.

2). Степенной ряд в интервале его сходимости можно почленно дифференцировать неограниченное число раз, причем получающиеся при этом степенные ряды имеют тот же радиус сходимости, что и исходный ряд, а суммы их соответственно равны , где- сумма ряда.

3). Степенной ряд можно неограниченное число раз почленно интегрировать в пределах от 0 до, если, причем получающиеся при этом степенные ряды имеют тот же радиус сходимости, что и исходный ряд.

5.5 Разложение функции в степенной ряд. Ряд Тейлора

Пусть функция, дифференцируемая бесконечное число раз в окрестности точки. Предположим, что её можно представить в виде суммы степенного ряда, сходящегося в некотором интервале, содержащем точку. Т.е.

Найдем числовые коэффициенты ,,, …,,… этого ряда. Подставим в равенство (1) значение

Отсюда .

Теперь продифференцируем равенство (1):

Подставим в равенство (2)

Отсюда .

Продифференцируем равенство (2):

(3)

Подставим в равенство (3)

Отсюда

Если продолжать дифференцирование и в получающиеся равенства подставлять , то можно последовательно найти все коэффициенты ряда (1), т.е.

Подставим найденные коэффициенты в равенство (1), тогда:

(5)

ОПРЕДЕЛЕНИЕ. Степенной ряд вида (5) называют рядом Тейлора для функции .

Чаще всего приходится иметь дело со случаем, когда и функция разлагается в ряд непосредственно по степеням

, (6)

этот ряд называют рядом Маклорена.

Составить ряд Тейлора можно для любой функции, дифференцируемой бесконечное число раз. Однако, остается открытым вопрос: будет ли полученный ряд сходиться и, если сходится, то будет ли в области сходимости его сумма равна данной функции . Обозначимчастичную сумму ряда Тейлора:

.

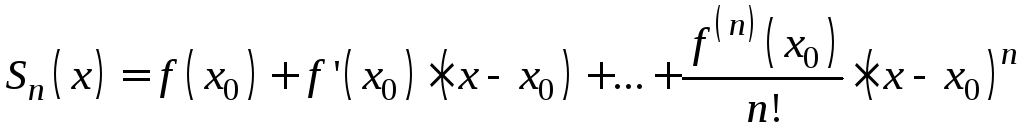Тогда

Здесь - остаток илиостаточный член ряда Тейлора.

Примем без доказательства следующее утверждение:

Ряд Тейлора представляет данную функцию только тогда, когда.

Если , то ряд Тейлора не представляет данной функции, хотя может и сходиться (к другой функции).

Если ряд Тейлора для функции сходится к этой функции, то величина остаточного членадает ошибку, которую мы делаем, заменяячастичной суммой ряда Тейлора.

Для оценки остаточного члена ряда Тейлора его можно записать в форме Лагранжа:

где

Если в некотором интервале, содержащем точку , при любомn выполняется неравенство , где постоянная, тои функцияпредставима в виде суммы ряда Тейлора.

Ниже представлены разложения в ряд Тейлора основных элементарных функций.

Используя разложения 1) – 7) таблицы 2 можно достаточно просто получить разложение элементарной функции в ряд.

ПРИМЕР. Разложить в ряд по степеням x функцию

РЕШЕНИЕ

Воспользуемся разложением (2):

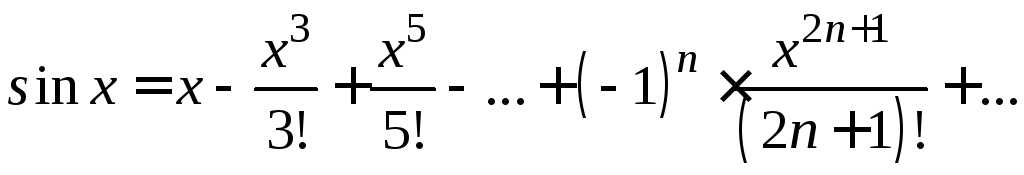
Заменим в этом разложении на :или

ПРИМЕР. Разложить в ряд по степеням функцию .

РЕШЕНИЕ

Воспользуемся разложением (1) табл.2 :

Заменим в разложении на:.

Теперь умножим все члены ряда на и получим .

_{Легко найти, что областью сходимости полученного ряда является вся числовая ось.}

ПРИМЕР. Разложить в ряд по степеням функцию.

РЕШЕНИЕ

Воспользуемся разложением (4):

Преобразуем выражение для данной функции:

Заменим в разложении (4) на () и подставим: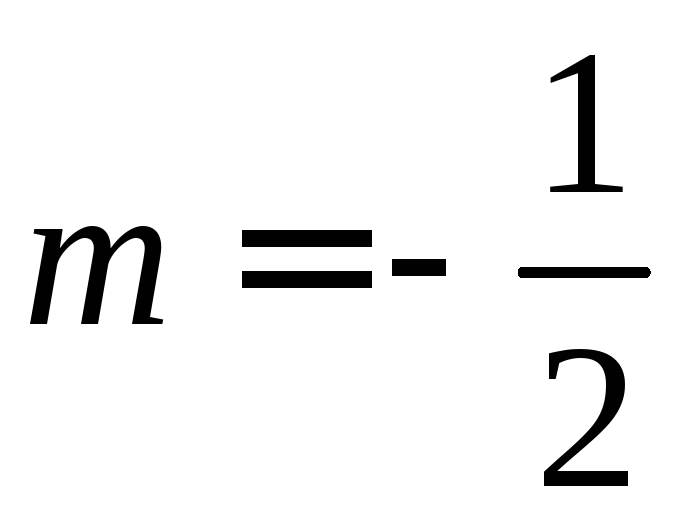

Т.к. для разложения (4) область сходимости , то для того, чтобы найти область сходимости полученного ряда, решим неравенство. Умножим обе части неравенства на (-4), тогда:.

Этот интервал является областью сходимости полученного ряда.

ТАБЛИЦА 2