
- •Федеральное агентство по образованию
- •М. М. Афанасьева, о.С. Громова, в. А. Павский
- •В 3-х частях
- •Часть 2
- •Isb n 5-89289-216-6
- •Правила выполнения и оформления контрольных работ
- •Тема 1. Функции нескольких переменных
- •1.1 Общие сведения
- •1.2 Производные и дифференциалы
- •1.3 Экстремумы функции нескольких переменных
- •1.4 Скалярное поле. Производная по направлению. Градиент
- •Тема 2. Комплексные числа
- •Комплексная плоскость
- •Действия над комплексными числами
- •Тема 3. ОпределенныЙ и неопределенный интегралы
- •3.1 Основные понятия и теоремы Задача, приводящая к понятию определенного интеграла
- •Определенный интеграл
- •I этап.
- •Связь интегрирования с дифференцированием
- •Неопределенный интеграл
- •Формула ньютона-лейбница
- •, Где .
- •Свойства интегралов
- •Метод интегрирования по частям
- •3.3 Основные классы интегрируемых функций
- •Интегрирование рациональных функций
- •1 Случай.
- •2 Случай.
- •3 Случай.
- •Интегрирование иррациональных функций
- •Интегрирование тригонометрических функций
- •3.4 Несобственные интегралы
- •Несобственный интеграл с бесконечными пределами
- •Несобственный интеграл от неограниченной функции
- •3.5 Приложения интегрального исчисления к геометрии Применение определенных интегралов к вычислению площадей
- •Вычисление длины дуги плоской кривой
- •Вычисление объёмов
- •Тема 4. Дифференциальные уравнения
- •4.1 Основные понятия
- •4.2 Дифференциальные уравнения 1-го порядка
- •Дифференциальные уравнения с разделёнными переменными
- •Дифференциальные уравнения с разделяющимися переменными
- •Однородные дифференциальные уравнения 1-го порядка
- •Линейные дифференциальные уравнения 1-го порядка
- •4.3 Дифференциальные уравнения второго порядка
- •Дифференциальные уравнения 2-го порядка, допускающие понижение порядка
- •Линейные дифференциальные уравнения второго порядка
- •Линейные уравнения 2-го порядка с постоянными коэффициентами
- •4.4 Задачи на составление дифференциальных уравнений
- •Тема 5. Ряды
- •5.1 Числовые ряды
- •5.2 Числовые ряды с положительными членами
- •Интегральный признак Коши
- •Первый признак сравнения
- •Второй признак сравнения
- •Признак Даламбера
- •5.3 Знакопеременные ряды
- •Знакопеременные ряды. Абсолютная и условная сходимость
- •Достаточный признак сходимости
- •5.4 Степенные ряды
- •Теорема Абеля
- •Свойства степенных рядов
- •5.5 Разложение функции в степенной ряд. Ряд Тейлора
- •Разложение по степеням X некоторых элементарных функций
- •5.6 Применение степенных рядов Интегрирование функций
- •Интегрирование дифференциальных уравнений
- •Контрольные задания
- •9. . 10..
Метод интегрирования по частям
Иногда
при интегрировании имеет смысл представить
подынтегральное выражение как произведение
некоторой функции
![]() на дифференциал другой функции
на дифференциал другой функции![]() .
Метод интегрирования по частям следует
из формулы дифференцирования произведения
двух функций.
.
Метод интегрирования по частям следует
из формулы дифференцирования произведения
двух функций.
Формула интегрирования по частям в неопределенном интеграле
![]() .
.
ДОКАЗАТЕЛЬСТВО
Пусть
![]() и
и![]() - дифференцируемые функции от переменной
- дифференцируемые функции от переменной![]() .
Найдем дифференциал их произведения
.
Найдем дифференциал их произведения
![]() ,
,
а затем проинтегрируем полученное выражение
![]() .
.
Или
![]() ,
, ![]() .
.
ПРИМЕР. Вычислить
![]() .
.
РЕШЕНИЕ
Примем
за функцию
![]() ,
а за дифференциал
,
а за дифференциал![]() ,
тогда
,
тогда
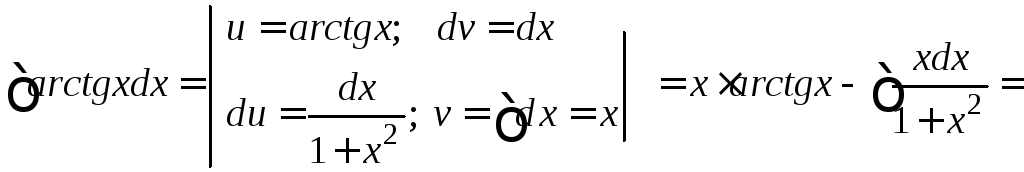
 .
.
ПРИМЕР. Вычислить ![]() .
.
РЕШЕНИЕ

 .
.
Формула интегрирования по частям в определенном интеграле
 .
.
ДОКАЗАТЕЛЬСТВО
Проинтегрируем
выражение
![]() на промежутке
на промежутке![]()
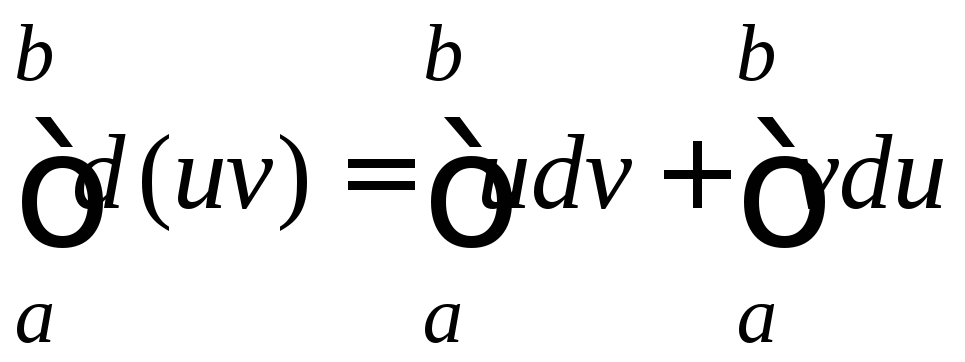 ,
и, выразив
,
и, выразив![]() ,
получим
,
получим
 ,
,  ,
,
 .
.
ПРИМЕР.
Вычислить  .
.
РЕШЕНИЕ

 .
.
Рассмотренные методы применяются при интегрировании основных классов функции.
3.3 Основные классы интегрируемых функций

Интегрирование рациональных функций
Рассмотрим
интеграл от рациональной функции
![]() .
.
Целая
рациональная
функция представляет собой многочлен
степени n,
общий вид которого: ![]() .
.
Тогда:
![]() .
.
ПРИМЕР. Вычислить
неопределенный интеграл ![]() .
.
РЕШЕНИЕ
 .
.
Дробно-рациональная
функция представляет собой отношение
многочленов, т.е.  ,
здесь
,
здесь![]() и
и![]() - многочлены степени
- многочлены степени![]() и
и![]() соответственно.
соответственно.
Если
степень многочлена в числителе
![]() меньше степени многочлена в знаменателе
меньше степени многочлена в знаменателе![]() ,
тодробь
называют правильной
,
тодробь
называют правильной
![]() ,
если
,
если![]() -неправильной.
-неправильной.
Всякую дробно-рациональную функцию можно представить в виде суммы целой части, если дробь неправильная, и простых рациональных дробей. Целая часть, т. е. многочлен, интегрируется почленно. Интегрирование простых дробей рассмотрим ниже.
К простым дробям относят дроби вида:
1.
![]() , 2.
, 2. (
(![]() ),
),
3.
 , 4.
, 4. (
(![]() ),
),
здесь
![]() - постоянные коэффициенты, а квадратный
трехчлен
- постоянные коэффициенты, а квадратный
трехчлен![]() не имеет действительных корней.
не имеет действительных корней.
Найдем интегралы для первых трех видов дробей:
1.  .
.
2.
 .
.
3.  .
.
Выделим в числителе производную знаменателя и представим интеграл в виде суммы двух интегралов, т.е.

 применим
формулу
применим
формулу
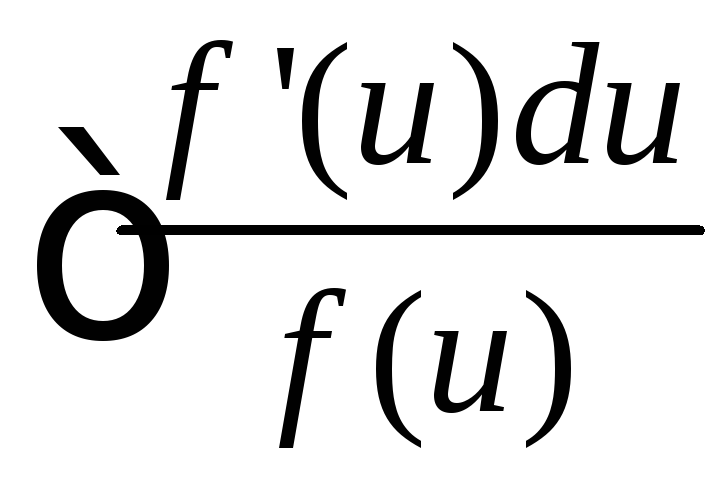

 выделим
полный квадрат
выделим
полный квадрат


сводится к табличному
Приемы интегрирования простых дробей четвертого типа можно найти в дополнительной литературе.
Разложение
правильной дроби на простые дроби
связано с разложением её знаменателя
![]() на простые
множители.
на простые
множители.
1 Случай.
Рассмотрим
рациональную функцию
 ,
знаменатель которой можно разложить в
виде:
,
знаменатель которой можно разложить в
виде:
![]() ,
,
тогда дробь можно представить в виде суммы простейших дробей первого типа:
 ,
,
где
![]() неизвестные коэффициенты, которые можно
найти методом неопределенных коэффициентов
(см. пример ниже).
неизвестные коэффициенты, которые можно
найти методом неопределенных коэффициентов
(см. пример ниже).
После этого интеграл можно представить в виде суммы интегралов
 .
.
ПРИМЕР. Найти  .
.
РЕШЕНИЕ
1 шаг. Согласно теореме дробь можно разложить на сумму простых дробей:
 .
.
2
шаг. Методом
неопределенных коэффициентов
найдем неизвестные числа
![]() .
Для этого приведем дроби в правой части
равенства к общему знаменателю и
приравняем числители полученных дробей:
.
Для этого приведем дроби в правой части
равенства к общему знаменателю и
приравняем числители полученных дробей:
![]() .
.
Сгруппируем
члены с одинаковыми степенями
![]() :
:
![]() .
.
Приравняем
коэффициенты при одинаковых степенях
![]() в левой и правой частях тождества и
получим систему из двух уравнений:
в левой и правой частях тождества и
получим систему из двух уравнений:
 откуда
откуда 
3 шаг. Представим дробь в виде суммы простейших дробей

и найдем интеграл
 .
.
