
- •Федеральное агентство по образованию
- •М. М. Афанасьева, о.С. Громова, в. А. Павский
- •В 3-х частях
- •Часть 2
- •Isb n 5-89289-216-6
- •Правила выполнения и оформления контрольных работ
- •Тема 1. Функции нескольких переменных
- •1.1 Общие сведения
- •1.2 Производные и дифференциалы
- •1.3 Экстремумы функции нескольких переменных
- •1.4 Скалярное поле. Производная по направлению. Градиент
- •Тема 2. Комплексные числа
- •Комплексная плоскость
- •Действия над комплексными числами
- •Тема 3. ОпределенныЙ и неопределенный интегралы
- •3.1 Основные понятия и теоремы Задача, приводящая к понятию определенного интеграла
- •Определенный интеграл
- •I этап.
- •Связь интегрирования с дифференцированием
- •Неопределенный интеграл
- •Формула ньютона-лейбница
- •, Где .
- •Свойства интегралов
- •Метод интегрирования по частям
- •3.3 Основные классы интегрируемых функций
- •Интегрирование рациональных функций
- •1 Случай.
- •2 Случай.
- •3 Случай.
- •Интегрирование иррациональных функций
- •Интегрирование тригонометрических функций
- •3.4 Несобственные интегралы
- •Несобственный интеграл с бесконечными пределами
- •Несобственный интеграл от неограниченной функции
- •3.5 Приложения интегрального исчисления к геометрии Применение определенных интегралов к вычислению площадей
- •Вычисление длины дуги плоской кривой
- •Вычисление объёмов
- •Тема 4. Дифференциальные уравнения
- •4.1 Основные понятия
- •4.2 Дифференциальные уравнения 1-го порядка
- •Дифференциальные уравнения с разделёнными переменными
- •Дифференциальные уравнения с разделяющимися переменными
- •Однородные дифференциальные уравнения 1-го порядка
- •Линейные дифференциальные уравнения 1-го порядка
- •4.3 Дифференциальные уравнения второго порядка
- •Дифференциальные уравнения 2-го порядка, допускающие понижение порядка
- •Линейные дифференциальные уравнения второго порядка
- •Линейные уравнения 2-го порядка с постоянными коэффициентами
- •4.4 Задачи на составление дифференциальных уравнений
- •Тема 5. Ряды
- •5.1 Числовые ряды
- •5.2 Числовые ряды с положительными членами
- •Интегральный признак Коши
- •Первый признак сравнения
- •Второй признак сравнения
- •Признак Даламбера
- •5.3 Знакопеременные ряды
- •Знакопеременные ряды. Абсолютная и условная сходимость
- •Достаточный признак сходимости
- •5.4 Степенные ряды
- •Теорема Абеля
- •Свойства степенных рядов
- •5.5 Разложение функции в степенной ряд. Ряд Тейлора
- •Разложение по степеням X некоторых элементарных функций
- •5.6 Применение степенных рядов Интегрирование функций
- •Интегрирование дифференциальных уравнений
- •Контрольные задания
- •9. . 10..
Второй признак сравнения
Если
существует конечный отличный от нуля
предел
 (если
(если![]() ),
то оба ряда сходятся или оба расходятся
одновременно.
),
то оба ряда сходятся или оба расходятся
одновременно.
ДОКАЗАТЕЛЬСТВО
Пусть
ряд (2) сходится и
![]() .
Взяв произвольное число
.
Взяв произвольное число![]() ,
для достаточно больших номеров
,
для достаточно больших номеров![]() будем иметь
будем иметь или
или .
Из неравенства
.
Из неравенства следует, что
следует, что![]() .
В силу свойств сходящихся рядов
одновременно с рядом (2) будет сходиться
и ряд
.
В силу свойств сходящихся рядов
одновременно с рядом (2) будет сходиться
и ряд ,
полученный умножением его членов на
число
,
полученный умножением его членов на
число![]() .
Отсюда, по первому признаку сравнения,
вытекает сходимость ряда (1).
.
Отсюда, по первому признаку сравнения,
вытекает сходимость ряда (1).
Если
же ряд (2) расходится, то из неравенства
 или
или![]() следует, что ряд (1) также расходится.
следует, что ряд (1) также расходится.
Трудность
применения на практике признаков
сравнения состоит в необходимости иметь
“запас” рядов, сходимость (или
расходимость) которых известна. В
качестве «эталонных» рядов, обычно
используются ряды, образованные членами
геометрической прогрессии, или обобщенный
гармонический
ряд  .
.
ПРИМЕР. Исследовать
на сходимость числовой ряд
 .
.
РЕШЕНИЕ
Сравним данный ряд с рядом
 .
.
Ряд
![]() сходится, т.к. его члены образуют
бесконечно убывающую геометрическую
прогрессию со знаменателем
сходится, т.к. его члены образуют
бесконечно убывающую геометрическую
прогрессию со знаменателем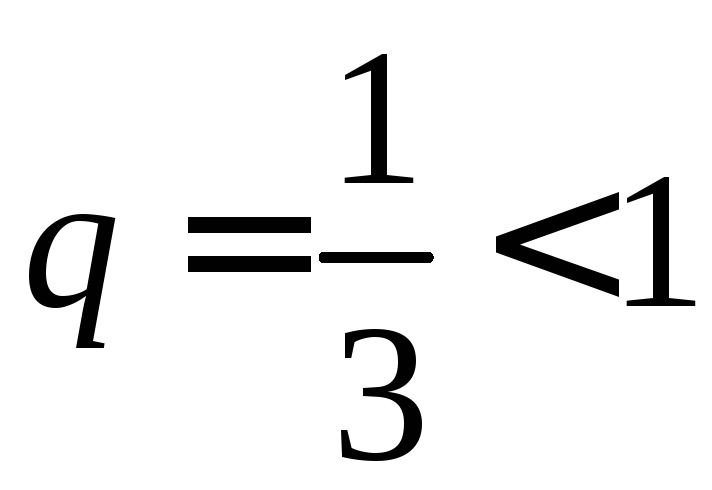 .
Каждый член исследуемого ряда меньше
соответствующего члена ряда
.
Каждый член исследуемого ряда меньше
соответствующего члена ряда![]() :
:

поэтому, согласно первому признаку сравнения, ряд сходится.
ПРИМЕР.
Исследовать на сходимость ряд

РЕШЕНИЕ
Сравним
этот ряд с гармоническим рядом  Ряд (*) расходится (p=1).
Применим для исследования ряда второй
признак сравнения:
Ряд (*) расходится (p=1).
Применим для исследования ряда второй
признак сравнения:
 .
.
Предел конечен и не равен нулю. Поэтому, согласно второму признаку сравнения, т.к. расходится ряд (*), то расходится и исследуемый ряд.
ПРИМЕР. Исследовать
на сходимость ряд  .
.
РЕШЕНИЕ
Сравним
его с рядом
 ,
общий член, которого
,
общий член, которого .
Этот ряд сходится, т.к.
.
Этот ряд сходится, т.к.![]() Применим второй признак сравнения:
Применим второй признак сравнения:

 .
.
Т.к. этот предел конечен и не равен нулю, а ряд, с которым мы сравнивали, сходящийся, то, согласно второму признаку сравнения, исследуемый ряд тоже сходится.
Признак Даламбера
Пусть
для числового ряда с положительными
членами
 ,
,![]() существует предел
существует предел ,
,
то при l<1 ряд сходится, при l>1 ряд расходится, при l=1 вопрос о сходимости ряда остается нерешенным (надо применить другой признак).
ДОКАЗАТЕЛЬСТВО
По
определению предела для любого
![]() существует
существует![]() ,
что для любого
,
что для любого![]() выполняется соотношение
выполняется соотношение
 или
или  .
.
1).
Пусть
![]() .
Выберем
.
Выберем![]() так, чтобы число
так, чтобы число![]() .
Тогда, если
.
Тогда, если![]()
 ,
,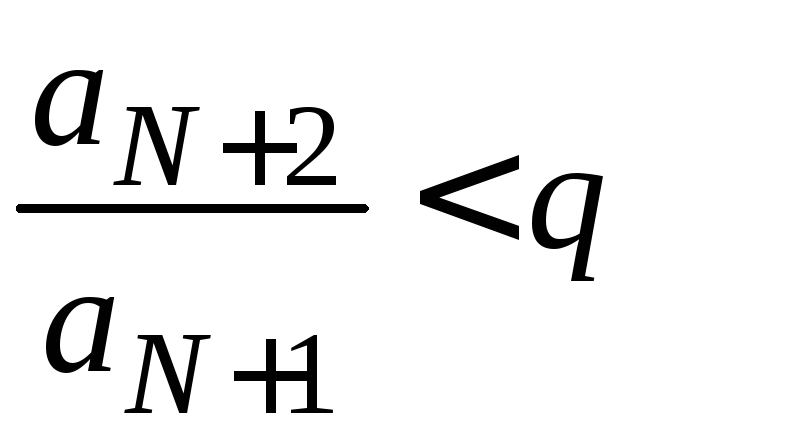 и т. д. Отсюда получим, что
и т. д. Отсюда получим, что
![]() ,
,![]() ,
,![]() ,....
,....
Ряд
![]() сходится, так как члены ряда образуют
геометрическую прогрессию со знаменателем
сходится, так как члены ряда образуют
геометрическую прогрессию со знаменателем![]() .
Тогда по первому признаку сравнения
ряд
.
Тогда по первому признаку сравнения
ряд
![]()
также
сходится. Этот ряд получен из ряда
 после отбрасывания первых
после отбрасывания первых![]() членов (остаток ряда). Значит, ряд
членов (остаток ряда). Значит, ряд сходится (свойство 3).
сходится (свойство 3).
2).
Пусть
![]() .
Тогда, начиная с некоторого номера,
.
Тогда, начиная с некоторого номера,![]() будет выполняться неравенство
будет выполняться неравенство (если выбрать
(если выбрать![]() достаточно малым).
достаточно малым).
Из
этого неравенства следует, что каждый
последующий член ряда будет больше
предыдущего
![]() ,
а т.к. они положительны, то предел общего
члена ряда не может быть равен нулю.
Следовательно, в силу необходимого
признака сходимости, ряд расходится.
,
а т.к. они положительны, то предел общего
члена ряда не может быть равен нулю.
Следовательно, в силу необходимого
признака сходимости, ряд расходится.
3).
Пусть l=1.
Возьмем два известных ряда:  .
.
В
том и другом случае
 ,
но при этом один ряд сходится, а другой
расходится. Поэтому в случае, когда этот
предел равен 1, необходимо применять
другой признак для решения вопроса о
сходимости ряда.
,
но при этом один ряд сходится, а другой
расходится. Поэтому в случае, когда этот
предел равен 1, необходимо применять
другой признак для решения вопроса о
сходимости ряда.
ПРИМЕР.
Исследовать на сходимость ряд числовой  .
.
РЕШЕНИЕ
Общий
член этого ряда имеет вид
 .
.
Для
того чтобы найти
![]() й
член ряда
й
член ряда
![]() ,
вместоn
в выражение
,
вместоn
в выражение
![]() подставимn+1:
подставимn+1:
 .
.
Вычислим предел
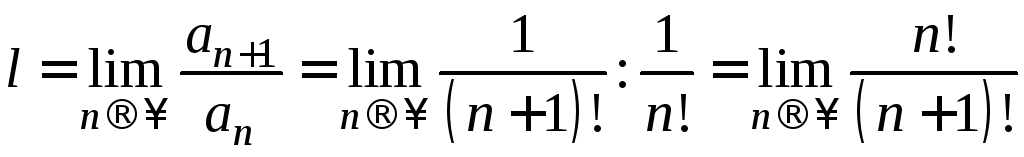 .
.
Т.к.
![]() ,
а
,
а![]() то после сокращения получим
то после сокращения получим
 .
.
По
признаку Даламбера, если
![]() то ряд сходится.
то ряд сходится.
ПРИМЕР.
Исследовать на сходимость числовой
ряд  .
.
РЕШЕНИЕ.
Общий
член ряда
 . Запишем
последующий член ряда
. Запишем
последующий член ряда .
Найдем предел отношения
.
Найдем предел отношения

 .
.
Т.к.
![]() то по признаку Даламбера ряд расходится.
то по признаку Даламбера ряд расходится.
