2 Случай.

Пусть знаменатель дроби можно представить в виде:

.

Тогда дробь можно записать в виде суммы простых дробей следующим образом:

.

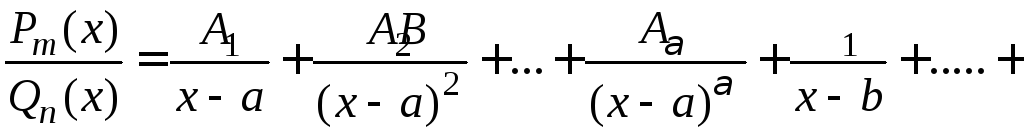
Интеграл от этой рациональной дроби будет равен сумме интегралов от каждой из простых дробей.

ПРИМЕР. Найти .

РЕШЕНИЕ

1 шаг. Знаменатель дроби имеет кратный корень (кратность корня равна 2), поэтому в разложении дроби записывают две простые дроби. Неизвестные коэффициенты находят методом неопределенных коэффициентов

.

2 шаг.

.

Приравняем коэффициенты при одинаковых степенях и свободные члены, получим системуоткуда

3 шаг. Подставим ив разложение и найдем интеграл

,

.

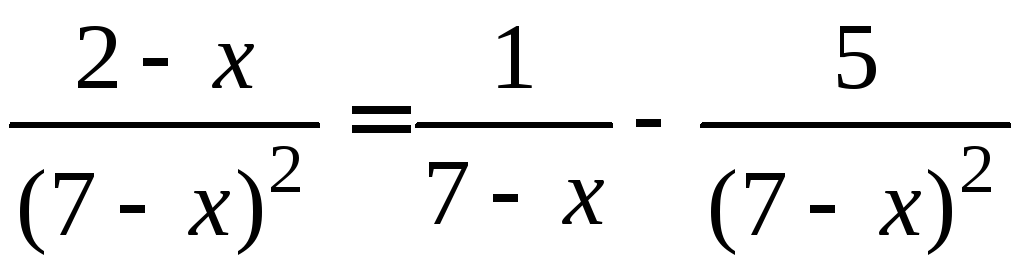3 Случай.

Знаменатель правильной рациональной дроби представлен в виде произведения квадратных трехчленов, не имеющих действительных корней:

_.

Тогда дробь может быть представлена в виде:

.

Чтобы найти интеграл от такой дроби, надо найти интеграл от каждой из дробей, содержащих в знаменателе квадратный трехчлен.

ПРИМЕР. Найти .

РЕШЕНИЕ

1 шаг. Квадратные трехчлены ине имеют действительных корней. Запишем разложение дроби на сумму простейших дробей и приведем дроби в правой части равенства к общему знаменателю

.

2 шаг. Приравняем числители дробей и составим систему уравнений:

.

отсюда

3 шаг. Найдем интеграл от дроби

,

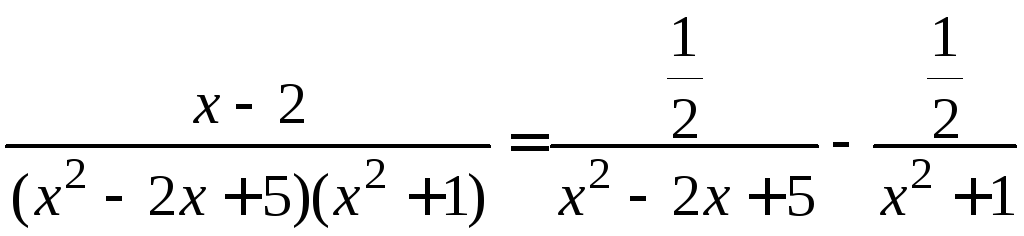выделим полный квадрат

.

Интегрирование иррациональных функций

Задача состоит в том, чтобы с помощью подстановки свести интеграл от иррациональной функции к интегралу от рациональной функции.

Рассмотрим некоторые из видов иррациональных функций.

1. , где– рациональная функция своих аргументов;дробные показатели.

Чтобы перейти к интегрированию рациональной функции, введем подстановку , где– НОК (наименьшее общее кратное) знаменателей дробей.

ПРИМЕР. Найти .

РЕШЕНИЕ

В данной функции дробные показатели степени. Их знаменатели 2 и 3, НОК(2,3)=6, следовательно, можно сделать подстановку. Тогда

.

2. , где- рациональная функция своих аргументов,n – натуральное число.

В этом случае вводится подстановка . Таким образом, переходим к интегрированию дробно-рациональной функции.

ПРИМЕР. Найти .

РЕШЕНИЕ

Сделаем подстановку , тогда, а.

Получим

.

Интегрирование тригонометрических функций

Пусть дано выражение, зависящее, и притом рационально, только от тригонометрических функций. Так как все тригонометрические функции выражаются через и, то это выражение можно считать рациональной функцией оти. Рассмотрим приёмы интегрирования некоторых из них.

1. Интегралы вида всегда могут быть рационализированы с помощью подстановки.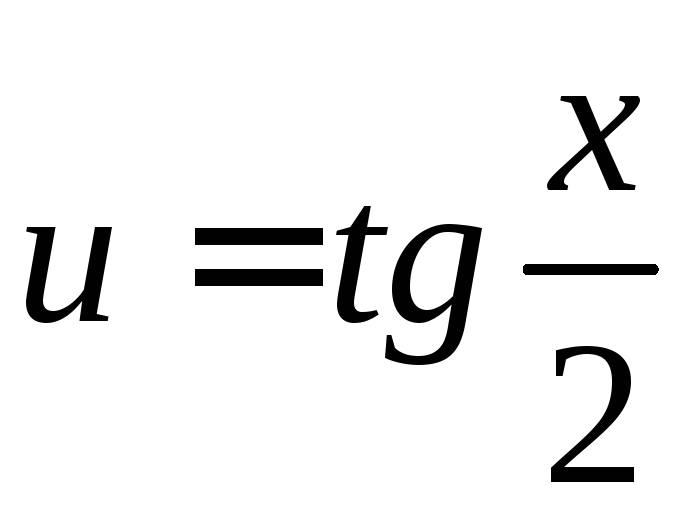

Тогда .

ПРИМЕР. Найти интеграл .

РЕШЕНИЕ

Сделаем подстановку и подставим в интеграл соотношенияи.

Получим .

2. Интегралы ,илегко вычисляются, если преобразовать произведение тригонометрических функций в сумму.

ПРИМЕР. Вычислить интеграл .

РЕШЕНИЕ

Воспользуемся формулой

.

Тогда

.

3. При нахождении интегралов вида используют различные приемы в зависимости от показателейи.

ПРИМЕР. Найти .

РЕШЕНИЕ

Если ицелые числа, и хотя бы одно из них положительное и нечетное, то подстановка(еслии нечетное) или(еслии нечетное) приводит к интегрированию степенных функций.

В данном случае , поэтому сделаем подстановку. Тогдаи интеграл примет вид:

.

ПРИМЕР. Найти интеграл .

РЕШЕНИЕ

Если оба показателя иположительные и четные, то применяются тригонометрические формулы

.

.

Изученные нами методы интегрирования состоят в преобразованиях, приводящих интеграл к заранее известному интегралу, т. е. находящемуся в таблице интегралов. До сих пор мы пользовались краткой – основной-таблицей интегралов. На практике часто используются различные справочники и таблицы часто встречающихся интегралов.

В отличие от дифференцирования, операция интегрирования непрерывных функций не всегда позволяет найти элементарную функцию, являющуюся первообразной для заданной функции. Доказано, что всякая непрерывная функция имеет первообразную, но существуют такие элементарные функции, интегралы от которых не выражаются никакими конечными комбинациями основных элементарных функций или имеют весьма сложный и неудобный для вычислений вид. Такие интегралы называют “неберущимися”. Например, интегралы

,

нельзя представить никакой конечной комбинацией элементарных функций. В этих случаях применяются различные способы приближённого вычисления интегралов.