
- •Федеральное агентство по образованию
- •М. М. Афанасьева, о.С. Громова, в. А. Павский
- •В 3-х частях
- •Часть 2
- •Isb n 5-89289-216-6
- •Правила выполнения и оформления контрольных работ
- •Тема 1. Функции нескольких переменных
- •1.1 Общие сведения
- •1.2 Производные и дифференциалы
- •1.3 Экстремумы функции нескольких переменных
- •1.4 Скалярное поле. Производная по направлению. Градиент
- •Тема 2. Комплексные числа
- •Комплексная плоскость
- •Действия над комплексными числами
- •Тема 3. ОпределенныЙ и неопределенный интегралы
- •3.1 Основные понятия и теоремы Задача, приводящая к понятию определенного интеграла
- •Определенный интеграл
- •I этап.
- •Связь интегрирования с дифференцированием
- •Неопределенный интеграл
- •Формула ньютона-лейбница
- •, Где .
- •Свойства интегралов
- •Метод интегрирования по частям
- •3.3 Основные классы интегрируемых функций
- •Интегрирование рациональных функций
- •1 Случай.
- •2 Случай.
- •3 Случай.
- •Интегрирование иррациональных функций
- •Интегрирование тригонометрических функций
- •3.4 Несобственные интегралы
- •Несобственный интеграл с бесконечными пределами
- •Несобственный интеграл от неограниченной функции
- •3.5 Приложения интегрального исчисления к геометрии Применение определенных интегралов к вычислению площадей
- •Вычисление длины дуги плоской кривой
- •Вычисление объёмов
- •Тема 4. Дифференциальные уравнения
- •4.1 Основные понятия
- •4.2 Дифференциальные уравнения 1-го порядка
- •Дифференциальные уравнения с разделёнными переменными
- •Дифференциальные уравнения с разделяющимися переменными
- •Однородные дифференциальные уравнения 1-го порядка
- •Линейные дифференциальные уравнения 1-го порядка
- •4.3 Дифференциальные уравнения второго порядка
- •Дифференциальные уравнения 2-го порядка, допускающие понижение порядка
- •Линейные дифференциальные уравнения второго порядка
- •Линейные уравнения 2-го порядка с постоянными коэффициентами
- •4.4 Задачи на составление дифференциальных уравнений
- •Тема 5. Ряды
- •5.1 Числовые ряды
- •5.2 Числовые ряды с положительными членами
- •Интегральный признак Коши
- •Первый признак сравнения
- •Второй признак сравнения
- •Признак Даламбера
- •5.3 Знакопеременные ряды
- •Знакопеременные ряды. Абсолютная и условная сходимость
- •Достаточный признак сходимости
- •5.4 Степенные ряды
- •Теорема Абеля
- •Свойства степенных рядов
- •5.5 Разложение функции в степенной ряд. Ряд Тейлора
- •Разложение по степеням X некоторых элементарных функций
- •5.6 Применение степенных рядов Интегрирование функций
- •Интегрирование дифференциальных уравнений
- •Контрольные задания
- •9. . 10..
4.2 Дифференциальные уравнения 1-го порядка
В
общем виде дифференциальное уравнение
1-го порядка можно записать как
равенство ![]() .
.
Если
уравнение разрешено относительно
производной
![]() ,
то оно приобретает вид:
,
то оно приобретает вид:![]()
или
в дифференциальной форме ![]() .
.
Общее
решение дифференциального уравнения
1-го порядка может быть записано в неявном
![]() и явном
и явном![]() видах. И, так как в нем присутствует одна
произвольная постоянная, то для нахождения
частного решения необходимо задать
одно начальное условие:
видах. И, так как в нем присутствует одна
произвольная постоянная, то для нахождения
частного решения необходимо задать
одно начальное условие:![]() .
.
График
частного решения представляет собой
линию, проходящую через точку с
координатами
![]() .
Эта линия называетсяинтегральной
кривой.
.
Эта линия называетсяинтегральной
кривой.
Вопрос о том, в каком случае можно утверждать, что частное решение дифференциального уравнения, удовлетворяющее данному начальному условию, существует и единственно, решает следующая теорема.
ТЕОРЕМА (существования и единственности решения)
Если
функция
![]() непрерывна в области, содержащей точку
непрерывна в области, содержащей точку![]() ,
то уравнение
,
то уравнение![]() имеет решение
имеет решение![]() такое,
такое,
что
![]() .
Если,
кроме того, непрерывна и частная
производная
.
Если,
кроме того, непрерывна и частная
производная
![]() ,
то это решение единственно.
,
то это решение единственно.
Рассмотрим несколько наиболее часто встречающихся видов дифференциальных уравнений 1-го порядка.
Дифференциальные уравнения с разделёнными переменными
ОПРЕДЕЛЕНИЕ. Дифференциальное уравнение вида
![]()
называют
уравнением с разделенными переменными.
Функции
![]() и
и![]() будем считать непрерывными.
будем считать непрерывными.
Произведем
интегрирование и получим связь между
переменными
![]() и
и![]() ,
освобожденную от их дифференциалов
,
освобожденную от их дифференциалов
![]() ,
,
т. е. функцию, которая является общим решением исходного уравнения.
ПРИМЕР. Найти
общее решение уравнения ![]() .
.
РЕШЕНИЕ.
Запишем
уравнение в виде ![]() .
.![]() Переменные
разделены, так как множитель перед
дифференциалом
Переменные
разделены, так как множитель перед
дифференциалом![]() является функцией только от переменной
является функцией только от переменной![]() ,
а множитель перед
,
а множитель перед![]() функцией только от переменной
функцией только от переменной![]() .
Интегрируя обе части уравнения, получим
.
Интегрируя обе части уравнения, получим
![]() или
или  .
.
Если
умножить уравнение на 2 и ввести
обозначение
![]() ,
то общее решение можно записать в виде
,
то общее решение можно записать в виде![]() .
.
Интегральными кривыми для исходного уравнения являются окружности с центром в начале координат.
Дифференциальные уравнения с разделяющимися переменными
ОПРЕДЕЛЕНИЕ.
Уравнением
с разделяющимися переменными называется
уравнение вида ![]() .
.
Чтобы
привести это уравнение к уравнению с
разделёнными переменными, достаточно
разделить его на произведение
![]() :
:
 .
.
Тогда
получим уравнение
 ,
которое легко интегрируется:
,
которое легко интегрируется: .
.
Надо
помнить, что деление уравнения на функцию
![]() может привести к потере частных решений,
которые получаются из уравнения
может привести к потере частных решений,
которые получаются из уравнения![]() .
Определяя из этого уравнения решение
.
Определяя из этого уравнения решение![]() ,
следует проверить, является ли оно
решением исходного уравнения. Если не
является, то его нужно отбросить, а если
является, то проверить, входит ли оно в
общее решение, т.е. будет ли оно частным
решением. Если решение не является
частным решением, его называютособым.
,
следует проверить, является ли оно
решением исходного уравнения. Если не
является, то его нужно отбросить, а если
является, то проверить, входит ли оно в
общее решение, т.е. будет ли оно частным
решением. Если решение не является
частным решением, его называютособым.
ПРИМЕР. Найти
общее решение уравнения ![]() .
.
РЕШЕНИЕ
Представим
производную
![]() как
как![]() ,
тогда уравнение можно записать в
дифференциальном виде
,
тогда уравнение можно записать в
дифференциальном виде .
.
Чтобы
разделить переменные, умножим обе части
уравнения на
![]() .
Получим равенство, которое проинтегрируем:
.
Получим равенство, которое проинтегрируем:
![]() ,
, ![]() ,
, .
.
Это и есть общее решение уравнения.
ПРИМЕР. Найти
решение уравнения ![]() .
.
РЕШЕНИЕ
Запишем
уравнение в виде: ![]() .
Теперь заменим
.
Теперь заменим![]() на
на![]() :
:
 .
.
Если
умножить уравнение на
![]() и разделить на
и разделить на![]() ,
то получим уравнение с разделёнными
переменными:
,
то получим уравнение с разделёнными
переменными: .
.
Найдем интегралы от обеих частей равенства:

![]() или
или .
.
Это
общий интеграл (решение) дифференциального
уравнения. Полученную функцию можно
упростить и привести к виду ![]() .
.
Проверим,
является ли частным решением уравнения
функция
![]() .
Подставим
.
Подставим![]() и
и![]() в исходное уравнение:
в исходное уравнение:![]() ,
получим тождество. Следовательно,
функция
,
получим тождество. Следовательно,
функция![]() является решением уравнения. Если общее
решение уравнения записать в виде
является решением уравнения. Если общее
решение уравнения записать в виде![]() ,
то функция
,
то функция![]() получится из него, когда
получится из него, когда![]() ,
т.е. она является частным решением.
,
т.е. она является частным решением.
ПРИМЕР. Найти общий интеграл уравнения (общее решение)
![]()
и
частное решение, удовлетворяющее
начальным условиям:
![]() .
.
РЕШЕНИЕ
Это
уравнение относится к уравнениям с
разделяющимися переменными. Разделим
переменные, для чего обе части уравнения
поделим на
![]() :
:
 .
.
Получим уравнение:
 .
.
Проинтегрируем его:
 ,
,  ,
,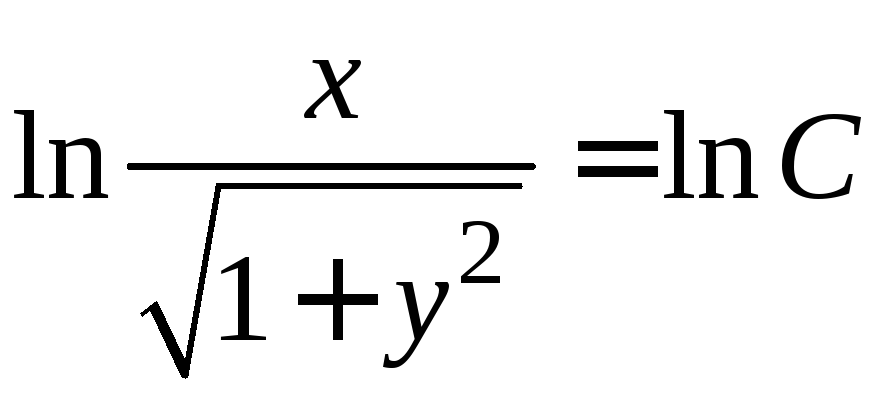 .
.
Константу
![]() для дальнейшего упрощения функций
удобно взять в форме
для дальнейшего упрощения функций
удобно взять в форме![]() .
Таким образом, общий интеграл запишется
в виде
.
Таким образом, общий интеграл запишется
в виде
 .
.
В
этом уравнении при делении на функцию
![]() может быть потеряно решение
может быть потеряно решение![]() .
Но это решение получается из общего
решения, если
.
Но это решение получается из общего
решения, если![]() ,
т.е. является частным решением.
,
т.е. является частным решением.
Найдем
частное решение, удовлетворяющее
начальным условиям
![]() .
Подставим начальные условия в общий
интеграл и найдем значение константы
.
Подставим начальные условия в общий
интеграл и найдем значение константы![]() :
: ,
откуда
,
откуда![]() .
Тогда частное решение запишется в виде:
.
Тогда частное решение запишется в виде:![]() .
.
ПРИМЕР. Найти общий интеграл (общее решение) уравнения
![]()
РЕШЕНИЕ
Убедимся, что это уравнение является уравнением с разделяющимися переменными. Для этого вынесем за скобки общие множители
![]() .
.
Теперь
разделим обе части уравнения на
![]()
 ,
,
и после сокращения получим

Переменные разделены, можно интегрировать:

Найдем каждый интеграл отдельно:
 ,
,

Общий
интеграл (решение) уравнения примет
вид:

Это
выражение можно преобразовать,
воспользовавшись свойством логарифмов,
тогда получим  .
.
