
- •Федеральное агентство по образованию
- •М. М. Афанасьева, о.С. Громова, в. А. Павский
- •В 3-х частях
- •Часть 2
- •Isb n 5-89289-216-6
- •Правила выполнения и оформления контрольных работ
- •Тема 1. Функции нескольких переменных
- •1.1 Общие сведения
- •1.2 Производные и дифференциалы
- •1.3 Экстремумы функции нескольких переменных
- •1.4 Скалярное поле. Производная по направлению. Градиент
- •Тема 2. Комплексные числа
- •Комплексная плоскость
- •Действия над комплексными числами
- •Тема 3. ОпределенныЙ и неопределенный интегралы
- •3.1 Основные понятия и теоремы Задача, приводящая к понятию определенного интеграла
- •Определенный интеграл
- •I этап.
- •Связь интегрирования с дифференцированием
- •Неопределенный интеграл
- •Формула ньютона-лейбница
- •, Где .
- •Свойства интегралов
- •Метод интегрирования по частям
- •3.3 Основные классы интегрируемых функций
- •Интегрирование рациональных функций
- •1 Случай.
- •2 Случай.
- •3 Случай.
- •Интегрирование иррациональных функций
- •Интегрирование тригонометрических функций
- •3.4 Несобственные интегралы
- •Несобственный интеграл с бесконечными пределами
- •Несобственный интеграл от неограниченной функции
- •3.5 Приложения интегрального исчисления к геометрии Применение определенных интегралов к вычислению площадей
- •Вычисление длины дуги плоской кривой
- •Вычисление объёмов
- •Тема 4. Дифференциальные уравнения
- •4.1 Основные понятия
- •4.2 Дифференциальные уравнения 1-го порядка
- •Дифференциальные уравнения с разделёнными переменными
- •Дифференциальные уравнения с разделяющимися переменными
- •Однородные дифференциальные уравнения 1-го порядка
- •Линейные дифференциальные уравнения 1-го порядка
- •4.3 Дифференциальные уравнения второго порядка
- •Дифференциальные уравнения 2-го порядка, допускающие понижение порядка
- •Линейные дифференциальные уравнения второго порядка
- •Линейные уравнения 2-го порядка с постоянными коэффициентами
- •4.4 Задачи на составление дифференциальных уравнений
- •Тема 5. Ряды
- •5.1 Числовые ряды
- •5.2 Числовые ряды с положительными членами
- •Интегральный признак Коши
- •Первый признак сравнения
- •Второй признак сравнения
- •Признак Даламбера
- •5.3 Знакопеременные ряды
- •Знакопеременные ряды. Абсолютная и условная сходимость
- •Достаточный признак сходимости
- •5.4 Степенные ряды
- •Теорема Абеля
- •Свойства степенных рядов
- •5.5 Разложение функции в степенной ряд. Ряд Тейлора
- •Разложение по степеням X некоторых элементарных функций
- •5.6 Применение степенных рядов Интегрирование функций
- •Интегрирование дифференциальных уравнений
- •Контрольные задания
- •9. . 10..
4.3 Дифференциальные уравнения второго порядка
Дифференциальное уравнение 2-го порядка в общем виде можно записать как
![]() или
или ![]() .
.
Общее
решение
и общий
интеграл
уравнения содержат две произвольные
постоянные и задаются формулами
![]() или
или![]() .
.
Частное
решение
уравнения находится, если задать
начальные условия (задача Коши) ![]() .
.
ТЕОРЕМА (существования и единственности решения)
Если
функция
![]() непрерывна в окрестности значений
непрерывна в окрестности значений![]() ,
то уравнение
,
то уравнение![]() имеет решение
имеет решение![]() такое, что
такое, что![]() .
Если, кроме того, непрерывны и частные
производные
.
Если, кроме того, непрерывны и частные
производные![]() и
и![]() ,
то это решение единственно.
,
то это решение единственно.
Дифференциальные уравнения 2-го порядка, допускающие понижение порядка
I.
Рассмотрим дифференциальное уравнение
2-го
порядка, когда правая
часть
уравнения
не содержит
![]() и
и
![]()
![]() .
.
Такое уравнение решается последовательным двукратным интегрированием.
ПРИМЕР. Решить
дифференциальное уравнение ![]() .
.
РЕШЕНИЕ
Последовательно
интегрируя уравнение, найдем сначала
первую производную:![]() ,
а затем саму функцию:
,
а затем саму функцию:![]() .
.
II.
Дифференциальное
уравнение, правая
часть которого не содержит
![]()
![]() ,
,
можно свести к уравнению первого порядка с помощью подстановки:
![]() ,
,

ПРИМЕР. Найти
общее решение уравнения  .
.
РЕШЕНИЕ.
Положим,
 ,
тогда
,
тогда .
Подставим
.
Подставим![]() в уравнение:
в уравнение:
 .
.
Это
линейное уравнение первого порядка
относительно функции
![]() .
Решим его методом Бернулли. Разделим
обе части уравнения на множитель
.
Решим его методом Бернулли. Разделим
обе части уравнения на множитель![]()

и
будем искать
![]() в виде
в виде![]() .
Тогда
.
Тогда![]() .
Подставим
.
Подставим![]() в уравнение:
в уравнение:
 ,
,  .
.
Составим
систему уравнений 
1
этап: решим
первое уравнение системы и найдем
функцию
![]() :
: 



Тогда ![]() ,
откуда
,
откуда![]() .
.
2
этап: подставим
полученное выражение для функции
![]() во второе уравнение системы и найдем
функцию
во второе уравнение системы и найдем
функцию![]() :
:




Вычислим
интегралы, входящие в левую и правую
части уравнения
![]()


Тогда
получим  .
.
3
этап: т.к. ![]() то
то
4
этап: поскольку
 то получим уравнение
то получим уравнение или
или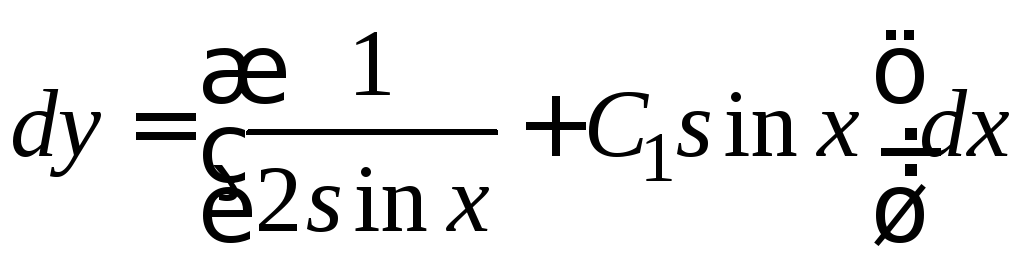 ,
, ,
, ,
,
Это общее решение исходного уравнения.
Дифференциальное уравнение второго порядка, не содержащее явным образом независимой переменной
 ,
т.е. уравнение вида
,
т.е. уравнение вида
![]() .
.
Это
уравнения можно привести к уравнению
1-го порядка с помощью подстановки
![]() .
Тогда по правилу дифференцирования
сложной функции
.
Тогда по правилу дифференцирования
сложной функции .
.
ПРИМЕР. Найти
общий интеграл уравнения ![]() .
.
РЕШЕНИЕ
Уравнение
не содержит явным образом независимую
переменную
![]() ,
поэтому введем новую переменную
,
поэтому введем новую переменную .
Тогда
.
Тогда .
Подставим
.
Подставим![]() и
и![]() в уравнение и получим:
в уравнение и получим:![]() .
Уравнение распадается на два:
.
Уравнение распадается на два:![]() и
и![]() .
.
Из
первого уравнения следует, что
![]() или
или![]() .
.
Второе
уравнение с разделяющимися
переменными: 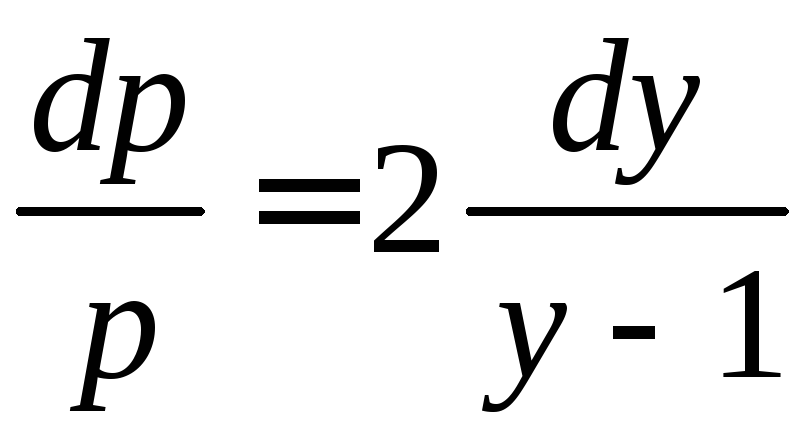 .
.
Общий
интеграл уравнения
![]() .
Применим свойства логарифмов и получим,
что
.
Применим свойства логарифмов и получим,
что![]() .
Тогда
.
Тогда![]() .
Подставим в решение
.
Подставим в решение и получим, что
и получим, что![]() .
.
Вновь пришли к уравнению с разделяющимися переменными:
 .
.
Тогда общий интеграл исходного уравнения имеет вид
 и
и
![]() .
.
Линейные дифференциальные уравнения второго порядка
ОПРЕДЕЛЕНИЕ. Линейным дифференциальным уравнением второго порядка называется уравнение вида
![]() , (*)
, (*)
где
![]() -
функции непрерывные на некотором
промежутке
-
функции непрерывные на некотором
промежутке![]() .
.
Это уравнение называется уравнением с правой частью или неоднородным.
Если
![]() то уравнение имеет вид
то уравнение имеет вид
![]() (**)
(**)
и называется уравнением без правой части или однородным.
ТЕОРЕМА
1. Если
функции
![]() - линейно независимые частные решения
однородного линейного уравнения, то их
линейная комбинация
- линейно независимые частные решения
однородного линейного уравнения, то их
линейная комбинация![]() является общим решением того же уравнения.
Здесь
является общим решением того же уравнения.
Здесь![]() - произвольные постоянные.
- произвольные постоянные.
Замечание:
функции
![]() называются линейно независимыми, если
их отношение не равно постоянной
величине, т.е.
называются линейно независимыми, если
их отношение не равно постоянной
величине, т.е.
ДОКАЗАТЕЛЬСТВО
Продифференцировав
дважды функцию
![]() :
: ![]() ,
,![]() и
подставив
и
подставив
![]() и
и![]() в левую часть уравнения
в левую часть уравнения![]() ,
получим:
,
получим:
![]()
![]() .
.
Так
как функции
![]() и
и![]() по условию теоремы есть решения уравнения,
то выражения в скобках тождественно
равны нулю. Таким образом, функция
по условию теоремы есть решения уравнения,
то выражения в скобках тождественно
равны нулю. Таким образом, функция![]() удовлетворяет исходному уравнению, а
поскольку она зависит от двух произвольных
постоянных, то является общим решением
уравнения.
удовлетворяет исходному уравнению, а
поскольку она зависит от двух произвольных
постоянных, то является общим решением
уравнения.
ТЕОРЕМА
2. Общее
решение неоднородного линейного
уравнения равно сумме его частного
решения и общего решения соответствующего
однородного уравнения, т.е.
![]() .
.
Здесь
![]() - общее решение неоднородно уравнения;
- общее решение неоднородно уравнения;![]() -
общее решение однородного уравнения;
-
общее решение однородного уравнения;![]() -
частное решение неоднородного уравнения.
-
частное решение неоднородного уравнения.
ДОКАЗАТЕЛЬСТВО
Обозначим
через
![]() общее решение однородного уравнения
общее решение однородного уравнения![]() ,
а через
,
а через![]() - какое-нибудь частное решение неоднородного
уравнения
- какое-нибудь частное решение неоднородного
уравнения![]() .
.
Рассмотрим
функцию ![]() .
Имеем
.
Имеем![]() ,
,![]() .
.
Подставляя
выражения для
![]() в левую часть уравнения (*), получим:
в левую часть уравнения (*), получим:
![]()
![]() .
.
Выражение
в первой квадратной скобке равно нулю,
т. к.
![]() - решение однородного уравнения
- решение однородного уравнения![]() ,
а выражение во второй квадратной скобке
равно
,
а выражение во второй квадратной скобке
равно![]() ,
т. к.
,
т. к.![]() - решение неоднородного уравнения
- решение неоднородного уравнения![]() .
Следовательно, функция
.
Следовательно, функция![]() есть решение уравнения
есть решение уравнения![]() .
Так как это решение зависит от двух
произвольных постоянных, то оно и есть
общее решение уравнения.
.
Так как это решение зависит от двух
произвольных постоянных, то оно и есть
общее решение уравнения.
