III. Линейные пространства

Ранее отмечалось, что многие множества, существенно различаясь по природе своих элементов, имеют одинаковые свойства, то есть могут быть описаны, с точки зрения современной алгебры, единой системой аксиом. Наиболее востребован практикой оказался класс множеств, обладающих свойствами линейного пространства. Часто их называют векторными, поскольку векторные величины получили широкое распространение в различных научно-практических исследованиях и приложениях. Кроме того, векторные пространства геометрически наглядны, что делает линейные пространства понятными, расширяя тем самым область использования их в науке и практических исследованиях.

Во введении понятие числового поля определялось аксиоматически. Рассмотрены поля рациональных чисел Q, действительных чисел R и комплексных чисел C. В этом разделе введем аксиоматически линейные пространства.

Пусть дано любое числовое поле и все скаляры являются его элементами 11.

Определение. Линейным пространством над числовым полем, например R, называется множество L элементов, удовлетворяющее аксиомам:

1. Для любой пары ,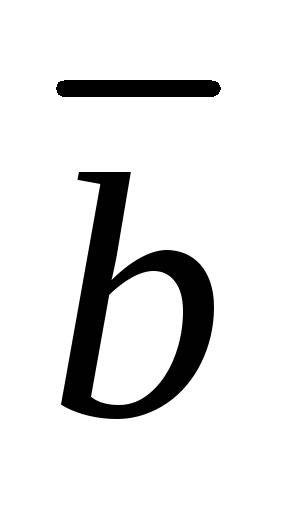элементов изL всегда найдется элемент , называемый суммой элементови, что выполняется

1. (коммутативность);

2. (ассоциативность);

3. существует нейтральный элемент , называемый начальным, такой, что;

4. каждому элементу соответствует однозначно определенный элемент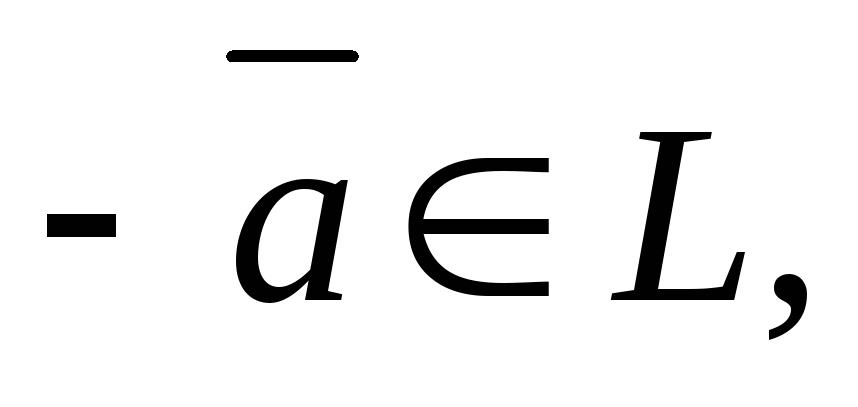такой, что.

2. Для любой пары из ,  и ,,найдется элемент,, называемый произведением и или и соответственно, такой, что

5. (ассоциативность умножения на скаляры);

6. .

7. –умножение на скаляры дис-трибутивно (сочетательно) относительно сложения;

8. –умножение на элементы дис-трибутивно относительно сложения скаляров.

Отношения между линейным пространством L и полем скаляров выражают словами: линейное пространство L над полем скаляров.

В дальнейшем под полем скаляров будем понимать основное поле R действительных чисел, а имея дело с линейными пространствами в обозначениях и геометрической интерпретации, будем использовать векторные обозначения, что и было сделано в аксиомах.

Вектор (лат. vector – скользящий) – в геометрическом пространстве определяется как отрезок прямой, имеющий направление; задается упорядоченно: начало вектора (точка A) и конец (точка B). Для обозначения такого вектора используются а) пара букв или, а также одна букваилиa (полужирный шрифт), б) на рисунках как направленный отрезок прямой. Таким образом, векторные обозначения и геометрические векторы – суть обозначения элементов линейного пространства.

Рассматривают геометрические векторные пространства трех видов векторов: связанные, скользящие и свободные. В пространстве свободных векторов достаточно иметь одинаковые направления; скользящие векторы лежат на одной прямой; связанные векторы имеют общее начало. Длина для всех видов векторов определяется его модулем  . Из условия упорядоченности обозначений векторпротивоположен вектору. Вектор, у которого начало совпадает с концом, например, называется нуль-вектором,, то есть обозначение совпадает с числом 0; ему приписывают любое направление. Вектор, длина которого, называется единичным, помимо этого свойства, он выполняет функции масштаба.

Векторы называются коллинеарными, если они лежат в одной или в параллельных прямых, и компланарными, если лежат в одной или параллельных плоскостях.

Зададим вектор (свободный) аксиоматически. Определим векторное пространство как понятие, обобщающее понятие совокупности всех векторов обычного трехмерного пространства. Элементы числового поля будем называть по-прежнему скалярами.

Определение. Векторным пространством над скалярным полем P называется множество L векторов, в котором определена операция сложения векторов и операция умножения векторов на скаляры из основного поля P, задаваемых аксиомами:

1. Сложение. ,, называемый суммой векторови, что

1. ;

2. ;

3. существует нулевой вектор такой, что;

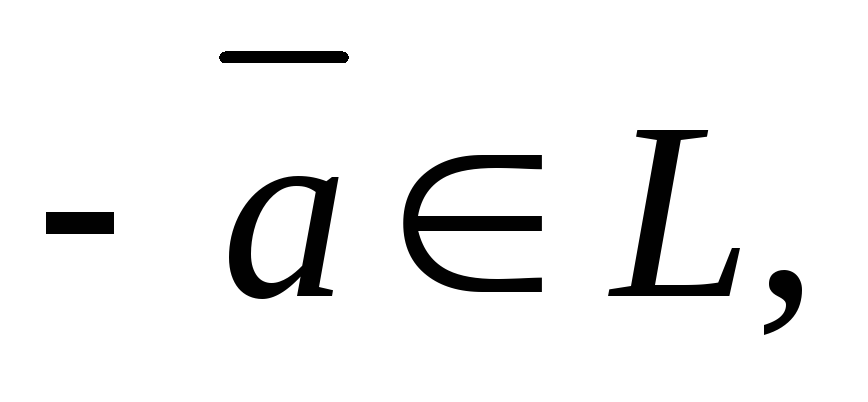4. для вектора найдется единственный противоположный вектортакой, что;

2. Умножение. ,  вектор , называемый произведением скаляра и вектора , что

5. ;

6. ;

3. Умножение дистрибутивно относительно

7. сложения векторов, ;

8. сложения скаляров, .

Из аксиом вытекают важные свойства векторов L ():

1. ; то есть умножение нуль–вектора на скаляр дает число 0;

2. ; умножение числа 0 на вектор дает также число 0;

3. , то есть чтобы получить вектор, противоположный заданному, достаточно умножить его на 1.

Аксиомы 1) – 4) образуют абелеву группу, а аксиомы 5) – 8) отражают тот факт, что умножение элементов на скаляры является линейной функцией (оператором, преобразованием) элементов из L. Это подтверждает не только внешнее сходство аксиом поля и векторного пространства, но и их внутреннюю связь, другими словами, понятия линейное пространство и векторное пространство – изоморфны.

Пример III.1. Рассмотрим множество векторов на плоскости. Покажем, что оно образует линейное пространство L² над полем чисел R. Достаточно проверить выполнение аксиом 1) – 8). Проверку осуществим, используя геометрические образы. Исходя из определения свободных векторов ,, совместим параллельным переносом конец векторас началом вектора, а затем – начало векторас концом вектора. Полученный векторназовем суммой векторови(рис.III.1), то есть .

Положим , тогда, аналогично, тогда(рис.III.1).

А. Сложение. Если векторы неколлинеарные, то по «правилу треугольников» сложения векторов, имеем

1) .

Рис. III.1

Для коллинеарных векторов это очевидно, так как ADB вырождается в отрезок прямой.

2) или.

Тот факт, что векторы параллелограмма попарно равны, не является принципиальным. Для общего случая, можно рассмотреть любой четырехугольник на плоскости.

3) Очевидно, если обозначить ;

4) Следует из доказательства аксиомы 2.

B. Умножение. Пусть лежит на прямой (рис.III.2).

5) ;

Рис. III.2

6) положим , а(рис.2), тогдаили.

C. Дистрибутивность.

7) Следует из свойств пропорциональности отрезков (рис. III.3). В самом деле, . Пусть, тогда

, , .

Рис. III.3

8) Следует из рис. III.2 и правил сложения векторов, если положить ,,, тогда.

Тем самым выполнение аксиом показано геометрически.

Пример III.2. Пусть R² множество всех упорядоченных пар действительных чисел и ,, где. Положим по определению

1) ;

2) ;

3) ;

4) ,

где .

Аксиомы групп A, B, C, очевидно, выполняются, следовательно, R² – двумерное действительное линейное пространство, в котором задана система координат.

Пример III.3. Если в примере 2 вместо пар рассматривать действительные числа, то множество R есть линейное пространство над самим собой, геометрически это числовая ось.

То же самое справедливо для любого другого скалярного поля.

Пример III.4. Пусть  – множество полиномов (многочленов) переменной x с действительными коэффициентами. Под сложением полиномов будем понимать обычное их сложение по правилу приведения подобных членов, а умножение на скаляр – обычное умножение полинома на действительное число. Нейтральный элемент – полином, все коэффициенты которого равны 0. Множество полиномов с действительными коэффициентами будет действительным линейным пространством.

Пример III.5. Определим на множестве действительных чисел R сложение действительных чисел и их умножение на скаляр являющегося рациональным числом, тогда множество R будет рациональным действительным линейным пространством.