§4. Закон больших чисел

Отдельные явления, которые мы наблюдаем в природе и о6щественной жизни, часто проявляются как случайные. Причиной этого является влияние многих побочных факторов, вообще говоря, не связанных с существом данного явления. Учесть суммарное действие этих факторов невозможно, и потому по единичному наблюдению случайного явления ничего нельзя сказать о его закономерностях. Однако давно было замечено, что при большом числе наблюдений случайного явления средние значения его числовых показателей подвергаются лишь незначительным колебаниям, т. е. как бы утрачивают характер случайного. Поэтому естественно считать, что именно средние значения показателей являются истинными характеристиками случайных явлений. Например, для определения веса или длины какого-нибудь предмета обычно производят несколько измерений, и за искомый результат принимают среднее арифметическое значение этих измерений. Теоретически этот метод обосновывается с помощью так называемого закона больших чисел, который представляет собой набор следующих утверждений. Неравенство Маркова. Если случайная величшна Х принимает неотрицательные значения и имеет математическое ожидание М(Х), то для любого положительного числа А выполняется неравенство

(67)

Здесь слева вероятность того, что случайная величина Х принимает значения не меньше, чем число А.

Пример 28. Среднее число дождливых дней в году в г. Кисловодске равно 60. Оценить вероятность того, что в течение года в этом городе будет: а) не менее 100 дождливых дней; б) менее 120 дождливых дней. Решение. Пусть Х - число дождливых дней в году в г. Кисловодске. Тогда Х неотрицательная случайная величина, ее значения колеблются вокруг 60 и, следовательно, 60 можно взять за ее математическое ожидание: М(Х)= 60. а). Применяется неравенство Маркова: 6). Событие Х < 120 является противоположным событию Х  120, поэтому Р(Х <120) = 1 — Согласно неравенству Маркова, Тогда Р(Х <120)  10,5 = 0,5. Ответ: а) Р(Х <120)  0,6; 6) Р(Х <120)  0,5. Неравенство Чебышева. Если случайная величина Х имеет дисперсию D(Х), то для любого положительного числа выполняется неравенство:

Здесь слева вероятность того, что значения случайной величиям Х отклоняются от М(Х) не более чем на по абсолютной величине. Пример 29. Средняя урожайность люпина составляет 250 ц. с га. Оценить вероятность того, что урожайность люпина с наудачу выбранного гектара будет в границах от 225 до 275 включительно, если известно, что среднее квадратическое отклонение урожайности равно 10 ц. Найти приближенно эту вероятность, по формуле (66).

Решение. Пусть Х  урожайность люпина. Тогда Х имеет дисперсию D(X) = 10² = 100. Математическое ожидание равно средней урожайности: М(Х) = 250. Границы 225 и 275 симметричны относительно 250, поэтому можно применить неравенства Чебышева. Очевидно, что 225 Х  275  25, поэтому, =

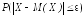
Урожайность люпина зависит от многих независимых случайных факторов, по теореме Ляпунова можно считать, что Х имеет распределение близкое к нормальному закону, поэтому можно применить формулу (66): 2·Ф(2,5) = 0,9976. Получили разные ответы, но противоречия нет, ибо первый ответ 0,84 - это нижняя оценка искомой вероятности, второй ответ 0,9976  это более точная приближенная оценка значения этой же вероятности. Теорема Чебышева. Пусть дана последовательность случайных величин Х₁, Х₂ ,..., Х_n ,..., и их дисперсии ограничены одним и тем же числом С. Пусть `Х<sub>n</sub> обозначает среднее арифметическое первых п случайных величин и `М_n - среднее арифметическое их математических ожиданий: . Тогда имеет место неравенство для любого положительного числа . (Здесь величина справа стремится к 1 при ).

Значение теоремы Чебышева. В практических исследованиях очень важно знать, какие случайные события могут произойти или не произойти в данный момент. В таких случаях определяют вероятность этого события и руководствуются следующим принципом. Принцип практической уверенности: Если вероятность события очень мала (например, меньше 0,03), то при однократном испытании можно быть уверенным в том, что это событие не произойдет, и в практической деятельности можно считать это событие невозможным. Например, в каждой лотерее вероятность выигрыша по одному балету не более чем 0.01. Поэтому выиграть по одному билету практически невозможно.

Пусть наблюдается достаточно большое число случайных величин Х₁, Х₂ ,..., Х_n ,.... Каждая Х_n принимает значения вокруг своего математического ожидания М(Х_n), и эти значения невозможно предсказать. Часто оказывается, что отклонения Х_n от М(Х_n) ограничены, например, если все Х_n - результаты измерения одного и того же объекта. Тогда можно применять теорему Чебышева. Пусть взято малое число и рассматривается среднее арифметическое`Х<sub>n</sub> . По теореме Чебышева, при достаточно большом n величина`Х_n принимает свои значения в пределах от `М<sub>n</sub>  до `М_n +  с вероятностью близкой к 1. Значит, вероятность отклонения `Х<sub>n</sub> от `М_п,, на большую величину 6лизка к 0. Поэтому можно считать, что`Х<sub>n</sub> практически не отклоняется от `М_n . Но`М<sub>n</sub> - это постоянная величина, которая может быть заранее вычислена. Таким образом, теорема Чебышева утверждает, что значения средних величин `Х_n (при достаточно большом n) можно рассматривать как функциональные величины, и потому их значения можно предсказывать. Следствие теоремы Чебышева. Если случайные величины Х₁, Х₂ ,..., Х_n ,.. (из теоремы Чебышева) имеют одинаковые математические ожидания, равные а, то для любого положительного числа  вероятность стремится к1 при n . Теорема Бернулли. Пусть производится серия независимых повторных испытаний, в каждом из которых событие А может наступить с вероятностью р. Тогда для любого положительного числа  вероятность

стремится к 1 при n , где относительная частота появления А в испытаниях. Эта теорема утверждает, что при достаточно большом числе испытаний ве­роятность события А практически равна его относительной частоте. Следствие теоремы Ляпунова. Если случайная величина Х является сум­мой достаточно большого числа независимых случайных величия, влияние ко­торых на Х незначительное, то распределение Х близко к нормальному за­кону. В практических исследованиях очень часто рассматриваются случай­ные величины, удовлетворяющие требованиям теоремы Ляпунова. И поэтому ис­следователи могут предполагать, что такие случайные величины имеют нор­мальный закон распределения. Этот обстоятельство широко используется при разработке многочисленных методов математической и общей стати­стики.