
Радиотехнические цепи и сигналы
.pdf
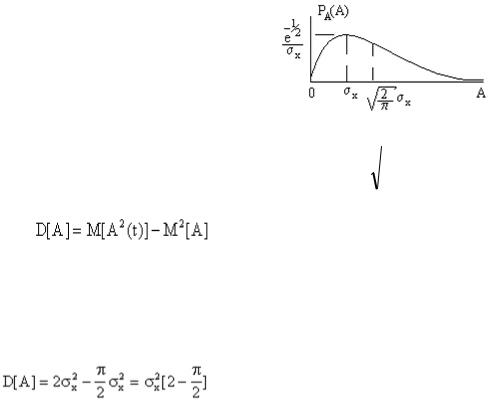
dAS в интервале dAS и равна вероятности пребывания вектора A(t) в элементарной площадке dAdθ .
P(Ac;As)= f(Ac) f(As)dAdAc s – вероятность того, что вектор A(t)
пребывает |
в элементарном |
прямоугольнике. В |
полярных координатах: |
||||||||||||
P(A,θ) = f (A,θ)dAdθ . |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
− |
A2 |
|
|
|
Тогда f (A,θ) = |
f (A ) f (A ) A= |
A |
2σ2 |
|
|
||||||||||
|
|
|
|||||||||||||
|
e |
x |
|
|
|||||||||||
2πσx2 |
|
|
|||||||||||||
|
|
|
|
|
c |
|
s |
|
|
|
|
|
|||
Плотность |
|
распределения |
|
|
огибающей |
(амплитуды): |
|||||||||
|
π |
|
|
A |
|
− A 2 |
|
|
|
|
|
|
|||
f (A)= |
f(A,θ)dθ = |
|
e |
2σ |
2 |
|
|
|
|
|
|
|
|||
|
∫ |
|
|
|
X - |
закон |
|
Рэлея, |
т.к. |
f (A,θ) = f (A) f (θ), |
|||||
2 |
|
|
|||||||||||||
A |
−π |
|
σ X |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||||
то f (θ )= |
1 |
-равномерная плотность распределения. |
|
|
|||||||||||
2π |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вывод: если случайный процесс распределен по нормальному закону, то его огибающая распределена по рэлеевскому закону, а фаза по равномерному закону.
|
|
|
|
|
|
M [A] |
∞ |
|
|
(A)dA = |
π |
|
|
|||
Математическое ожидание: |
|
= ∫ AfA |
σ X |
|||||||||||||
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Дисперсия: |
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
||
|
|
∞ |
|
∞ |
1 |
|
|
− A2 (t) |
|
|
|
|
||||
2 |
|
2 |
3 |
|
|
2σ |
2 |
|
2 |
|
|
|||||
|
|
|
|
|
|
|
|
x |
|
|
|
|||||
где M A |
(t) |
= ∫ |
A |
(t) f (A)dA = ∫ |
|
|
|
A |
(t)e |
|
|
|
dA = 2σx . |
|||
σ |
2 |
|
|
|
||||||||||||
|
|
0 |
|
0 |
x |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
отсюда |
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
Т. е. дисперсия огибающей меньше дисперсии самого случайного процесса.
Вероятность того, что огибающая (амплитуда) превысит некоторый заданный уровень:
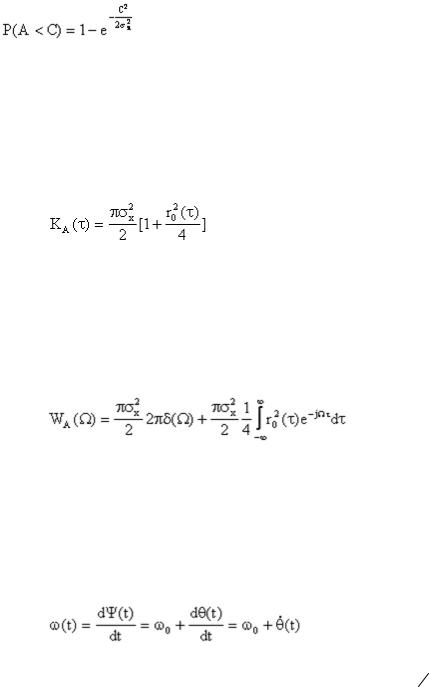
∞ |
|
1 |
∞ |
− |
A2 |
|
|
C 2 |
|
||
P(A f C )= ∫ |
f (A)dA = |
∫ Ae |
2σ X 2 |
dA = e− |
2σ X2 |
||||||
2 |
|
||||||||||
0 |
|
σ |
X |
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Вероятность |
того, что |
|
амплитуда |
будет ниже уровня С: |
|||||||
. |
|
|
|
|
|
|
|
|
|
|
|
Если 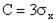 , то
, то 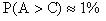 . Поэтому ширина шумовой дорожки, фактически наблюдаемой на экране осциллографа не превышает (5-6)σ X . Для широкополосных процессов ширина дорожки составляет (4-5) σ X .
. Поэтому ширина шумовой дорожки, фактически наблюдаемой на экране осциллографа не превышает (5-6)σ X . Для широкополосных процессов ширина дорожки составляет (4-5) σ X .
Корреляционная функция огибающей определяется по формуле:
где r0(τ)– огибающая нормированной корреляционной функции случайного процесса х(t).
Энергетический спектр огибающей найдем через преобразование
Фурье:
.
Первое слагаемое соответствует постоянной составляющей огибающей, а второе – сплошной части спектра.
Основываясь на выражении 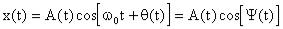 , мгновенную частоту можно записать в форме:
, мгновенную частоту можно записать в форме:
& |
|
|
|
θ |
32 |
−1 |
|
|
Плотность вероятности: f (θ )= |
|
|
+ |
|
|
|
, |
|
2 |
||||||||
|
2 ωэкв 1 |
|
|
|||||
|
|
|
ωэкв |
|
||||
|
|
|
|
|
|
|
|
|
где Δωэкв – эквивалентная ширина спектра узкополосного процесса, определяемая выражением:

ω экв f (θ )
Не удаетсяотобразить связанный рисунок. Возможно, этот файлωбыл перемещен,эквпереименован или удален. Убедитесь,fчто(ссылкаθуказывает&на правильный)файл и верное размещение.
Частота случайного сигнала изменяется в пределах ±2 ωэкв .
Закон распределения похож на нормальный.
Гармонические колебания со случайной амплитудой
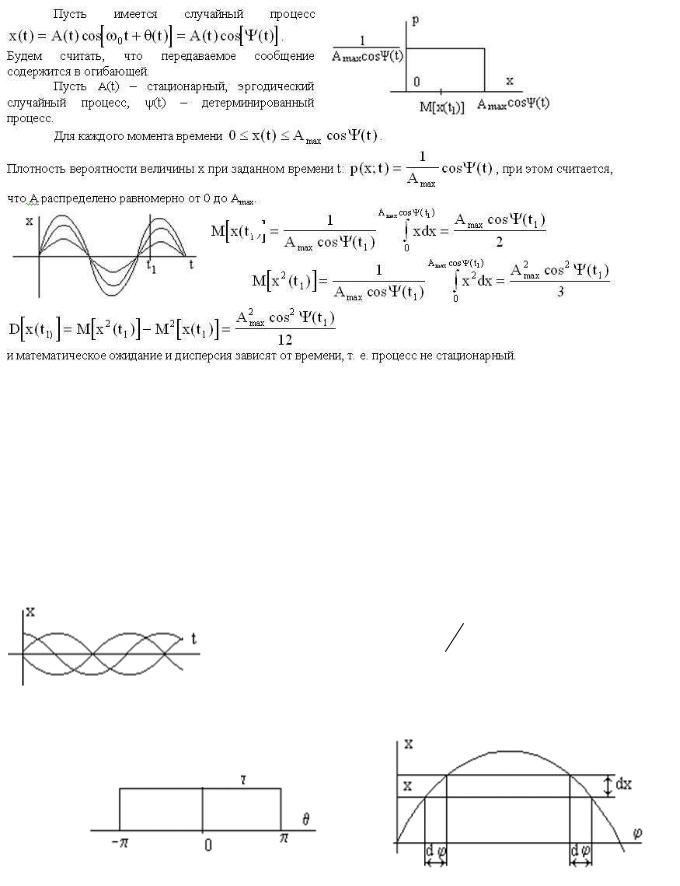
f(x)
Гармонические колебания со случайной фазой
Имеется случайный процесс x(t) = cos[ω0t +θ(t)] . Найдем закон распределения фазы ϕ(t) =ω0t +θk .
Начальная фаза обычно распределена по равномерному закону. f (θ)= 12π .
f (θ)
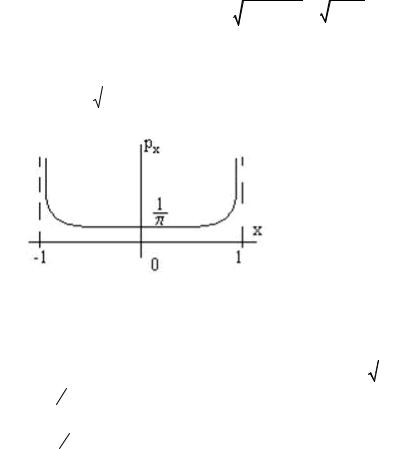
При суммировании нескольких гармонических колебаний (5 -6) со случайной фазой мы получим стационарный случайный процесс близкий к гаусовскому, что соответствует теореме Чебышева о суммировании большого числа гармонических процессов с малыми, близкими по величине амплитудами.
Комплексный случайный процесс
Пусть есть случайный процесс x(t). Подберем ему сопряженный по Гильберту сигнал xˆ(t)
xˆ(t)= 1 ∞∫ x(τ )dτ
π −∞τ − t
•
Тогда комплексный случайный процесс: z(t)=x(t)+ jxˆ(t).
Пусть x(t)= A(t)cos[ω0t +θ (t)], тогда xˆ(t)= A(t)sin[ω0t +θ(t)]. Отсюда комплексный
•
случайный процесс: z(t)= A(t)e jω0t+θ (t )
Спектры сигналов x(t)и xˆ(t) равны: WX (ω)=WXˆ (ω). Отсюда следует что корреляционные
функции одинаковы RX (τ)=Rˆ (τ)= |
1 |
∞ |
(ω)ejωtdω. |
||||
WX |
|||||||
|
|||||||
|
|
|
X |
2π ∫ |
|
||
|
|
|
|
|
−∞ |
|
|
Дисперсии: DX |
= D ˆ = |
1 |
∞WX (ω)dω . |
|
|||
|
|
||||||
|
X |
2π ∫ |
|
|
|
||
|
|
|
−∞ |
|
|
|
|
Предположим, что xKT(t) соответствует x• KT(ω), тогда xˆKT(ω) xKT(ω)ejϕ , где ϕ = −90o . Т.е.

ˆ |
|
• |
|
|
− j X KT (ω)приω f 0 |
||||
XKT |
(ω)= |
|
|
|
• |
|
|
||
|
|
+ j XKT (ω)приω |
p |
0 |
|
|
|
||
|
|
• |
(ω)+ j[− jXKT (ω)]= 2XKT (ω), а при ωp0 |
Отсюда следует, что при ω f 0 |
ZKT (t)= XKT |
||
• |
(ω)]= 0 |
|
|
ZKT (ω)= j[XKT |
|
|
|
Вывод: спектр комплексного случайного сигнала отличен от 0 только на положительных частотах.
Спектральная характеристика мощности и корреляционная функция случайного процесса на выходе цепи
|
|
|
|
|
|
|
|
|
|
|
|
|
• |
|
|
Если есть к-ая реализация на интервале XKT(t) |
имеет спектр XKT(ω), то на |
||||||||||||||
выходе цепи спектр сигнала: |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
• |
• |
• |
|
|
|
|
|
|
|
|
|
|
|
|
|
XвыхКТ(ω)= XKT(ω)K(ω) |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
T 2 |
• 2 |
|
∞ |
|
• |
|
2 |
|
• |
|
2 |
|
|
|
|
|
|
|
|
|
|||||||
По теореме Парсеваля: выхKT |
|
∫ |
|
2π ∫ |
|
|
|
|
|
|
|
|
|||
|
|
Э |
= |
|
X выхKT (t)dt = |
1 |
|
|
X KT (ω) |
|
|
|
K(ω) |
|
dω |
|
|
−T 2 |
|
−∞ |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Определим спектральную плотность мощности на входе цепи:
•(ω) 2X вхKT
Wвых |
(ω)= lim |
|
, тогда спектральная плотность мощности на выходе: |
|
|||
|
T→∞ |
T |
|
Wвых(ω)=W(ω)K2(ω). Возведение передаточной функции в квадрат объясняется тем, что она определяет отношение напряжений (токов) на входе и выходе, а W(ω) является спектральной плотностью мощности случайной функции.
Корреляционная функция случайного процесса на выходе цепи по теореме Винера-Хинчина:

R |
|
(τ )= |
1 |
∞W |
|
(ω)e jωt dω = |
1 |
∞W (ω)K 2 |
(ω)e jωt dω |
|
2π |
|
2π |
||||||
|
вых |
|
∫ |
вых |
|
∫ |
|
||
|
|
|
|
|
|
|
|
||
|
|
|
|
−∞ |
|
|
|
−∞ |
|
Корреляционная функция входного сигнала: R(τ )= 1 ∞∫W(ω)ejωτ dω
2π −∞
Корреляционная функция импульсной характеристики:
R (τ )= |
1 |
∞ K2 |
(ω)ejωτ dω |
|
|||
g |
2π ∫ |
|
|
|
|
|
|
|
|
−∞ |
|
Следовательно, произведению спектральных функций W(ω) и K(ω) соответственно свертка функций Rвх (τ ) и Rg (τ ):
∞
Rвых(τ )= ∫R(x)Rg (τ − x)dx. Отсюда зная корреляционные функции Rвх(τ) и
−∞
∞
Rg (τ) можно найти энергетический спектр: Wвых (ω)= ∫Rвых (τ )e− jωt dτ .
−∞
Пусть на входе белый шум (спектральная плотность равнаW0 = const на всех частотах), следовательно: Wвых(ω)=W0K2(ω), тогда:
Rвых (τ )=W0 |
1 |
∞ |
(ω)e jωt dω =W0 Rg |
(τ ) |
|
∫K 2 |
|||||
2π |
|||||
|
|
−∞ |
|
|
Следовательно, если мы знаем вид корреляционной функции импульсной характеристики, то Rвых(τ) имеет такой же вид.
Нормализация случайных процессов в узкополосных линейных цепях
Пусть на входе линейной цепи действует стационарный случайный процесс с распределением, отличным от нормального. Если интервал корреляции этого процесса меньше постоянной времени линейной цепи (т. е. ширина энергетического спектра больше полосы пропускания цепи), то распределение случайного процесса на выходе приближается к нормальному. Эффект нормализации тем выше, чем меньше полоса пропускания цепи.
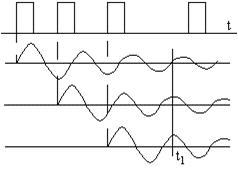
Например. На высокодобротный контур подается случайный процесс, представляющий собой последовательность импульсов со случайным и ненормальным временем появления. На выходе получаем сигнал как сумму свободных колебаний, вызванных предыдущими импульсами и не успевших затухнуть к рассматриваемому моменту времени. Чем уже полоса пропускания цепи, тем большее число соизмеримых по величине и
некоррелированных слагаемых принимает участие в образовании результирующего колебания в момент времени t1. В соответствии с центральной предельной теоремой этого вполне достаточно для того, чтобы процесс приближался к нормальному.
В широкополосных линейных цепях при некоторых условиях может иметь место обратный эффект :распределение процесса на выходе цепи может отличаться от нормального, чем на входе.
Например: На вход дифференцирующего устройства подается совокупность относительно длительных импульсов, имеющих распределение близкое к нормальному. В результате дифференцирования каждый импульс превращается в пару очень коротких импульсов, соответствующих фронтам входного импульса. Число взаимно перекрывающихся импульсов на выходе уменьшится, т.е. распределение приближается к нормальному закону. Это денормализация. Этот эффект не противоречит тому, что в любой линейной цепи гаусовский процесс сохраняет нормальное распределение. Если среднее количество импульсов увеличить до бесконечности в единицу времени(это необходимо для получения строго нормального распределения), то при любом сжатии импульсов, которое можно осуществить в физически реализуемой цепи, процесс будет гаусовским и на выходе цепи.
Преобразование нормального процесса в безынерционных нелинейных цепях
Внелинейных безынерционных элементах основная трудность состоит
внахождении корреляционной функции. Поэтому общих методов анализа преобразования случайный процессов в нелинейных устройствах не существует. Приходится ограничиваться частными задачами, поддающимися решению.

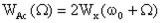 . Из этого выражения
. Из этого выражения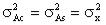
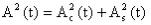 , то среднее значение квадрата огибающей
, то среднее значение квадрата огибающей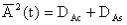 . Так как дисперсии равны, то
. Так как дисперсии равны, то  . Плотности вероятностей определяются как
. Плотности вероятностей определяются как