Радиотехнические цепи и сигналы

Рассмотрим теперь случай неточной настройки контура на несущую частоту модулированного колебания. Несовпадение частот ω0 и ωР приводит к

асимметрии боковых частот на выходе усилителя. Возникновение асимметрии поясняется векторной диаграммой выходных напряжений, представленной на рис На этой диаграмме вектор ОВ изображает несущее колебание, фаза которого запаздывает относительно фазы входной ЭДС (принятой равной нулю) на угол θ0 (так как рис. соответствует положительной расстройке ΔΩ = ω0 −ω р > 0. Амплитуда колебания верхней

боковой частоты (вектор ВС) в данном случае значительно меньше амплитуды колебания нижней боковой частоты (вектор DC2). Длина равнодействующего вектора OF, изображающего результирующее колебание, изменяется по сложному закону, не совпадающему с гармоническим законом изменения огибающей входной ЭДС.

Следует иметь в виду, что для восстановления передаваемого сообщения на выходе радиолинии, работающей с амплитудной модуляцией, применяется амплитудный детектор, представляющий собой нелинейное устройство.

Напряжение на выходе детектора пропорционально огибающей модулированного колебания. Из этого следует, что нарушение симметрии амплитуд и фаз колебаний боковых частот при неточной настройке контура на несущую частоту ω0 приводит к нелинейным искажениям передаваемых сообщений.

Эти искажения проявляются в возникновении новых частот, кратных частоте

• полезной модуляции.

Кроме искажения формы огибающей амплитуд, возникает также паразитная фазовая модуляция колебания, так как при вращении векторов DC1 и DC2 (см. рис. 6.20) непрерывно изменяется фаза θ(t) вектора OF относительно фазы несущего колебания (принятой в качестве исходной). В некоторых случаях это может привести к дополнительным искажениям сигнала. Полученные выше результаты нетрудно распространить на любую колебательную цепь, например на связанные контуры. Если резонансная кривая

такой цепи симметрична относительно несущей частоты ω0 , то правую

ветвь этой кривой можно рассматривать как характеристику коэффициента D.

Прохождение частотно – модулированного колебания через избирательные цепи.

Ранее было показано, что при гармонической АМ передача колебания через контур, точно настроенный на несущую частоту, не сопровождается изменением формы огибающей, имеет место лишь ослабление глубины модуляции. При ЧМ неравномерность амплитудно-частотной и кривизна фазо-частотной характеристик контура оказывают более сложное влияние на параметры выходного колебания. Даже при гармонической модуляции частоты спектр колебания обычно содержит очень большое число пар боковых частот. Нарушение нормальных амплитудных и фазовых соотношений между отдельными парами боковых частот приводит к искажению закона модуляции даже при полной симметрии характеристик цели относительно несущей частоты колебания.

При ЧМ влияние цепи может сказаться:

1)в искажении закона изменения мгновенной частоты и мгновенной фазы колебания;

2)в изменении амплитуды полезного частотного отклонения в зависимости от частоты модуляции •;

3)в возникновении паразитной АМ.

При детектировании колебаний с помощью частотного детектора напряжение на выходе приемника пропорционально изменению мгновенной частоты колебания. Поэтому искажение закона изменения мгновенной частоты в колебательных контурах передатчика и приемника приводит к

нелинейным искажениям сигнала, проявляющимся на выходе детектора в виде добавочных напряжений с частотами, кратными частоте модуляций Ω. Второе из отмеченных выше изменений параметров частотно-модулиро- ванного колебания приводит к неравномерности АЧХ радиолинии с ЧМ и, следовательно, к частотным (линейным) искажениям сигнала. Рассмотрим воздействие ЭДС, частота которой изменяется по закону

ω(t) = ω0 +ω∂ cosΩt

на резонансную колебательную цепь. Амплитуду ЭДС считаем строго постоянной, так что ЭДС можно представить выражением:

e(t) = E0 cos(ω0t + msinΩt) .

Комплексный коэффициент передачи цепи обозначим через:

K(iω) = K(ω)eiϕ(ω) .

Примерный вид модуля K (ω ) и фазы ϕ (ω ) для обычной резонансной цепи изображен на рис. 6.26, а. Так как перед ϕ(ω) выбран знак плюс, то фазовая характеристика ϕ(ω) имеет отрицательный наклон в полосе прозрачности цепи. Частотный спектр и график изменения мгновенной частоты ω(t)

входной ЭДС показаны на рис. б и в. Колебательные цепи обычно настраиваются на среднюю частоту модулированного колебания, поэтому рис. и дальнейшее рассмотрение относятся к случаю ωр =ω0.

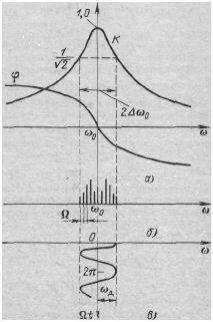
Рис. Передаточная функция цепи (а), спектр ЧМ колебания (б) и график мгновенной частоты (в) этого колебания.

Для нахождения колебания на выходе цепи в принципе можно воспользоваться тем же методом, что и в случае АМ. При этом необходимо учесть изменение амплитуд и фаз для каждой из пар боковых частот ЭДС в соответствии с кривыми K(ω) и ϕ(ω). Однако подобный вполне точный метод пригоден лишь при очень малых индексах модуляции, т. е. если состав спектра ЧМ колебания мало отличается от состава спектра АМ колебания. В практике чаще всего приходится встречаться с модуляцией, характеризующейся столь большим числом спектральных составляющих в используемой полосе частот, что применение спектрального метода

сопряжено с большими, иногда непреодолимыми трудностями вычисления. В таких случаях приходится прибегать к приближенным методам, позволяющим, хотя и не вполне точно, находить колебание на выходе цепи по заданному закону изменения мгновенной частоты ЭДС на входе и по заданным ФЧХ цепи без разложения ЭДС в спектр.

Эти методы, называемые методами мгновенной частоты, основаны на допущении медленности изменения частоты. Частота модуляции считается настолько малой, что амплитуду и фазу колебания на выходе цепи в каждый момент времени можно без большой погрешности определить по частотной и фазовой характеристикам цепи так же, как и в стационарном режиме. Таким образом, принимается, что установление стационарных колебаний на выходе происходит почти одновременно с изменением частоты на входе цепи.

Эти предпосылки тем ближе к истине, чем больше период модуляции 2π . и

Ω

чем меньше постоянная времени цепи τк . Так как последняя обратно пропорциональна полосе пропускания цепи 2 ω0 , то одним из условий применимости метода мгновенной частоты является неравенство Ω ω0 <<1. При одной и той же частоте • скорость изменения мгновенной частоты входной ЭДС зависит от амплитуды частотного отклонения ωд , поэтому соблюдения только этого неравенства еще недостаточно. Должны быть наложены ограничения и на отношение ωд ω0 .

Прохождение фазоманипулированного колебания через резонансную цепь.

Наряду с непрерывной фазовой модуляцией в радиотехнике находит применение фазовая манипуляция, заключающаяся в скачкообразном изменении фазы высокочастотного колебания на 180° в определенные моменты времени (рис. а). Амплитуда и частота колебания поддерживаются при этом неизменными. На (рис. Б) фазы 0 и π чередуются периодически; при передаче реальных сигналов закон чередования может быть более сложным. Рассмотрим явления в резонансных цепях, возникающие в моменты скачкообразного изменения фазы входного сигнала. При этом будем считать, что

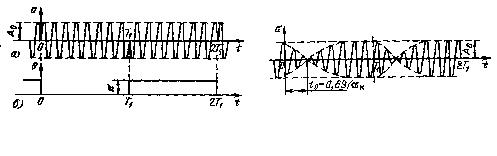
больше добротность контура), тем больше t0 т. е. тем протяженнее процесс установления колебания с новой фазой.

В более сложных колебательных цепях, а также при наличии расстройки между частотами ω0 и ωр картина несколько усложняется: помимо

возникновения паразитного изменения огибающей нарушается и характер изменения фазы. Вместо скачкообразного изменения получается плавный переход фазы от первоначального значения к новому. При этом способ определения Структуры выходного сигнала остается прежним, в

выражении для sвых будут представлять собой колебания с

несовпадающими частотами. Вычислив модуль и аргумент суммарного колебания, нетрудно найти огибающую и фазу выходного сигнала.

Нелинейные элементы.

Радиотехнические преобразования проводят на нелинейных элементах либо на элементах с переменными параметрами. В качестве нелинейных элементов используются резистивные и реактивные элементы, полупроводники и лампы, имеющие нелинейную характеристику.

Параметры нелинейных элементов определяются:

1)Средней крутизной вольтамперной характеристики при сильном сигнале;

2)Крутизной в рассматриваемой рабочей точке U0 при слабом сигнале

Аппроксимация нелинейных характеристик.

Замена истинной характеристики приближенной, называется

аппроксимацией.

1) Аппроксимация степенным полиномом i(u)=i(u0) + a(u- u0) + a2(u- u0)2 + …

a1,a2 ,a3 - зависит от u0, т.е. от положения рабочей точки.

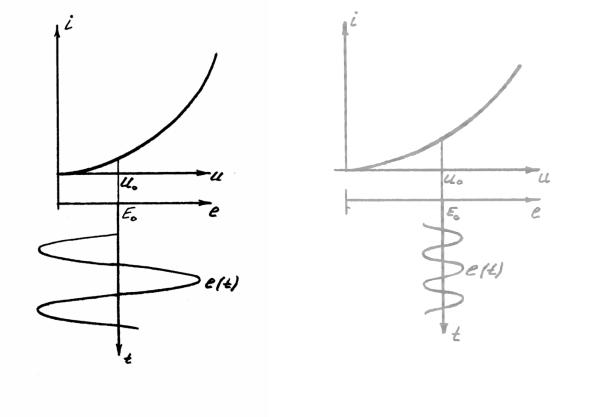
а) рабочая точка находится на начальном участке характеристики, имеющем вид квадратичной параболы. Подводимое напряжение e

накладывается на E0 = u0 и не выходит за начало характеристики u0 .

i(u0 +e)=i(u0 )+a1e+a2e

при e=u1-u0 , то i=0, т.е.:

б) рабочая точка является точкой перегиба характеристики, в ней все производные четные и равны 0.

ах ах

i(u) = i(u0 ) + a1 (u − u0 ) + a3 (u − u0 )3 + ...;

или

i(u) = i(u0 ) + a1e + a3 e3 + ...;

U max − напряжение насыщения

в т. u0 = Umax

в) рабочая точка находится на нижнем сгибе характеристики. Для описания требуется полином пятой и выше степени, анализ неэффективен.

2)кусочно-линейная аппроксимация:

Нелинейное резонансное усиление.

Рассмотрим существенно нелинейный режим. Рабочая точка сдвигается влево. Используем кусочно-импульсную линейную аппроксимацию. При гармоническом возбуждении ток i(t) приобретает форму:

cos θ = U1 − U 0 , где θ -угол отсечки

E

Im = a1 [E − (U1 −U 0 )]= a1 E(1− cosθ )

i(t)= im' (cosωt − cos a), где −θ p ωt p θ

Im' -амплитуда импульса, при θ =90o

Т.е. Im соответствует ωt = 0, то Im = i(0)= Im' (1−cosθ), т.е.