
Радиотехнические цепи и сигналы
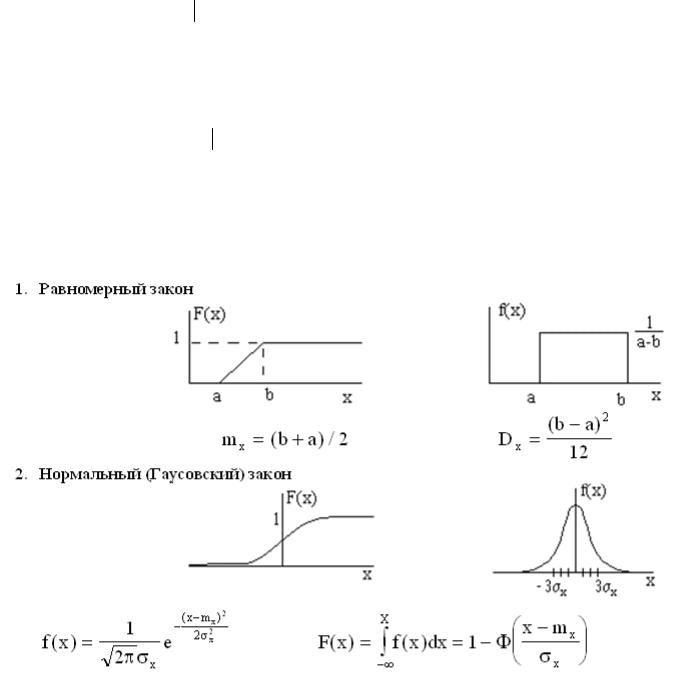
.pdf

1.Классификация случайных сигналов. 1.1. Случайные процессы.
Случайный процесс (СП) – совокупность функций времени, подчиняющихся некоторой, общей для них, статистической закономерности. Различают непрерывные, дискретные, квантованные и цифровые СП. Случайные процессы могут быть стационарными и нестационарными, эргодическими и неэргодическими, марковскими и немарковскими.
Реализацией СП называется одна из функций, составляющих совокупность СП, полученная на ограниченном отрезке времени.
Главной статистической характеристикой СП является интегральный закон распределения F(x): F(x)=P(X<x) – вероятность того, что значение случайного процесса X меньше заданного значения x.
Основные свойства F(x):
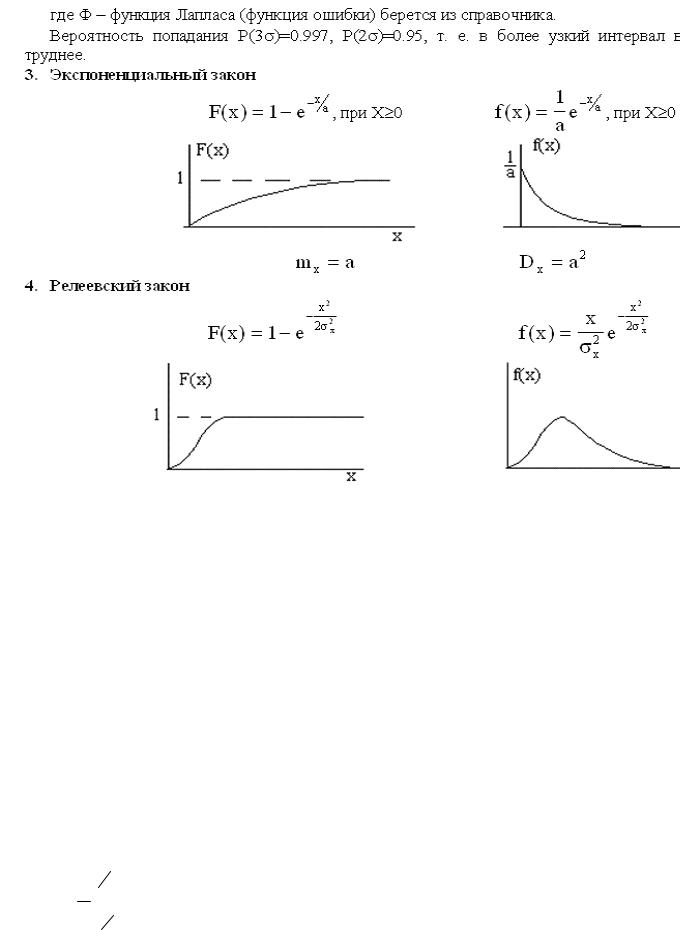
1)F(x2)>F(x1), при x2 > x1 , т.е. F(x) – неубывающая функция
2)F(−∞)=0,F(∞)=1
3)F(x) ≥ 0
Спектральная плотность вероятности
f (x) = F′(x)
Свойства спектральной плотности: 1) f (−∞) =0, f (+∞) =0
∞
∫ f (x)dx =1
2)−∞
3)f (x)≥0

Вероятность попадания в заданный интервал [a, b]
P(a,b)=F(x=b)−F(x=a)
2.Основные параметры случайных процессов.
b
Pt (a ≤ x ≤b) = ∫ f (x(t))dx - вероятность попадания в заданный интервал [a,b], в
a
момент времени t.
∞
mx(t)=M[x(t)]= ∫ x f (x(t))dx - математическое ожидание.
−∞
Dx(t)=M{[x(t)−mx(t)]2} - дисперсия. Характеризует мощность случайного сигнала.
σx(t) =
 Dx(t) - среднеквадратическое отклонение. Характеризует отклонение от математического ожидания случайного процесса.
Dx(t) - среднеквадратическое отклонение. Характеризует отклонение от математического ожидания случайного процесса.
Индекс t для этих параметров означает, что они соответствуют случайному процессу в заданный момент времени t .
Ковариационная функция
∞ ∞
Kx (t1,t2 ) = M [x(t1) x(t2)]= ∫ ∫ f (x1, x2 t1,t2 )dx1dx2
−∞ −∞
Корреляционная функция
Rx(t1,t2) = M[(x(t1)−mx(t1)) (x(t2)−mx(t2))]
Корреляционная и ковариационные функции устанавливают связь между процессами в различные моменты времени.
Если процессы X и Y некоррелированы, то их взаимно корреляционная функция RXY (τ ) = 0 .
Если процессы независимы, то двумерный закон распределения f (x, y) = f (x) f (y).
Независимые процессы всегда некоррелированы.
Зависимые процессы могут быть некоррелированными. Например:
y(t) = A cos ω t, x(t) = A sin ωt, Rxy (τ ) = 0.
Связь значений процесса между собой в различные моменты времени устанавливает автокорреляционная ( или автоковариационная) функция:
∞
Rx (τ) = ∫ x(t1) x(t2) f (x1,x2 τ)dx.
−∞
Связь значений двух процессов в различные моменты времени устанавливает взаимная корреляционная функция:
∞ ∞
Rxy (τ ) = ∫ ∫ x(t1)y(t2 ) f (x, y τ )dxdy .
−∞ −∞
Одномерные законы распределения
Для стационарного процесса
∞
mX = M [x]= ∫ f (x)dx
−∞
DX = M[(x−mX )2 ]= M[x2 ]−mX2
KX (τ )= M[x(t) x(t +τ )]
RX (τ)= M[(x(t)−mX ) (x(t +τ)−mX )]= KX (τ)−mX2
DX = KX (0)−mX2 = RX (0)=σX2
Для эргодического процесса
T
x(t)= lim 1 ∫2x(t)dt
T →∞ T −T 2

K (τ )= lim |
1 |
T 2x(t) x(t +τ )dt |
||
T |
||||
X |
∫ |
|
||
|
|
|
||
|
|
−T |
2 |
|
|
|
|
||
RX (τ )= KX (τ )−(x(t))2
DX = KX (0)−(x(t))2
τX =
 DX
DX
Основные положения ковариационной теории
∞ |
∞ |
Rx1,x2 = ∫ (x1 − mx )(x2 − mx ) f (x)dx = ∫ ((x(t1) − mx )((x(t2 ) − mx ) f (x)dx -
−∞ |
−∞ |
корреляционная функция, характеризующая взаимодействие случайных процессов x1(f ) и x2(f ) между собой в моменты времени t1 и t2 . Чем меньше
значения |
RX X |
, тем, быстрее меняется процесс. |
|
|
1 |
2 |
|
|
|
|
∞ ∞ |
K(x1(t1), x2 (t2 )) = M(x1(t1), x2 (t2 )) = ∫ ∫ x1x2 f (x1,t1, x2 ,t2 )dx1dx2 - |
|||
|
|
|
−∞ −∞ |
ковариационная функция, |
|||
где f (x1,t1, x2,t2 ) - плотность вероятности распределения в моменты времени
t1 и t2 .
При τ = 0, RXX =σX2 , RYY =σY2
RXY (0)= RYX (0),т.е.
DS = RS (0)= DX + DY + 2RXY (0)
Если DS =DX +DY , X (t ) uY (t)-некоррелированный, аддитивный случайный процесс.
Пусть имеется x(f ) и y(f )= kx(t −τ )
RXX (t)= Rx (t)
RXY (τ )= x(t) y(t +τ )= kx(f ) x(t −τ −T)= kRX (τ −T) RYX (τ )= y(t) x(t +τ )= kx(τ −T) x(t +τ )= kRX (τ +T)

RYY (τ )= RY (t)= y(t) y(t +τ)= k2x(t +τ ) (t −T +τ )= k2RX (τ )
|
R X (τ )kR X (τ − t ) |
|
|||
R (τ )= |
|
|
|
|
|
|
2 |
R X |
|
||
kR X (τ + t )k |
|
(τ ) |
|||
RS (τ)= RX (τ)+kRX (τ −T)+kRX (τ +T)+k2RX (τ)
При τ → 0
DS = DX + kRX (−T)+ kRX (T)+ k2DX = (1+ k2 )DX + 2kRX (T)= DX [1+ k2 + 2krX (T)]
Где rX ffτk rX (T)≈0 Если x и y независимы, то
DS = DX + DY
Взаимная корреляционная функция
RXY (τ)= M[x(t) y(t +τ)]
RYX (τ )= M[y(t) x(t +τ )]
Для эргодического процесса,
|
(τ ) = |
|
|
|
1 |
|
T 2 x(t ) y (t + τ )dt |
|||||
R XY |
x(t ) y(t + τ ) = lim |
|||||||||||
T |
||||||||||||
|
|
|
|
|
|
|
∫ |
|
||||
|
|
|
|
|
|
|
|
|
−T |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
1 |
|
T 2 |
||||
|
= |
|
|
|
|
∫ y (t ) x (t + τ )dt |
||||||
R YX |
y (t ) x (t + τ ) = lim |
|
|
|||||||||
|
T |
|
|
|||||||||
|
|
|
|
|
|
|
|
− T |
2 |
|||
|
|
|
|
|
|
|
|
|
|
|
||
Сдвиг на σ одной из функций x(t ); y(t )можно заменить не обратный сдвиг другой функции
RXY (τ )= x(t) y(t +τ )= x(t −τ ) y(t)
RYX (τ )= y(t) x(t +τ )= y(t −τ ) x(t)
RYX (τ )= RYX (−τ ); RYX (τ )= RXY (−τ ), то это не условие четности функции
RYY (τ )RXY (τ ) (τ)RYX (τ )RYY (τ ) = R
RC (τ)= S(t) S(t +τ)= x(t)+ y(t)+ x(t) y(t +τ)+ y(t) x(t +τ)+ y(t) y(t +τ)=
RXX (τ )+ RXY (τ )+ RYX (τ )+ RYY (τ )
Корреляционная функция

|
2 |
|
1 |
∞ |
|
X Ω (ω ) |
|
2 |
|
||
|
|
|
|
|
|||||||
|
= |
∫ |
|
dω |
|||||||
xKT |
|
|
|
|
|
|
|
||||
2π |
|
|
T |
||||||||
|
|
|
|
−∞ |
|
|
|
|
|
|
|
При увеличении Т энергия возрастает, но отношение ЭКТ / Т стремится к некоторому пределу:
|
2 |
|
1 |
∞ |
|
|
X Ω (ω ) |
|
2 |
|
|
|
|
|
|
||||||
|
= |
∫ |
|
|
||||||
xKT |
|
lim |
|
|
|
|
dω |
|||
2π |
|
|
|
|
||||||
|
|
|
− ∞ T → ∞ |
T |
||||||
Отсюда:
|
|
X Ω (ω ) |
|
2 |
|
|
|
|
|
|
|||
lim |
|
|
|
|
= WX (ω ) |
–– спектральная плотность мощности. Это |
|
|
|
|
|||
|
|
T |
|
|||
предел спектральной плотности усеченной реализации отделенной на интервале времени Т.
Выражение справедливо для эргодического процесса. |
|
|
|
|||||||||
При T→∞ и усреднении по одной реализации: |
|
2 |
(t) = |
1 |
∞ |
(ω)dω . |
||||||
x |
|
∫ Wx |
||||||||||
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
2π −∞ |
|
|
|
|
|
|
|
1 |
∞ |
|
|
|
|
|
|
|
|
(t)=0, то x2(t)=Dx Dx = |
|
|
|
|
|
|
||||
Если |
x |
|
∫ Wx(ω)dω. |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
||||||
|
|
|
|
|
2π −∞ |
|
|
|
|
|
|
|
Теорема Винера – Хинчина
Чем больше время корреляции τк , тем меньше полоса частот спектра
сигнала и наоборот. Существует определенная их взаимосвязь, определяемая теоремой Винера - Хинчина.
Это есть соотношение между энергетическим спектром и корреляционной функцией случайного процесса
∞
Wx (ω) = ∫ Kx (τ)e− jωτ dτ
−∞

Kx (τ) = 21π ∞∫Wx (ω)ejωτ dω
−∞
Это прямое и обратное преобразование Фурье соответственно.
При x = 0 :
∞
Wx (ω) = ∫ Rx (τ)e− jωτ dτ
−∞
Rx (τ) = 21π ∞∫Wx (ω)ejωτ dω
−∞
Узкополосный случайный процесс
Узкополосный процесс – это процесс, у которого отношение
эффективной ширины спектра к средней частоте ΔΩ pp 1.
ω0
Реализация случайного процесса: 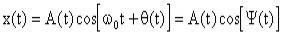 , где A(t) и θ(t) случайные величины.
, где A(t) и θ(t) случайные величины.
Огибающая этого случайного процесса A(t)=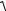
 x2(t)+xˆ2(t), где xˆ2 – сопряженный по Гильберту сигнал.
x2(t)+xˆ2(t), где xˆ2 – сопряженный по Гильберту сигнал.
Будем считать, что x(t) случайный стационарный эргодический процесс.
Представим сигнал в виде квадратурных составляющих:
Отсюда: 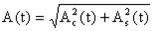 ,
,
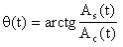 .
.
Нам известна плотность распределения сигнала. Найдем плотность распределения
огибающей fA(A) и фазы fθ (θ) узкополосного процесса.
