Радиотехнические цепи и сигналы

Угловая модуляция.

Для простого гармонического колебания:

a (t ) = A0 cos( ω 0t + θ 0 ) = A0 cos ψ (t)

набег фазы за какой-либо конечный промежуток времени от t = t1 до t = t2 равен

ψ (t1 ) −ψ (t2 ) = (ω 0t2 + θ 0 ) − (ω 0t1 + θ 0 ) = ω 0 (t2 − t1 )

Отсюда видно, что при постоянной угловой частоте набег фазы за какой-либо промежуток времени пропорционален длительности этого промежутка. С другой стороны, если известно, что набег фазы за время t2 – t1 равен

ψ(t2 ) −ψ (t1) , угловую частоту можно определить как отношение

ω0 = (ψ (t2 ) −ψ (t1)) /(t2 + t1) , если, конечно, имеется уверенность, что в

течение рассматриваемого промежутка времени частота сохраняла постоянное значение. Можно показать, что угловая частота есть не что иное, как скорость изменения фазы колебания.

Переходя к сложному колебанию, частота которого может изменяться во времени, выражения необходимо заменить интегральным и дифференциальным соотношениями

ψ (t2 ) −ψ (t1) = t2∫ ω (t)dt

t1

ω (t) = dψ (t) dt

В этих выражениях ω (t) = 2πf (t) — мгновенная угловая частота колебания; f(t) — мгновенная частота.

Полную фазу высокочастотного колебания в момент t можно определить как:

ψ (t) = t∫ω (t)dt +θ0 ,

0

где первое слагаемое в правой части определяет набег фазы за время от начала отсчета до рассматриваемся момента времени, θ0 начальная фаза

колебания.

При таком подходе фазу следует заменить на соотношение

ψ (t) =ω0t +θ (t) +θ0 .

Итак, общее выражение для высокочастотного колебания, амплитуда которого постоянна, а аргумент модулирован, можно представить в форме:

a(t) = A0 cos( ω 0t +θ (t) +θ 0 )

Соотношения, устанавливающие связь между изменениями частоты и фазы, указывают на общность двух разновидностей угловой модуляции — частотной и фазовой.

Поясним эти соотношения на примере простейшей гармонической ЧМ, когда мгновенная частота колебания определяется выражением

ω (t) = ω0 + ωд cos Ωt

где ωд = 2πfд представляет собой амплитуду частотного отклонения. Для

краткости ωд в дальнейшем будем называть девиацией частоты или просто девиацией. Через ω0 и Ω, как и при АМ, обозначены несущая и модулирующая частоты.

Составим выражение для мгновенного значения колебания (тока или напряжения), частота которого изменяется, а амплитуда постоянна.

Выполнив интегрирование, найдем ψ (t) =ω0t + (ωд /Ω)sin Ωt +θ0 . Таким образом:

a (t) = A0 cos ω 0 t + (ω д / Ω ) sin Ω t + θ 0 .

Фаза колебания a(t) наряду с линейно-возрастающим слагаемым ω (t ) содержит еще периодическое слагаемое (ωд / Ω )sin Ω t . Это позволяет

рассматривать a(t) как колебание, модулированное по фазе. Закон этой модуляции является интегральным по отношению к закону изменения частоты. Именно модуляция частоты по косинусноидальному закону приводит к модуляции фазы по закону синусоидальному. Амплитуду изменения фазы m = θ max = (ω д / Ω ) часто называют индексом угловой модуляции.

Заметим, что индекс модуляции совершенно не зависит от средней

(немодулированной) частоты ω0 , а определяется исключительно девиацией и модулирующей частотой.

При гармоническом модулирующем сигнале различие между ЧМ и ФМ можно выявить, только изменяя частоту модуляции. При ЧМ девиация ωд пропорциональна амплитуде модулирующего напряжения и не зависит от частоты модуляций. При ФМ величина θmax пропорциональна амплитуде

модулирующего напряжения и не зависит от частоты модуляции.

При ЧМ ωд, зависящая, как указывалось выше, только от амплитуды, будет, постоянной величиной, а индекс модуляции m=θmax =(ωд /Ω) с

увеличением частоты будет убывать. При ФМ m не зависит от Ω, а

ωд =θmaxΩ = mΩ изменяется пропорционально частоте модуляции.

Кроме структуры колебания (при модуляции сложным сигналом) частотная и фазовая модуляции различаются и способом осуществления. При ЧМ обычно применяется прямое воздействие на частоту колебаний генератора. При ФМ генератор дает стабильную частоту, а фаза колебания модулируется в одном из последующих элементов устройства.

Спектр колебания при угловой модуляции.

Пусть задано колебание

a(t) = A0 cos( ω0t +θ (t)) , о котором известно, что передаваемое сообщение s(t) заложено в функцию θ (t) . Если колебание a(t)

получено с помощью ФМ, то θ (t) и s(t) полностью совпадают по форме и отличаются лишь постоянным коэффициентом. При этом очевидно, с точностью до постоянного коэффициента совпадают и спектры функций

θ (t) и s(t)

При ЧМ функция θ (t) является интегралом от передаваемого сообщения s(t) . Так как интегрирование является линейным преобразованием, то при ЧМ спектр функции θ (t) состоит из тех же компонентов, что и спектр сообщения s(t) , но с измененными амплитудами и фазами.

Отвлекаясь от способа осуществления угловой модуляции — фазовой или частотной — и считая заданным спектр функции θ (t) , находим спектр модулированного колебания a(t). Для этого выражение

преобразуем к виду:

a(t) = A0 cos ω0t cos θ (t) − A0 sin ω0t sin θ (t) = ac (t) − as (t)

Отсюда следует, что модулированное по углу колебание можно рассматривать как сумму двух квадратурных колебаний: косинусного

ac(t) = A0 cosω0t cosθ (t)и синусного as(t) = A0 sin ω0tsinθ (t) каждое

из которых модулировано только по амплитуде; закон АМ для косинусного

колебания определяется медленной функцией функцией

Ранее было установлено, что для определения спектра амплитудномодулированного колебания достаточно сдвинуть на частоту ω0 спектр

огибающей амплитуд. Следовательно, для нахождения спектра колебания a(t), необходимо сначала найти спектры функций

спектры огибающих квадратурных колебаний. Перенос этих спектров на частоту ω0 можно затем осуществить таким же образом, как и при обычной

АМ.

Из приведенных рассуждений следует, что при одном и том же передаваемом сообщении спектр колебания, модулированного по углу, значительно сложнее, чем спектр модулированного по амплитуде. Действительно, так как cosθ (t) и sin θ (t) являются нелинейными функциями своего аргумента

θ (t), то спектры этих функций могут существенно отличаться от спектра функции θ (t); возможно возникновение кратных и комбинационных частот, как это имеет место при обычных нелинейных преобразованиях спектра.

Это обстоятельство, а также наличие двух квадратурных слагаемых показывают, что при угловой модуляции спектр модулированного колебания нельзя получить простым сдвигом спектра сообщения на величину несущей частоты ω0 , как это имеет место при АМ. При угловой модуляции связь

между спектрами сообщения и модулированного колебания оказывается более сложной.

При тональной модуляции

a(t) = A0 cos(ω0t +θ0msin Ωt +γ ) .

Это совпадает с ЧМ при ω(t) =ω0 +ωД cos(Ωt) Если θ0 = 0, , то получаем:

θ (t) = msin Ωt

a(t) = A0 cos(msin Ωt)cos(ω0t) − A0 sin(msin Ωt)sin(ω0t)

Разложим периодические функции (m sin Ωt) и (m cos Ωt) в ряд Фурье,

получим:

cos(msinΩt) = 2J1(m)sinΩt + 2J3 (m)sin3Ωt + 2J5 (m)sin5Ωt +..., sin(m sin Ωt) = J0 (m) + 2J2 (m) cos 2Ωt + 2J4 (m) cos 4Ωt + ...,

где Ji (m) - Бесселева функция первого рода, i-ого порядка от аргумента m. При подстановки в вышеприведенное выражение конкретной функции получим:

a(t) = A0(J0(m)cosω0t − 2J1(m)sinΩt sinω0t + 2J2(m)cos2Ωt cosω0t − 2J3(m)sin3Ωt sinω0t = A0 (J0(m)cosω0t + 2J1(m)(cos(ω0 + Ω)t − cos(ω0 − Ω)t)+ J2(m)(cos(ω0 + 2Ω)t − cos(ω0 − 2Ω + J3(m)(cos(ω0 + Ω)t − cos(ω0 − Ω)t)+...

То есть при ЧМ и ФМ спектр состоит из бесконечных чисел боковых частот попарно расположенных относительно ω0 и отличающихся на nΩ . Амплитуда n-ой боковой составляющей An = Jn (m)A0 , то есть вклад боковых частот в суммарную мощность модулированных колебаний определяется величиной m.

Если m<<1, то sin(msin Ωt) = msin(msin Ωt),cos(msin Ωt) = 1. Тогда:

a(t) = A0(cosω0t −msinΩtsinω0t) = A0(cosω0t + m/ 2cos(ω0 + Ω)t − m/ 2cos(ω0 − Ω)t)

.

Сравнивая с АМ колебанием:

A(t) = A0 (1+ M cos Ωt) и

a(t) = A0 (cosω0t − msin Ωt sinω0t) = A0 (cosω0t + m / 2cos(ω0 + Ω)t + m / 2cos(ω0 − Ω)t)

.

Боковая несущая частота (ω0 + Ω) противоположна по фазе другой боковой частоте при УМ.

При m =θmax <<1 ширина спектра равна 2Ω .

Если m=0.5-1, то в спектре возникает вторая пара боковых частот и

нуля.

В этом случае ширина спектра:

ШС = 2 nmax Ω = 2mΩ , где m = ωΩд , то есть ШС = 2ωд . Модуляция с m<<1 называется быстрой модуляцией

( ШС = 2Ω,ωд << Ω)

Модуляция с m>>1 называется медленной модуляцией ( ШС = 2ωд ,ωд >> Ω )

СПЕКТР КОЛЕБАНИЯ ПРИ АМПЛИТУДНО-ЧАСТОТНОЙ МОДУЛЯЦИИ

Пусть амплитуда задана функцией A(t):

a(t) = A(t)cos[ω0t +θ(t)]= A(t)cosθ(t)cosω0t − A(t)sinθ(t)sinω0t = ac (t) − as (t).

Определение спектра колебания сводится к нахождению спектров функций Ac (t) = A(t)cosθ(t) и As (t) = A(t)sinθ(t) , т. е. огибающих квадратурных колебаний, и к последующему сдвигу этих спектров на величину ω0.

Обозначим спектральные плотности функций Ac (t) и As (t) символами

SAc (ω) и SAs (ω) . Тогда:

∞

SAc (ω) = ∫A(t)cosθ(t)e− jωt dt,

−∞

∞

SAs (ω) = ∫A(t)sinθ(t)e− jωt dt,

−∞

Спектральная плотность косинусного квадратурного колебания ac (t) = Ac (t)cosω0t при θ = 0 будет

Sa(ω)=1/2[SAc (ω−ω0)+SAc (ω+ω0)].

При определении спектра синусного квадратурного колебания as (t) = As (t)cosω0t фазовый, угол θ = 900 . Следовательно,

Sa (ω) = − j/2[SAs (ω −ω0 )+ SAs (ω +ω0 )]..

В области положительных частот можно считать

SAc (ω+ω0) ≈ SAs (ω+ω0) ≈0.

Таким образом, окончательно спектральная плотность колебания

a(t) = ac (t)−as (t) определяется выражением

Sa(ω) = SAc (ω)−SAs (ω) =1/2[SAc (ω−ω0)+iSAs (ω−ω0)],ω >0.

Переходя к переменной Ω = ω − ω0 , получаем:

Sa (ω0 + Ω) =1/ 2[SAc (Ω) + SAc (Ω)].

Структура спектра колебания а(t) при амплитудно-частотной модуляции зависит от соотношения и вида функций A(t) и θ(t).

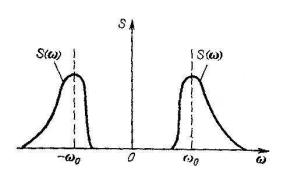
При АМ спектр колебания а(t) характеризуется полной симметрией амплитуд и фаз колебаний боковых частот относительно несущего колебания; при угловой модуляции фазы колебаний нижних боковых частот при нечетных п сдвинуты на 180°. Одновременная модуляция по амплитуде и углу может при некоторых соотношениях между A(t) и θ(t) приводить к асимметрии спектра

S0(ω0 +Ω) относительно ω0 не только по фазам, но и по амплитудам. В

частности, если θ(t) является нечетной функцией t, то при любой функции A(t) спектр колебания а (t) несимметричен.

Пример подобного спектра представлен на рисунке. (По отношению к точке ω = 0 модуль спектральной плотности симметричен при любых условиях.)

Для симметрии спектра S0 (ω)

требуется четность функции θ(t) при одновременном условии, чтобы функция A(t) была либо четной, либо

нечетной функцией t. Если функция A(t) может быть представлена в виде суммы четной и нечетной составляющих, то спектр S0 (ω) несимметричен даже при четной функции θ(t).

Наглядное представление о деформации спектра колебания при смешанной модуляции — амплитудной и угловой — можно получить, рассмотрев случай, когда обе модуляции осуществляются гармонической функцией с одной и той же частотой •. Для упрощения анализа зададим эту функцию в виде гармонического колебания cosbt для угловой модуляции и в виде cosbt или sinbt для амплитудной.

Рисунок

иллюстрирует

спектр колебания при одновременной модуляции амплитуды и частоты гармонической функцией

1. Обе функции, как А(t), так и b(t), четные относительно t:

a(t) = A0 (1+ M cos Ωt)cos[ω0t + mcos Ωt].

Приводим это выражение к виду:

Суммируя квадратурные составляющие cosω0t и (mM/2)sinω0t, получаем для амплитуды результирующего колебания на частоте ω0 следующее

ω0±2•. Спектр колебания для рассматриваемого случая, представленный на рис.а, симметричен.

2. Функция •(t) — четная, а A(t) содержит четную и нечетную составляющие:

A(t) = A0 (1+ M sin Ωt),θ (t) = mcosΩt,M ≤ 1,m ≤ 1.

Выкладки, аналогичные предыдущим, приводят к следующим результатам: амплитуда равна 1 на частоте ω0; 1/2(М—т) на частоте ω0—•; 1/2(М +m) на частоте ω0—•; тМ/4 на частотах ω0±2•. Спектр колебания для рассматриваемого случая представлен на рис.б. Симметрия спектра нарушается в данном примере из-за неодинаковых амплитуд колебаний верхней и нижней боковых частот.

Асимметрия спектра при амплитудно-угловой модуляции может рассматриваться как показатель неправильной работы устройства, осуществляющего АМ; перекос спектра указывает на то, что полезная АМ сопровождается паразитной угловой модуляцией.

ЛЧМ – сигнал и его спектр.

При модуляции частоты колебания по закону, отличающемуся от гармонического, нахождение спектра колебания усложняется. Выбор наиболее удобного метода анализа зависит от характера модулирующей функции. Поясним один из возможных методов на примере широко распространенного сигнала — импульса с линейной частотной модуляцией (ЛЧМ импульса). Подобный сигнал изображен на рисунке сверху, а закон изменения частоты

заполнения импульса — на рисунке снизу.

Мгновенную частоту заполнения ω(t) = 2πf (t)

можно определить выражением

ω(t) =ϖ0 + βt,|t |≤Te /2,