Радиотехнические цепи и сигналы

•

можно сохранить прежним, а изменить только аргумент, так что K(ω)

• •

перейдет в K(p) . Функция же E(ω) переходит в L[E( p)]. Преобразование

Лапласа от функции времени е (t) в дальнейшем обозначается символом

•

E( p). При этом получаем:

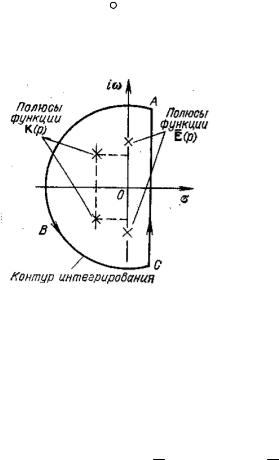
При t > 0 замкнутый контур интегрирования, образованный добавлением дуги бесконечно большого радиуса в левой полуплоскости, охватывает все

полюсы подынтегральных функций как E( p), так и K(p) , благодаря чему имеет место соотношение:

•

соответствует ЭДС вида e(t) = EΩ cosω0t, существующей при t ≥0.

Итак, вычисление интеграла сводится к определению вычетов в полюсах подынтегральной функции. Представим подынтегральную функцию

• •

выражения в виде: E(p)K(p)ept =U(p)ept =C(p)/D(p).

В данном случае знаменатель D(p) образуется произведением множите-

•

лей вида ( p — pi ), где pi — полюсы не только функции K(p) , но и функ-

ции E(p).

Тогда вычет функции С(p)/D(p), имеющей в точке рi простой полюс (первой кратности), определится формулой

Если функция C(p)/D(p) имеет в точке рi полюс кратности k (k — целое положительное число), то

Методика применения контурных интегралов для определения некоторых функций, играющих большую роль в теории переходных процессов, будет в дальнейшем пояснена на примерах.

Метод интеграла наложения.

Вместо разложения сложного сигнала на гармонические составляющие (спектральный метод) можно воспользоваться разбиением сигнала на достаточно короткие импульсы (рис. а).

Если в основе спектрального метода лежит передаточная функция цепи

•

K(ω), то метод интеграла наложения базируется на импульсной характеристике цепи g(t) .

Пусть требуется найти сигнал sвых (t) на выходе цепи, если задан сигнал s(t) на входе цепи и известна ее импульсная характеристика g(t) . Для уяснения сути метода интеграла наложения поступим следующим образом.

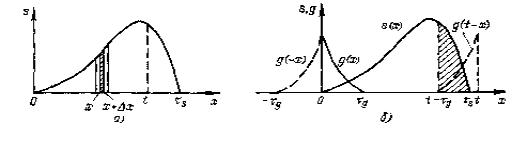
Разобьем произвольный сигнал на элементарные импульсы, как это по-

казано на рис. а, и найдем отклик цепи в момент t на элементарный импульс (на рис. а заштрихован), действующий на входе в момент x. Если бы площадь этого импульса равнялась единице, то импульс можно было бы рассматривать как дельта-функцию, возникшую в момент x. При импульсной характеристике цепи g (t) отклик в момент t был бы, очевидно, равен

g (t − x) . Поскольку, однако, заштрихованная на рис. 6.2, а площадь импульса равна s(x) x (а не единице), отклик в момент t будет

s(x) xg (t − x) .

Для определения полного значения выходного сигнала в момент t нужно просуммировать действие всех импульсов в промежутке от x = 0 до x = t. При

x → 0 суммирование сводится к интегрированию. Следовательно,

В общем случае, если начало сигнала s(x) не совпадет с началом отсчета времени x, последнее выражение можно записать в форме

Рис. Разбиение сигнала на короткие импульсы (а) и свертка сигнала с импульсной характеристикой (б).

Для реальных цепей всегда выполняется условие g (t − x) = 0 при t < x,

т. е. при отрицательном аргументе функция g (t − x) должна обращаться в нуль, так как отклик не может опережать воздействие. Поэтому выражение

sвых (t) = t∫ s(x)g(t− x)dx можно заменить выражением:

0

(при этом имеется в виду, что для x > t подынтегральное выражение обращается в нуль).

Приведем, наконец, еще одну форму записи, которая получается из выра-

Интеграл, стоящий в правой части этого выражения, в математике называется сверткой функций s(t) и g(t) . Таким образом, приходим к следующему важному положению: сигнал sвых (t) на выходе линейной цепи является

сверткой входного сигнала s(t) с импульсной характеристикой цепи g(t) . Также из этого выражения видно, что сигнал на выходе цепи sвых (t) в

момент t получается суммированием мгновенных значений входного сигнала s(t) , взятых с весом g (t − x) за все предыдущее время.

При суммировании спектра входного сигнала весовой функцией являлась

•

передаточная функция цепи K(ω). В данном случае при суммировании мгновенных значений входного сигнала s(t) весовой функцией является импульсная характеристика цепи, взятая с аргументом (t − x) , т. е. функция g (t − x) .

Из рис. б, построенного для момента времени t >τ s , видно, что отклик цепи на воздействие s(x) не может закончиться раньше, чем функция g (t − x)

сместится вправо от s(x) на время, равное длительности импульсной характеристики τ g . Иными словами, сигнал на выходе цепи не может быть

короче τs +τs .

Для того чтобы при прохождении через цепь сигнал не удлинялся, требуется выполнение условия τ g → 0 , т. е. импульсная характеристика цепи должна

приближаться к дельта-функции, а это равносильно требованию рав-

•

номерности передаточной функции K(ω), при 0 < ω < ∞ .

Метод огибающей.

В рассмотренных в предыдущей главе задачах мы имели дело с сигналами, которые по своей форме совпадали с формой передаваемого сообщения. При передаче подобных сообщений задача сохранения информации тесно связана с задачей сохранения формы сигналов. Иначе обстоит дело с радиосигналом, в котором информация заключена

водном из нескольких параметров высокочастотного колебания. Не обязательно сохранять полностью структуру этого колебания; достаточно лишь сохранить закон изменения того параметра, в котором заключена информация. Так, в случае амплитудно-модулированного колебания важно точно передать огибающую амплитуд, между тем как некоторое изменение частоты или фазы заполнения, не имеющее существенного значения, при анализе можно не учитывать. При передаче радиосигналов с угловой модуляцией, наоборот, основное внимание следует уделить точному воспроизведению закона изменения частоты и фазы.

Эти особенности радиосигналов открывают путь к упрощению методов анализа передачи их через линейные цепи. Возможность упрощения особен-

но существенна, когда радиосигнал представляет собой узкополосный процесс, а цепь — узкополосную систему. Это как раз и характерно для реальных радиосигналов и реальных избирательных цепей. Ранее отмечалось, что даже для «широкополосных» сигналов ширина спектра радиосигнала мала по сравнению с несущей частотой сигнала. Соответственно и полоса прозрачности цепи обычно мала по сравнению с ее резонансной частотой. Анализ передачи сигнала в подобной ситуации существенно упрощается при использовании понятия аналитического сигнала:

z(t) = a(t) + ja1(t) = A(t)eiω 0t ,

где комплексная огибающая A(t) содержит всю информацию, заложенную в сигнал в результате модуляции, как амплитудной, так и угловой.

После прохождения через заданную цепь получается новый аналитический сигнал:

z (t) = a (t ) + ja 1 (t) = A(t)eвыхjθ e jω 0 t , действительная часть которого: aвых (t) = Re zвых (t) = Aвых (t)cos( ω 0t + θ вых (t)) и есть выходной сигнал. Таким образом, задача сводится к определению влияния цепи на комплексную огибающую входного сигнала.

Эта задача может быть решена двумя способами: спектральным и временным.

1) Спектральный метод.

Спектральная плотность высокочастотного модулированного колебания образует два всплеска вблизи частот ω0 и −ω0 , а передаточная функция

•

K(ω) — вблизи частот ω0 и −ω0 . Для общности здесь принято, что резонансная частота может не совпадать с центральной частотой сигнала ω0 ,

т. е. может иметь место расстройка. При этом предполагается, что расстройка является величиной того же порядка, что и полоса прозрачности цепи.

Спектральная плотность сигнала Z(ω) = 2Sa(ω) отлична от нуля только в области положительных частот. Очевидно, что:

Sa (ω ) ≈ 12 S A (ω − ω0 ), S A - спектральная плотность огибающей.

Подставив это выражение в предыдущее, получим:

zвых(t)= 1 ∞∫ SA(ω−ω0 ) K• (ω)e jωt dω . 2π 0

Перейдем к новой переменной Ω =ω −ω0. Тогда:

Выражение, стоящее в фигурных скобках, соответствует комплексной огибающей выходного колебания

Дальнейшее упрощение анализа вытекает из свойств передаточной функции резонансных цепей, обладающих сильно выраженной частотной изби-

•

рательностью. Модуль передаточной функции K(ω) быстро убывает при удалении ω от резонансной частоты ωр . Поэтому передаточную функцию

целесообразно выражать в виде функции разности ω0 −ωр .

Введем новое обозначение передаточной функции:

aвых(t)= ∞∫ a(x)g(t−x)dx

−∞

•

где a(t) = A(t)cos(ω0t +θ(t)) = Re(A(t)e jω0t ), а

Вторым интегралом можно пренебречь по сравнению с первым из-за наличия

быстропеременного множителя с частотой ω0 + ω р . Переходя к комплексной форме, получаем:

соответственно входного сигнала и импульсной характеристики фильтра, приходим к следующему выражению: