
Радиотехнические цепи и сигналы
.pdf
Спектр последовательности треугольных импульсов
∞
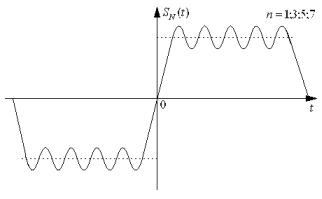
При N → ∞ сумма ряда ∑ An cos(nΩ1t − Ψn ) приближается к s(t) всюду,
n−1
кроме точек разрыва функции, где образуются выбросы.
При n→∞ величина этого выброса равна 1,18E. Этот дефект сходимости (18%) носит название явления Гиббса. Но ряд сходится в среднем, то есть выбросы бесконечно узкие и не вносят ощутимого вклада в усреднение.
 .
.
Распределение мощности в спектре периодического сигнала.
|
|
|
|
|
|
|
a |
0 |
|
2 |
|
|
1 |
∞ |
|
|
|
|
|
|
|
|
|||||
|
|
|
S (t) = |
|
|
|
|
|
+ |
|
|
∑ an cos( nΩ 1t) + bn |
cos( nΩ 1t) |
||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
||||||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
n =1 |
|
|
|
|
|
. |
|||||||
|
|
|
|
|
a |
0 |
|
|
2 |
|
|
1 |
|
∞ |
|
|
|
|
|
1 |
∞ |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
S 2 (t) = |
|
|
|
|
|
|
+ |
|
|
∑ |
(an2 + bn2 ) = A02 + |
|
∑ An2 |
|
|||||||||||||
|
2 |
|
|
2 |
2 |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
n=1 |
|
|
|
|
|
n=1 |
. |
|||||||||
|
|
|
Если S(t) = i(t) |
– ток, то мощность, выделяемая на сопротивлении R. |
|||||||||||||||||||||||
|
P = Ri |
|
2 (t) = 2(I0 + |
|
I12 |
+ |
I22 |
+ |
I32 |
+ ...) . |
|
|
|
||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
2 |
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
2 |
|
|
|
|
|||
|
|
|
|
|
|
|
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
2 (t) = 1 ∑ An2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
S |
. Средняя мощность не зависит от фаз отдельных |
||||||||||||||||||||||||||
|
|
|
|
|
4 n=−∞ |
|
|
||||||||||||||||||||
гармоник.
Гармонический анализ непериодических сигналов
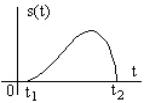
Пусть сигнал s(t) задан в виде некоторой функции, отличной от нуля в промежутке (t1, t2). Этот сигнал должен быть интегрируем на интервале (t1, t2).
Возьмем бесконечный отрезок времени Т, включающий в себя промежуток (t1, t2). Тогда сигнал S(t) является, как бы периодическим с
периодом T→ ∞, а Ω1 = 2π → 0 .
T
Заданный сигнал можно представить в виде ряда Фурье, где
|
|
|
|
|
T |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 t2 |
|
|
||
& |
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
||||
An = an − |
jbn = |
|
|
∫ |
s(t)[cos nΩ1t − j sin nΩ1t |
]dt |
= |
|
|
∫ |
s(t) exp( − jnΩ1t)dt |
|||||||
T |
|
T |
||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
− |
T |
|
|
|
|
|
|
|
|
t1 |
|
|
||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|||
На основании этого получим: |
|
|
|
|
|
|
|
|
|
|
||||||||
∞ |
1 |
t2 |
|
|
|
|
|
|
|
1 |
|
∞ |
t2 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
s(t) = ∑ |
|
∫s(t)exp(− jnΩ1t)dt |
exp( jnΩ1t) = |
|
|
∑ |
∫s(t)exp(− jnΩ1t)dt |
exp( jn |
||||||||||
T |
2π |
|
||||||||||||||||
n=−∞ |
|
t1 |
|
|
|
|
|
|
|
|
|
n=−∞ t1 |
|
|
|
|||
Поскольку Т→, то сумму можно заменить интегралом, а Ω1 на dΩ и nΩ1 на Ω. Таким образом, мы прейдем к двойному интегралу Фурье:
|
1 |
∞ t2 |
− jΩt |
|
|
|
||
|
|
|
|
|
|
|
||
s(t) = |
2π |
∫ |
∫ s(t)e |
|
|
dt |
exp( |
jΩt)dΩ , |
|
− ∞ t1 |
|
|
|
|
|
||
t2 |
|
|
|
|
|
|
|
|
Где S&(Ω)∫s(t)e− jΩt dt — спектральная |
плотность |
сигнала. Когда интервал |
||||||
t1 |
|
|
|
|
|
|
|
|
(t1,t2) не уточнен, интеграл имеет бесконечные пределы.
Это есть обратное и прямое преобразование Фурье, соответственно. Спектр непериодического сигнала является сплошным
• |
|
|
S (Ω) = ∫ s(t)e− jΩt dt |
||
|
|
|
|
1 ∫ S (Ω)e− jΩt dΩ |
|
s(t) = |
||
|
|
• |
|
|
|
2π |
||
|
|
|

Если сравнить выражения для огибающей сплошного спектра (модуль спектральной плотности) непериодического сигнала и огибающей линейчатого спектра периодического сигнала, совпадающего на интервале (t1,t2) с непериодическим сигналом, то будет видно, что они совпадают по форме.
Учитывая, что Ω = nΩ1 , получим:
t2 |
|
& |
2 |
|
t2 |
|||
S& (Ω ) = ∫ s (t ) exp( − jn Ω 1t )dt |
, An |
= |
|
|
|
∫ s(t ) exp( − jn Ω 1t )dt |
||
T |
|
|||||||
t1 |
|
|
|
|
|
|
|
t1 |
& |
= |
|
2 S& (Ω ) |
|
|
|
||
но отличаются масштабами An |
|
|
T |
. |
||||
|
|
|
|
|
|
|||
Следовательно, спектральная плотность S&(Ω) обладает всеми основными свойствами комплексного ряда Фурье. Т. е. можно записать
S&(Ω) = A(Ω) − jB(Ω) = S(Ω) exp( − jϕ (Ω)) ,
∞ |
∞ |
где A(Ω ) = ∫ s(t) cos Ω tdt , |
B(Ω) = ∫s(t)sinΩtdt , |
− ∞ |
−∞ |
∞ |
∞ |
спектральная плотность: S(Ω) = ∫s(t)cos(Ωt)dt − j ∫s(t)sin(Ωt)dt
−∞ −∞
Модуль спектральной плотности S(Ω) = |
A2 (Ω) + B2 (Ω) является |
четной функцией и его можно рассматривать |
как амплитудно-частотную |
характеристику сигнала. Аргументϕ(Ω) = −arctg B(Ω) A(Ω) — нечетная функция, рассматриваемая как фазо-частотная характеристика сигнала.
На основании этого сигнал можно выразить следующим образом
|
1 |
∞ |
• |
1 |
∞ |
• |
j |
∞ |
|
s(t) = |
∫S(Ω)ejΩt dΩ = |
∫S(Ω)cos(Ωt −ϕ)dΩ + |
∫S(Ω)sin(Ωt −ϕ)dΩ |
||||||
2π |
2π |
2π |
|||||||
|
−∞ |
|
−∞ |
|
−∞ |
||||
|
|
|
|
|
|
||||
Из четности модуля и нечетности фазы следует, что подынтегральная функция в первом случая является четной, а во втором — нечетной относительно Ω. Следовательно, второй интеграл равен нулю (нечетная функция в симметричных пределах) и окончательно
|
1 |
∞ |
• |
1 |
∞ |
• |
1 |
∞ |
|
s(t) = |
|
S(Ω)e jΩt dΩ = |
|
S(Ω)cos(Ωt −ϕ)dΩ = |
|
S(Ω) cos(Ωt −ϕ)dΩ . |
|||
2π ∫ |
2π ∫ |
π |
∫ |
||||||
|
|
−∞ |
|
|
−∞ |
|
|
0 |
|
Отметим, что при Ω=0 выражение для спектральной плотности равно площади под кривой s(t)
• |
t2 |
S (0) = |
∫ s(t )dt , |
|
t1 |
то есть S&(0) имеет значение, равное площади сигнала.
Свойства преобразования Фурье
Сдвиг сигнала во времени
Пусть сигнал s1(t) произвольной формы обладает спектральной плотностью S1(Ω). При задержке этого сигнала на время t0 получим новую функцию времени s2(t)=s1(t-t0). Спектральная плотность сигнала s2(t)
• |
t2 +t0 |
t2 +t0 |
|
S 2 (Ω) = |
∫s2 (t)e− jΩt dt = ∫s1(t − t0 )e− jΩt dt . |
||
|
t1 +t0 |
t1 +t0 |
|
Введем новую переменную τ=t−t0. Отсюда |
|||
|
• |
t2+t0 |
• |
|
S2 (Ω) = |
∫ |
s1(τ)e− jΩte− jΩt0 dt = e− jΩt0 S1(Ω). |
|
|
t1+t0 |
|
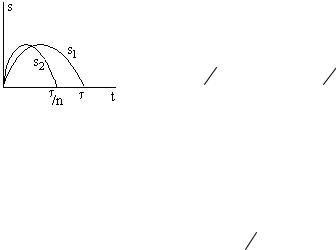
Сдвиг сигнала по оси времени приводит к изменению фазы спектральная плотность, а модуль не зависит от положения сигнала на оси времени.
Изменение масштаба времени
Пусть сигнал s1(t) подвергается сжатию во времени. Новый сигнал s2(t) связан с исходным соотношением s2(t) =s1(nt),где nf1.
Длительность импульса s2(t) в n раз меньше, чем исходного. Спектральная плотность сжатого импульса
|
|
τ |
τ |
• |
|
n |
n |
S 2 |
(Ω) = |
∫s2 (t)e− jΩt dt = ∫s1(nt)e− jΩt dt . |
|
|
|
0 |
0 |
Введем новую переменную τ =nt. Получим
|
τ |
Ω |
|
1 |
τ |
Ω |
1 • |
|
• |
n |
|
||||||
|
− j nt 1 |
|
− j |
τ |
||||
S(Ω) = ∫s1(nt)e |
n |
ndnt= n |
∫s1(τ)e |
n |
|
dτ = nS1(Ω/n). |
||
|
0 |
|
|
|
0 |
|
|
|
При сжатии сигнала в n раз во столько же раз расширяется его спектр. Модуль спектральной плотности при этом уменьшается в n раз. При растяжении сигнала во времени имеют место сужение спектра и увеличение модуля спектральной плотности.
Смещение спектра колебаний
Домножим сигнал s(t) на гармонический сигнал cos(ω0t+θ0). Спектр такого сигнала
∞ |
|
∞ |
|
1 |
|
j(ω0t+θ0 ) |
|
1 |
|
j(ω0t+θ0 ) |
|
|
S2 (Ω) = ∫s(t)cos(ω0t + θ0 )e |
− jΩt |
|
e |
+ |
e |
jΩt |
dt |
|||||
|
dt = ∫s(t) |
2 |
|
2 |
e |
|
||||||
−∞ |
|
−∞ |
|
|
|
|
|
|
|
|
||
Разобьем его на 2 интеграла

S2 |
(Ω) = |
e jθ0 |
∞ s(t)e |
− j(Ω−ω0 )t dt + |
e− jθ0 |
∞ s(t)e− j(Ω−ω0 )t dt . |
|
|
|||||
|
2 |
∫ |
2 |
∫ |
||
|
|
|
−∞ |
|
|
−∞ |
Полученное соотношение можно записать в следующей форме
S• 2 (Ω) = 12 e jθ0 S• (Ω −ω0 ) + 12 e− jθ0 S• (Ω + ω0 )
Таким образом, умножение функции s(t) на гармоническое колебание приводит к расщеплению спектра на 2 части, смещенные на ±ω0.
Дифференцирование и интегрирование сигнала
|
|
Пусть |
дан сигнал s1(t) со спектральной |
плотностью S1(Ω). |
||||
Дифференцирование этого сигнала s2 (t) = ds1 (t) |
dt |
дает соотношение |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
• |
|
|
• |
|
|
|
|
|
S2 (Ω) |
= jΩ S1 (Ω) . |
|
||
Интегрирование |
сигнала s2 (t) = ∫s1 (t)dt |
|
приводит |
к выражению |
||||
• |
|
1 |
• |
|
|
|
|
|
S |
2 |
(Ω) = |
|
S1 (Ω) |
|
|
|
|
jΩ |
|
|
|
|
||||
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
.
Сложение сигналов
При сложении сигналов s1(t) и s2(t) обладающих спектрами S1(Ω) и S2(Ω) суммарному сигналу s1(t)+s2(t) соответствует спектр S1(Ω)+S2(Ω) (т. к. преобразование Фурье является линейной операцией).
Произведение двух сигналов
Пусть S(t) представлен произведением двух сигналов: s(t) = f (t)g(t). Такому сигналу соответствует спектр
∞ |
∞ |
S (Ω ) = ∫ s(t)e − jΩ t dt = ∫ f (t) g (t)e − jΩt dt |
|
− ∞ |
− ∞ |
Представим функции в виде интегралов Фурье
|
|
|
|
1 |
∞ • |
|
|
|
|
|
|
|
1 |
|
∞ • |
|
|||
|
|
f (t) = |
∫ |
F(Ω)e jΩt dΩ , g(t) = |
|
|
∫ |
G(Ω)ejΩtdΩ. |
|||||||||||
|
|
2π |
|
2π |
|||||||||||||||
|
|
|
|
|
−∞ |
|
|
|
|
|
|
|
|
|
|
|
−∞ |
|
|
|
• |
|
• |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Где F(Ω)иG(Ω)−спектральная плотность сигналов f(t) b g(t) |
|||||||||||||||||||
соответственно. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Подставляя второй интеграл в выражение для S(Ω) получим |
|||||||||||||||||||
|
1 |
∞ |
∞ |
|
|
|
|
|
1 |
|
|
∞ |
|
∞ |
|
||||
S(Ω) = |
∫ |
f (t) ∫G(x)e− jxt dx e− jΩt dt = |
|
|
∫G(x) ∫ |
f (t)e− j(Ω− x)t dt dx |
|||||||||||||
2π |
|
2π |
|
||||||||||||||||
|
−∞ |
−∞ |
|
|
|
|
|
|
|
−∞ |
|
−∞ |
|
||||||
Следовательно |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
1 |
|
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S (Ω ) = |
2π |
∫ |
G ( x)F |
(Ω − x)dx . |
|
||||||||||
|
|
|
|
|
|
|
|
||||||||||||
−∞
Т. е. спектр произведения двух функций времени равен свертке их спектров (с коэффициентом 1/2π).
|
∞ |
|
|
|
|
Если |
s(t) = ∫ f (τ )g(t −τ )dτ , |
то |
спектр |
сигнала |
будет |
|
−∞ |
|
|
|
|
S(Ω) = F(Ω)G(Ω) .
Взаимная обратимость частоты и времени в преобразовании Фурье
1. Пусть s(t) — четная функция относительно времени.

∞
Тогда S&(Ω) = 2∫s(t)cos(Ωt)dt . То есть функция S&(Ω) = S(Ω) является
0
вещественной и четной относительно Ω.
2. Пусть s(t) — нечетная функция относительно времени. При этом:
• |
∞ |
|
|
S(Ω) = − j ∫s(t)sinΩtdt . |
|
|
−∞ |
Вэтом случае S(Ω) является нечетной и чисто линейной.
3.Пусть s(t)=s1(t)+s2(t), где s1(t) и s2(t) – четная и нечетная функции соответственно. При этом
S(Ω) = S1(Ω)− jS2(Ω),
4. Предположим, что s(t) — четная функция. Запишем s(t) в виде
|
2π |
∞ |
• |
|
∫ |
|
|
s(t) = |
1 |
|
S (Ω )e jΩt dΩ . Произведем замену Ω на t и t на Ω, учтем, что |
|
−∞ |
||
|
|
|
S(t) – в данном случае вещественная функция, получим:
s(Ω) = 1 ∞∫S• (t)e− jΩt dt .
2π −∞
Таким образом, если сигнал, совпадает по форме с нашим исходным, то его спектр повторяет форму исходного сигнала.
Предыдущий раздел |
Раздел верхнего уровня |
Примеры спектров непериодических сигналов
Прямоугольный импульс
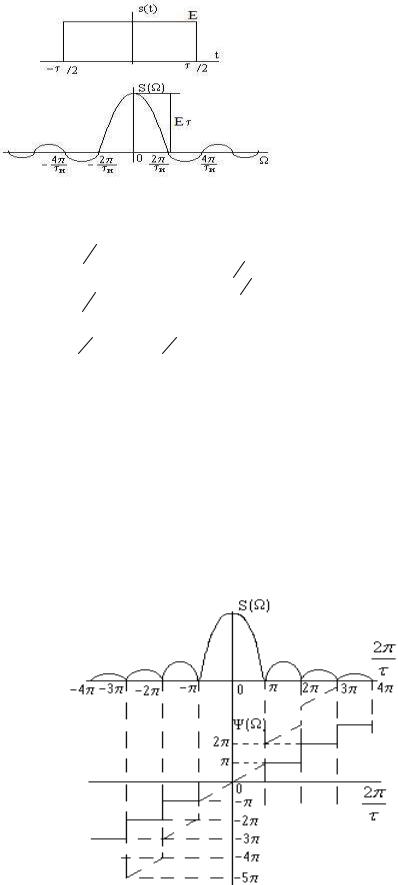
Определяется выражением
|
E при |
− |
τ |
≤ t ≤ |
τ |
||
|
2 |
2 |
|||||
s(t)= |
|
p |
|
|
τ |
|
f τ |
|
|
− |
и t |
||||
0 при t |
|
2 |
2 |
||||
|
|
|
|
|
|
||
|
|
|
−τ 2 |
2 |
E |
|
τ |
|
|||
S&(Ω) = E ∫e jΩtdt = |
|
|
|||||||||
|
|
||||||||||
|
e− jΩt |
|
−τ22 |
= |
|||||||
− jΩ |
|||||||||||
|
|
|
|
||||||||
|
|
|
−τ1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
2 E e j (τ 2 )Ω − e− j (τ 2 )Ω |
|
|
|
|||||||
= |
|
|
|
|
|
= |
|
|
|
||
Ω |
|
|
2 |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|||
Найдем спектральную плотность
|
sin |
Ωτ |
|
Ωτ |
|
|
Ωτ |
|
2 |
τ = Eτ sin c |
& |
|
|||
= E |
|
|
= S |
(0)sin c |
|
||
Ωτ |
2 |
2 |
|||||
|
|
2 |
|
|
|
|
|
