
Радиотехнические цепи и сигналы
.pdf
Энергетический расчет полосы пропускания – выбираем Ω ïð , исходя
из K эдоп |
= |
|
Эпр |
|
, |
|
|
|
|
|
Эmax |
|
|
|
|||||
|
|
|
|
|
|
|
|||
|
|
1 |
Ωпр |
1 |
∞ |
[S(Ω)]2 dΩ . |
|||
где Эпр |
= |
|
∫ |
[S(Ω)]2 dΩ , а Эmax = |
∫ |
||||
2π |
|
2π |
|||||||
|
|
|
|
−Ωпр |
|
−∞ |
|||
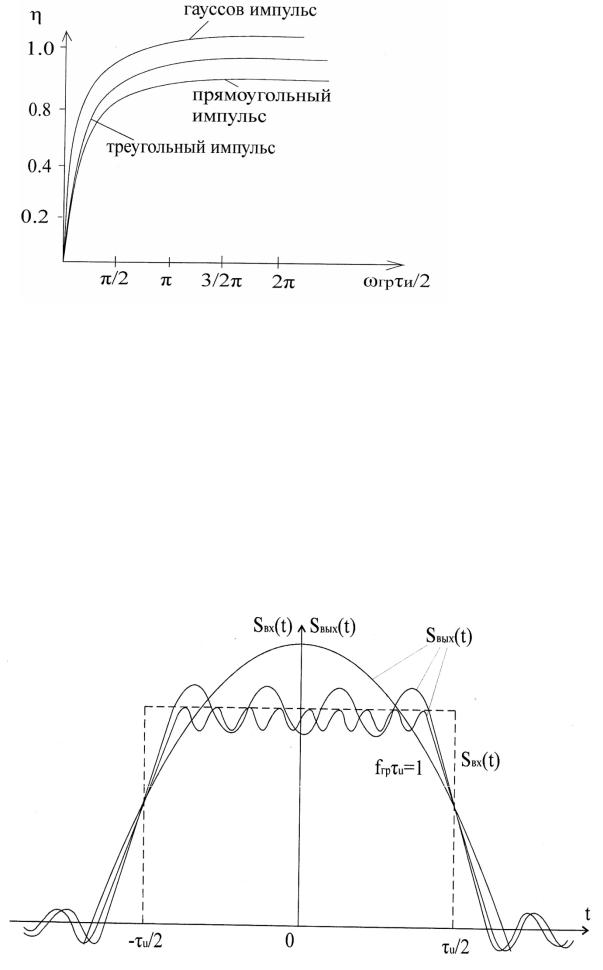
Соотношение между длительностью сигнала и широтой его спектра
Чем меньшеτ u , тем шире спектр |
f . |
||||||||||||
Для прямоугольного импульса |
f = |
|
1 |
|
содержит 90% энергии. |
||||||||
τ |
u |
||||||||||||
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
∞ |
|
|
|
|
1 2 |
||||
|
τ |
|
|
∫ t 2 S 2 ( t ) dt |
|
|
|
|
|
||||
Принято |
|
= |
− ∞ |
|
|
|
|
|
|
|
|
||
|
u |
|
∞ |
|
|
|
|
|
|
|
|
||
|
|
|
|
∫ |
|
2 ( t |
) dt |
|
|
|
|
|
|
|
|
|
|
|
S |
|
|
|
|
|
|||
|
|
|
|
− ∞ |
|
|
|
|
|
|
|
|
|
Примем начало отсчета, совмещенным с серединой импульса:
∞
∫tS 2 (t)dt = 0
−∞
ΔΩ = 2π f

|
|
|
1 |
∞ |
|
|
|
|||
|
|
|
|
|
∫ Ω 2 |
S 2 |
(Ω )dΩ |
|||
(ΔΩ ) |
|
2π |
||||||||
2 |
= |
|
|
− ∞ |
|
|
|
|||
|
|
|
|
|
1 |
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
∫ S |
2 (Ω )dΩ |
|||||
|
|
|
2π |
|||||||
|
|
|
|
|
|
− ∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
∞
При ∫ ΩS 2 (Ω )dΩ = 0
∞
Если S(t)нормировано так, что Э=1, то
∞
τ u2 = ∫ t 2 S (Ω )dt
− ∞ |
|
|
|
|
1 |
∞ |
|
(ΔΩ ) 2 = |
∫ Ω 2 S 2 (Ω )dΩ |
||
2π |
|||
|
− ∞ |
||
|
|
1
При этом τu ΔΩ ≥ 2 ,
1 т.е. τu f ≥ 4π
Для гауссовского импульса
τ u2 |
= |
|
π |
|
|
a 2 E 2 , |
|
|
|
|
|
|
|
|
|
||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
E 2 |
|
|
|
|
|
|
|
|
|
|
||||
(ΔΩ)2 = |
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
τ |
|
ΔΩ = |
|
|
|
π |
aE2 |
|
|
|
|
|
|
|
|
|
|||||||
u |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∞ |
∞ |
−t2 |
|
|
Используя условие нормировки Э = ∫S2 (t)dt = E2 ∫e |
a2 dt = πaA2 =1, |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−∞ |
−∞ |
|
|
|
Получим |
τ u |
ΔΩ = |
1 |
,τ u |
f = |
1 |
. |
|
|
|
|
||||||||||||
2 |
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4π |
|
|
|
|
||
Т.е. Гауссов импульс обладает наименьшей величиной произведений
τu f

Сжатие импульса во времени для повышения точности измерений момента его сопровождается расширением спектра импульса, что требует расширения полосы пропускания измерительного устройства.
Сжатие спектра импульса для повышения точности измерений частоты ведет к расширению сигнала во времени, что требует увеличения времени наблюдений. Невозможность концентрации сигнала в узкой полосе частот и коротким интервалом времени - проявление принципа неограниченности.
Эгр |
|
Ω грτ u |
|
2 Ω1τ u 2 |
sin 2 |
x |
|
|
|||
|
= η |
|
|
= |
|
∫ |
|
2 |
|
dx |
- определяет относительную |
|
|
|
|
|
|||||||
Эmax |
|
2 |
|
|
π |
x |
|
|
|||
|
|
|
0 |
|
|
|
|
||||
долю энергии сигнала в полосе частот 0 Ωгр
|
|
|
|
|
|
|
|
|
|
|
|
Ω τ |
u |
|
2 |
|
|
|
|
|
|
1 |
= |
|
sin |
|
|
и − |
||||
η |
|
|
|
|
ω |
грτ |
||||
2 |
|
π |
||||||||
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin |
2 |
|
ω |
|
τ и |
|
|
|
||
|
|
гр |
|
2 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
τ и |
|
|
|
|||
|
ωгр |
2 |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Для треугольного импульса
η (ω гр |
τ 4 )= |
|
|
ω грτ и |
|
|
|
3 |
4 |
4 |
|
||||
|
∫ |
sinx 4 |
x dx |
||||
π |
|||||||
|
|
|
0 |
|
|
||
Для Гауссовского имульса
|
|
|
|
aωгр |
|
|
|
|
|
|
ωгрτu |
|
|
|
|
|
|
|
|
2 |
|
−x |
2 |
2 |
2 |
|
−x |
2 |
|
ω τ |
|
|
|||||
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
гр |
u |
|||||||
η(aωгр )= |
|
|
|
∫e |
|
dx = |
|
|
|
|
∫e |
|
|
dx =Ф(aωгр )=Ф |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
||||||||
|
π |
|
π |
|
|
|||||||||||||
|
|
0 |
|
|
0 |
|
|
|
|
|
|
|||||||
Где Ф(x) - интервал вероятности
Произведение |
fгрτи при заданной η максимально для прямоугольного |
|||
импульса и минимально для гауссово импульса. |
|
|||
При η =0,95 |
|
|
|
|
|
|
|
|
|
Вид импульса |
|
прямоугольный |
треугольный |
Гауссов |
|
|
|
|
|
fгр τu |
|
1,8 |
0,94 |
0.48 |
Для сокращения прямоугольной формы входного импульса необходимо fгр τu ff1

Скорость убывания спектра вне основной полосы
δ (t)-единичная функция, имеющая неубывающую спектральную
плотность на всей оси частот • (ω ) = 1
S δ
Сигнал, спектр которого вне основной полосы не убывает с ростом и содержит в своем составе дельта-функцию (или мощный короткий импульс).
1(t)-единичная функция, имеющая S(ω)= ω1 , т.е. убывание хвоста спектра сигнала S(t) по закону ω1 говорит о наличие в S(t) скачков, т.е. разрывов непрерывности. В точках разрыва S′(t)=δ(f ), поэтому убывание спектра по закону ω1 указывает на наличие дельта функции в составе S′(t).
То же следует для производных высших порядков. Примеры:
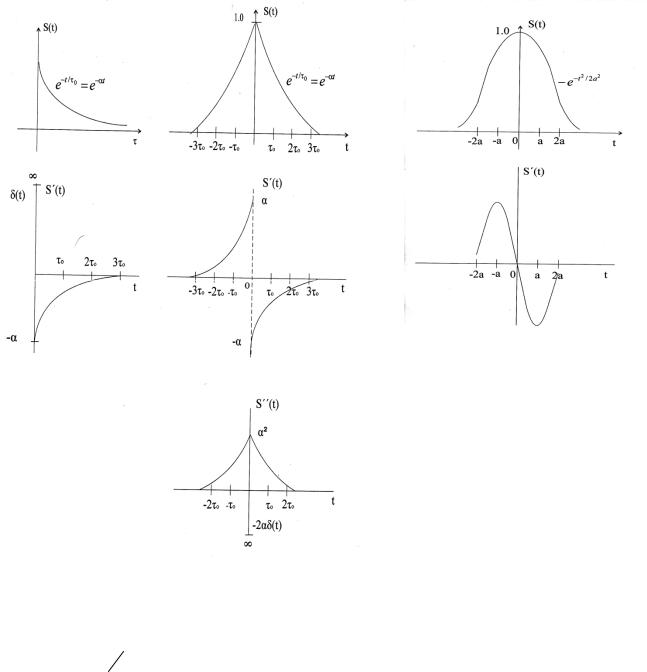
сигнал с разрывом |
сигнал с изломом сигнал без разрыва и излома |
Если S(t) = e−tτ0 = e−ατ , при t ≥ 0 , а при t p 0 S(t)= 0 |
, то |
|||||||||||||||||||
S′(t)=δ(t)−αe−αt ,t ≥ 0 , |
|
|
|
|
|
|
|
|
|
|
||||||||||
SS′(ω)=1−α 1 |
= jω |
|
|
|
|
|
|
|
|
|
|
|||||||||
• |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
α+ jω |
|
α+ jω |
|
|
|
|
ff S (ω)= 1 |
|||||||||||
|
SS (ω)= 1 |
SS′ (ω)= 1 |
|
|
|
|||||||||||||||
|
• |
|
|
|
|
|
|
|
• |
|
|
|
|
|
, а при ω |
α S |
|
|
|
|
Отсюда |
|
|
|
|
|
|
, |
|
|
|
|
|
, что объясняется |
|||||||
|
|
|
|
|
jω |
|
|
α + jω |
|
jω |
||||||||||
наличием функцииδ (t ) в первой производной сигнала S (t). |
||||||||||||||||||||
|
|
−α |
|
|
|
|
|
|
|
|
−αt |
t f |
0 |
|
|
|
||||
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|||||||
Если S(t)= e |
|
|
|
, то |
S′(t)= |
−αt |
при |
0 |
|
|
|
|||||||||
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
αe |
t p |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||

S′(t)не содержит дельта-функции, но терпит в точке t = 0 разрыв S′′(t)отличающийся масштабом и наличием функции - 2αδ(t).
S′′(t)= α2e −α t − 2αδ(t),
• |
|
|
• |
|
|
2α , при ω=0 |
• |
|
|||
SS′′ (ω)=α2 SS (ω)− |
SS′′ (ω)= −α . |
|
|||||||||
|
|
• |
|
|
|
2 |
• |
|
|
|
|
|
|
|
|
|
α |
S(ω)−2α |
|
|
|
||
• |
|
SS′′ (ω) |
|
|
|
|
|||||
SS (ω)= |
|
= |
|
|
|
, отсюда |
|
||||
|
(jω)2 |
|
|
(jω)2 |
|
|
|||||
|
|
|
|
|
|
|
|
||||
• |
|
|
|
|
|
|
|
|
|
• |
|
SS (ω)= |
2α |
(α2 +ω2 ), а при ω |
ff |
SS (ω)= 2α |
, т.е. разрыв первой |
||||||
|
|
|
|
α |
ω2 |
||||||
производной, приводит к убыванию спектра по закону ω12 .
Обобщая данный результат, получим, что вне основной полосы спектр
1
убывает по закону ωn+1 , где n-порядок производной при которой возникает
первый разрыв. Поэтому гауссов сигнал, произведение которого непрерывно для всех значений n до n =∞, должен иметь спектр, скорость которого максимально возможна, что идентично выводу о минимальности произведения f τu для этого сигнала.
Периодическая импульсация спектра вне основной полосы частот, возникает в результате интерференции спектров двух дельта-функций, разнесенных во времени.
Модуляция
Для передачи информации в радиотехнических каналах используются высокочастотные сигналы, параметры которых изменяются по закону несущего информацию управляющего сигнала.
Пусть дан сигнал a(t) = A(t)cos(ω(t)t +ϕ(t)) = A(t)cosψ (t) , изменение
амплитуды сигнала A(t) по закону управляющего сигнала называется амплитудной модуляцией, изменение ψ(t) - угловой модуляцией, причем
изменение ω(t) - частотная модуляция, а изменение ϕ(t)- фазовая модуляция.
Несущая частота ω0 должна быть велика по сравнению с наивысшей частотой спектра узкополосного сигнала Ωmax (ω >> Ωmax ).
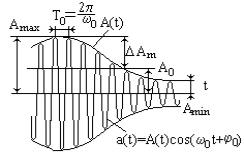
Модулированное колебание имеет спектр, структура которого зависит как от спектра передаваемого сообщения, так и от вида модуляции.
Возможно существование нескольких видов модуляции: непрерывная, импульсная, кодоимпульсная.
Амплитудная модуляция
|
Общее выражение для амплитудно- |
||||
|
модулированного |
колебания |
выглядит |
||
|
следующим образом |
|
|
||
|
|
a(t) = A(t)cos(ω0t + ϕ0 ) |
|||
|
Характер |
огибающей |
A(t) |
определяется |
|
|
видом передаваемого сообщения. |
||||
|
Если |
|
сигнал |
сообщения |
|
s(t) = S0 cos(Ωt + γ ), то |
огибающую модулированного |
колебания можно |
|||
представить в виде |
|
|
|
|
|
A(t) = A0 + ks(t) = A0 + |
Am cos(Ωt + γ ). |
|
|
|
|
Где Ω — частота модуляции, γ коэффициент пропорциональности, амплитуды.
— начальная фаза огибающей, k — Аm=kS0 — абсолютное изменение
Отношение M = Am 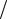 A0 — коэффициент модуляции. Исходя из этого, можно записать:
A0 — коэффициент модуляции. Исходя из этого, можно записать:
A(t)= A0 (1+ M cos(Ωt + γ )).
Тогда амплитудно-модулированное колебание запишется в следующем виде
a(t)= A0 (1 + M cos(Ωt + γ ))cos(ω0t + ϕ0 ).
При неискаженной модуляции (М<1) амплитуда колебания изменяется в пределах от Amin = A0 (1 − M ) до Amax = A0(1+ M).
Максимальному значению соответствует пиковая мощность (при М=1)
Pmax = A02 (1+ M )2 = 4A02 .
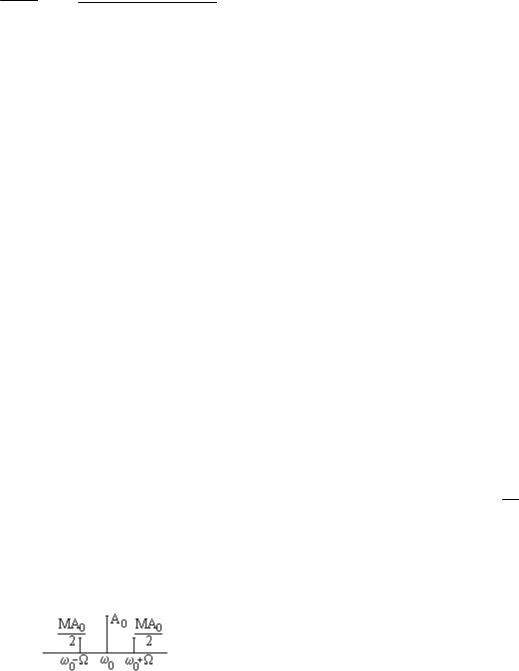
Средняя же за период модуляции мощность (при М=1)
A2 (t)= A02 [1+ M cos(Ωt + γ )]2 = A02 (1+ 0,5M 2 )= 1,5A02 .
Мощность для передачи амплитудно-модулированного сигнала требуется большая, чем для передачи немодулированного сигнала.
Спектр амплитудно-модулированного сигнала
Пусть модулированное колебание определяется выражением
a(t)= A0 (1+ M cos(Ωt + γ ))cos(ω0t +ϕ0 )
Преобразуем это выражение
a(t)= A0 (cos(ω0t + ϕ0 )+ M cos(Ωt + γ )cos(ω0t + ϕ0 ))=
= A0 cos(ω0t + ϕ0 )+ |
M |
cos((ω0 + Ω)t + ϕ0 |
− γ ) . |
|
2 |
||||
|
|
|
Из приведенного выражения видно, что спектр амплитудно-модулированного колебания, при одноканальной модуляции состоит из несущей частоты ω0 и
двух боковых частот (ω0 + Ω) и (ω0 − Ω) , амплитуда которых в M2 раз меньше амплитуды несущей частоты.
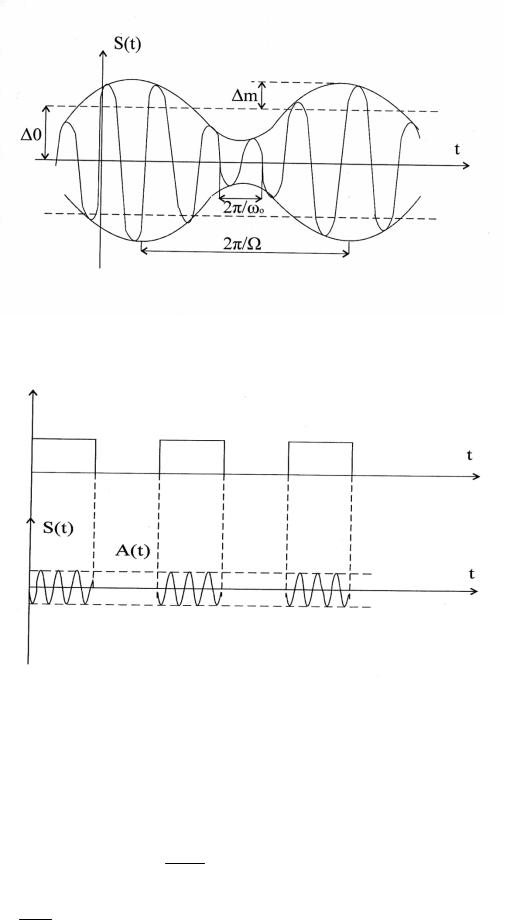
Спектр АМ-колебания
Радиоимпульс
Огибающая для тональной модуляции
A(t) = A0 [1+ M cos(Ωt + γ )], тогда
S(t) = A(t) cos(ω0t + θ0 ) = A0 [cos(ω0t + θ0 ) + M cos(Ωt + γ ) cos(ω0t + θ0 )]=
= A0 cos(ω0t +θ0 ) + MA2 0 cos[(ω0 + Ω)t +θ0 + γ ]+
+ MA2 cos[(ω0 − Ω )t + θ 0 − γ ]
Векторная диаграмма иллюстрирует последнее выражение.
