
Радиотехнические цепи и сигналы
.pdf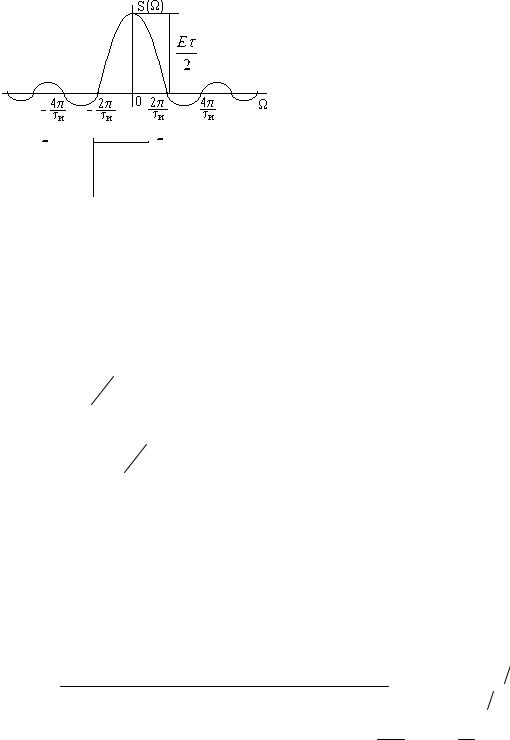
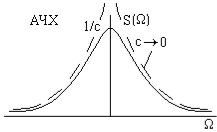
При удлинении (растягивании) импульса расстояние между нулями сокращается, значение S(0) при этом увеличивается. Модуль функции можно рассматривать как АЧХ, а аргумент как ФЧХ спектра прямоугольного импульса. Каждая перемена знака учитывает приращение фазы на π.
При отсчете времени не от середины импульса, а от фронта ФЧХ спектра импульса должна быть дополнена слагаемым Ωτ / 2 , учитывающим сдвиг импульса на время τ / 2 (результирующая ФЧХ показана пунктиром).
S(Ω) = Eτ sin c Ω2τ , Ψ(ω) =0.
Треугольный импульс
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− τ ≤ t ≤ 0 |
||
E |
|
t |
|
|
+ 1 |
, |
||||||||||
|
|
|
|
|
|
|
||||||||||
|
|
|
τ |
|
|
|
|
|
|
|
|
2 |
|
|||
|
|
|
2 |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
S(t) = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
τ |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
E |
|
1 |
− |
|
|
|
|
|
,0 ≤ t ≤ |
|
|||||
|
τ |
|
|
|
2 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
S&(Ω) = E sin c(Ωτ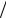 n)(exp( j Ωτ
n)(exp( j Ωτ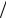 n) − exp(− j Ωτ
n) − exp(− j Ωτ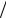 n)) = jΩ
n)) = jΩ
боковых лепестков убывает пропорционально ω12
прямоугольного импульса.
Eτ sin2 Ωτ |
4 |
|
2 |
||
|
|
|
|
|
. Уровень |
|
|
|
|||
2 |
|
Ωτ 4 |
|
|
|
|
|
|
|
||
, а не ω1 , как у
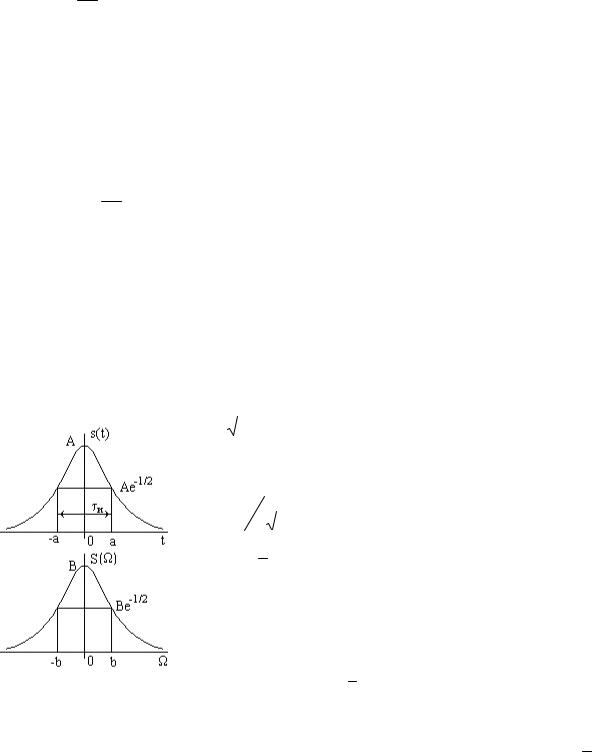
Колоколообразный (гауссовский) импульс
Определяется выражением
− t2
s(t)= Ae 2a2 .
Постоянная а имеет смысл половины длительности импульса, определяемой на уровне е-1/2 от амплитуды импульса. Таким образом, полная длительность
импульса τИ =2a.
Спектральная плотность сигнала
∞ − t2
S&(Ω) = A ∫e 2a2 e− jΩtdt .
−∞
Для удобства дополним показатель степени до квадрата суммы
|
t |
|
|
2 |
|
|
2 |
|
|
|
|
|
||||
− |
|
|
|
|
+ d |
|
− d |
|
|
, |
|
|
|
|||
|
|
|
|
|
|
|
|
|
||||||||
2 |
|
|
|
|
|
|||||||||||
a |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где |
|
величина |
|
|
d |
определяется |
из |
условия |
||||||||
jΩt =2 |
t |
|
|
d |
, откуда |
|
|
|
||||||||
|
|
|
|
|||||||||||||
|
|
|
|
a 2 |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
d = jΩa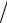

 2 .
2 .
Таким образом, выражение для спектральной плотности можно привести к виду
∞
S&(Ω) = Aed 2 ∫e−(t a
a
 2 +d )2 dt .
2 +d )2 dt .
−∞
Переходя к новой переменной x=(t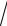 a
a
 2)+d
2)+d

получим
∞
S&(Ω)= Aed 2 ∫e−x2 dx .
−∞
Учитывая, что входящий в это выражение интеграл равен 
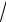 π , окончательно получим
π , окончательно получим
|
|
− |
a2Ωω |
− |
Ωω |
|
S&(Ω)= Aa 2πe |
2 = Be 2b2 , |
|||||
гдеb = 1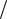 a; B =
a; B = 
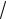 2π aA .
2π aA .
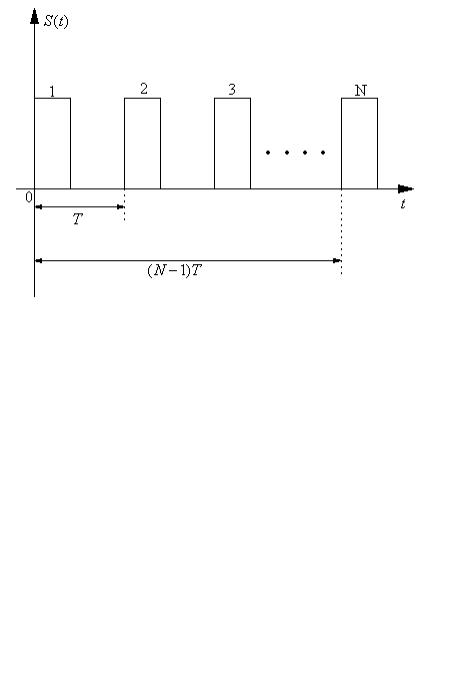
Ширина спектра импульса 2b=2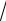 a=2 2τИ =4τИ .
a=2 2τИ =4τИ .
Гауссовский импульс и его спектр выражаются одинаковыми функциями и обладают свойством симметрии. Для него соотношение длительности импульса и полосы пропускания является оптимальным, т. е. при данной длительности импульса гауссовский импульс имеет минимальную полосу пропускания.
Импульс вида sinc(x)
S(t) = sinc(Ωt) = sin(Ωt) |
|
|||||
|
|
|
|
|
Ωt . |
|
|
|
∞ |
|
1 ∞ sin x |
π |
|
|
(ω) = |
∫ |
|
Ω ∫ x |
Ω |
|
S |
|
S(t)dt = |
|
dx = |
|
|
0 |
|
|
|
|
|
|
|
|
−∞ |
|
−∞ |
|
|
Пачка импульсов
S (ω ) = S1 (ω )[1 + exp( − jωT ) + exp( −2 jωT ) + exp( −(N − 1) jωT )].
При ω = |
k 2π |
|
k 2π |
|
|
|
|
|
, где k – целое число exp − |
j |
|
T = 1 |
и |
||
|
|
||||||
|
|
||||||
|
T |
|
|
T |
|
|
|
|
|
|
|
||||
|
k2π |
|
2πn |
, то есть модуль спектральной плотности пачки |
|||
S ω = |
|
|
= NS |
|
|||
|
|||||||
|
T |
|
T |
|
|
|
|
импульсов в точке |
|
2 π n |
в N раз больше модуля спектра одиночного |
||||
|
|
||||||
импульса. |
|
|
|
T |
|
|
|
|
|
|
|
|
|
||
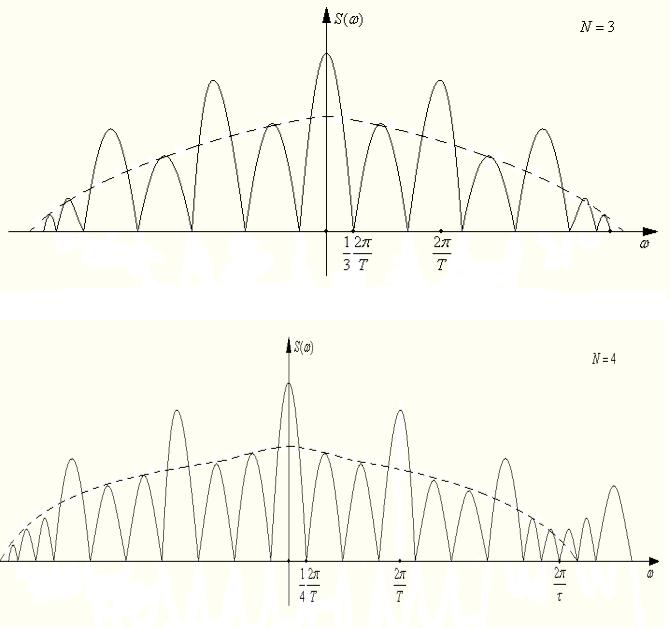
При ω = |
1 |
|
2π |
, S(ω) = 0. |
|
|
|
|
|
||
|
|
||||
|
N |
T |
|
||
При увеличении N спектр расширяется и при N → ∞ принимает линейную структуру периодической функции.
Дельта-импульс (единичный импульс)
Ниже приведены возможные импульсы, площадь которых равна единице:
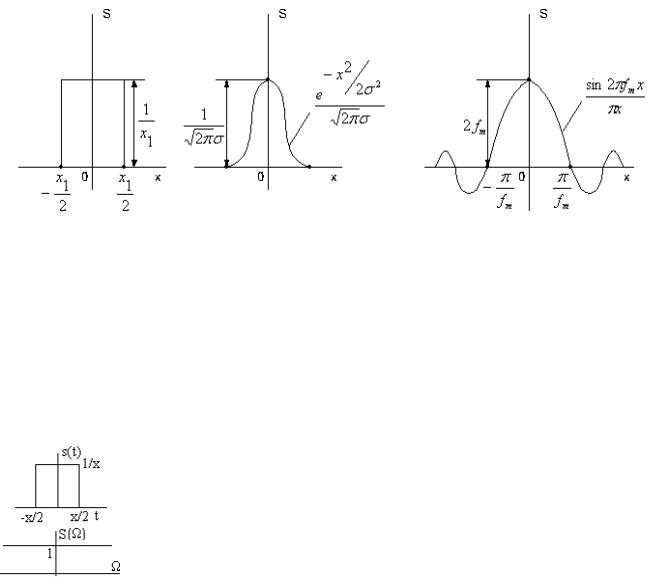
Импульсы, обращающиеся в дельта-функцию при стремлении длительности к нулю.
Амплитуды всех этих импульсов обратно пропорциональны соответствующим образом определенной длительности импульса. При стремлении длительности к нулю амплитуда обращается в бесконечность, а площадь импульса остается неизменной и равной единице.
Сигнал задан соотношением
( ) ∞,при t = 0
δ t = .
0, при t ≠ 0
Ее можно получить из вышеперечисленных импульсов путем устремления τи к нулю.
∞
∫δ (t)dt = 1, следовательно спектр такого сигнала будет постоянным (это есть
−∞
площадь импульса равна единице).
∞ |
∞ |
∫δ(t −t0 )f |
(t)dx = f (t0 )∫δ(t −t0 )f (t)dt = f (t0 ) - стробирующее свойство дельта- |
−∞ |
−∞ |
функции. |
|
Так как по определению функция δ (t − t0 ) равна нулю на всей оси t, кроме
точки t =t0 (где она бесконечно велика), то промежуток интегрирования можно сделать сколь угодно малым, лишь бы он включал в себя точку х0. В
этом промежутке функции f (t) принимает постоянное значение f (t0 ) ,
которое можно вынести за знак интеграла. Таким образом, умножение любой подынтегральной функции f (t) на δ (t − t0 ) позволяет приравнять
интеграл произведения значению f (t ) в точке t =t0
В теории сигналов приходится иметь дело с дельта-функциями от аргументов t или ω, в зависимости от того, в какой области рассматривается функция — во временной или частотной.
Рассмотрим сначала свойства функции δ (t) . В этом случае основное
значение имеет спектральная характеристика дельта-функции. Ранее было установлено, что при сокращении длительности прямоугольного импульса (неизменной амплитуды) ширина основного лепестка спектральной плотности увеличивается, а величина S(0) быстро уменьшается. В данном же случае, когда уменьшение длительности импульса сопровождается одновременным увеличением его амплитуды, значение спектральной плотности остается неизменным и равным величине S(0) = 1 для всех частот. То же самое имеет место при укорочении любого из импульсов. Следовательно, спектральная плотность дельта-функции вещественна и равна единице для всех частот. Из этого также вытекает, что ФЧХ спектра дельта-функции δ (t) равна нулю для всех частот. Это означает, что все
гармонические составляющие единичного импульса при нулевых начальных фазах, суммируясь, образуют пик бесконечно большой величины в момент времени t = 0.
Аналогично функция δ (t − t0 ) , определяющая единичный импульс в
момент t0, имеет спектральную плотность S(ω) = e− jωt0 . Модуль этой функции по-прежнему равен единице, а ФЧХ θ (ω) = −ωt0 .
Найденная ранее спектральная плотность дельта-функции может быть получена и с помощью преобразования Фурье:
S (ω ) = ∞∫ δ (t − t0 )e− jω t dt
− ∞
S (ω ) = e− jω t0 ∞∫ δ (t − t0 )dt = e− jω t0
− ∞
При t0 = 0 S (ω ) = 1. Следует иметь в виду, что правая часть равенства
S (ω ) = 1 является размерной единицей: это площадь импульса, численноравная единице. Если под δ (t) подразумевается импульс напряжения, то
размерность S (ω ) есть вольт на секунда (В*с).
S(Ω)= 1,Ψ(Ω)= 0
Для создания такого импульса необходимы все гармоники.

Экспоненциальный импульс
Сигнал вида s(t)= e−ct , c>0.
Спектр сигнала находится следующим образом
∞ |
∞ |
1 |
|
|
∞ |
|
|
|
|||||
S&(Ω)= ∫e−cte− jΩtdt =∫e−(c+ jΩ)tdt = |
|
e−(c+ jΩ)t |
|
|||
|
|
|
||||
− (c + jΩ) |
||||||
−∞ |
0 |
|
0 |
|||
|
|
|
||||
Запишем сигнал в другой форме
S&(Ω)= |
|
|
1 |
|
|
− jarctg Ω |
|
|
|
|
|
e |
c . |
||
|
|
|
|
||||
c |
2 + Ω2 |
||||||
|
|
|
|
|
= 1
c + jΩ
Если c>0, то e−ct →1(t). Это означает, что мы получим единичный скачек. При
s(t)= lime−ct =1(t)
c→0
получаем следующее выражение для спектра сигнала
S&(Ω)= lim |
1 |
= |
1 |
|
|
jΩ . |
|||
c→0 c + jΩ |
|
|||
Отсюда модуль S(Ω)= Ω1 ,
( ) π 2, при Ω f 0
а фаза Ψ Ω =
−π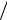 2, при Ω p 0
2, при Ω p 0
Гармонический сигнал
s(t) = A0 cos(ω0 t + θ 0 )
∞
S&(Ω) = ∫cos(ω0t + θ0 )exp(− jΩt)dt = A0π (exp( jθ0 )δ (Ω − ω0 ) + exp(− jθ0 )δ (Ω + ω0 ))
−∞
.
При ω = 0 – постоянное напряжение:
S&(Ω) = A0 2πδ (Ω) .
∞
Если S(t) = A0 + ∑An cos(nΩ1t +θn ) ,
n=1
S&(Ω) = A0 2πδ(Ω) + A1π (exp(jθ1)δ (Ω − Ω1)) + exp(− jθ1)δ (Ω + Ω1) + .
+ A2π (exp( jθ2 )δ (Ω − 2Ω1)) + exp(− jθ2 )δ (Ω + 2Ω1) + ...
Если S(t) = S1(t) + S2 (t) , то:
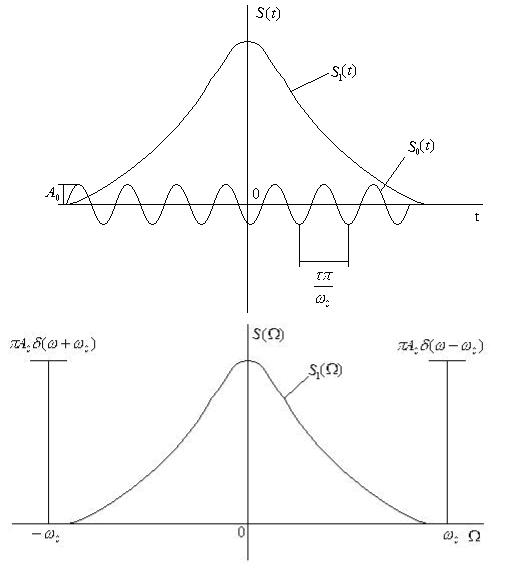
Распределение энергии в спектре непериодического сигнала
|
|
|
∞ |
|
|
|
|
Рассмотрим выражение ∫ f (t)g(t)dt , в котором f(t)=g(t)=s(t). В этом |
|||||||
|
|
|
−∞ |
|
|
|
|
случае данный интеграл равен |
|
|
|
|
|||
∞ s2(t)dt = |
1 |
∞ |
S&(Ω)S&′(Ω)dΩ = |
1 |
∞ S2 |
(Ω)dΩ = Э. |
|
2π |
∫ |
2π |
|||||
∫ |
|
∫ |
|
||||
−∞ |
|
−∞ |
|
|
−∞ |
|
|
Это соотношение носит название равенства Парсеваля.
