Радиотехнические цепи и сигналы
.pdf
где | β |= 2ω Д / Tc = 4πf Д / Tc - скорость линейного изменения частоты внутри импульса. Тогда мгновенное значение колебания, представленного на рис. а, можно записать в виде
βt2
a(t) = A0 cos(∫ω(t)dt) = A0 cos(ω0t + 2 ),−Tc / 2 < t < Tc / 2.
Произведение полной девиации частоты на длительность импульса
2fДTc =m является основным параметром ЛЧМ сигнала. Это так называемая база сигнала. С учетом выкладок, выражение можно записать в форме:
| β |=2πm/Tc2.
При этом сигнал а (t) определяется при β> 0 выражением
a(t) = A cos(ω |
t + |
πmt |
2 |
/ 2 < t < T / 2. |
|
|
),−T |
||||
0 |
0 |
|
T 2 |
c |
c |
|
|
|
|
|
|
|
|
|
c |
|
|
Определим спектральную плотность этого сигнала с помощью общего выражения:
|
Tc / 2 |
|
πmt |
2 |
A |
Tc / 2 |
|
πmt |
2 |
|
|
|
A |
|
|
|
|
|
|
|
|
||||||||
|
∫ |
|
)e− jωt dt = |
∫ |
|
|
|
|
||||||
S(ω) = A0 |
cos(ω0t + |
|
0 |
exp j |
|
|
|
− (ω −ω0 ) |
|
dt + |
0 |
|||
T 2 |
2 |
T 2 |
|
2 |
||||||||||
|
|
|
|
|
|
|
||||||||
|
−Tc / 2 |
|
c |
|
|
−Tc / 2 |
|
|
c |
|
|
|
|
|
Первое слагаемое в правой части полученного выражения определяет всплеск спектральной плотности вблизи частоты ω =ω0 , а второе — всплеск вблизи частоты ω = ω0 .
При определении S(ω ) в области положительных частот второе слагаемое можно отбросить. В первом же слагаемом показатель степени в подынтегральной функции целесообразно дополнить до квадрата разности (β считаем положительной величиной)
πmt2 |
|
πmt2 |
|
|
|
|
|
|
|
|
|
− (ω − ω0 )t + d 2 |
− d 2 = ( |
|
πmt |
− d)2 − d |
2 ,где |
||||||
2 |
− (ω − ω0 )t = |
2 |
|
|
|
|
|||||
Tc |
|||||||||||
Tc |
|
Tc |
|
|
|
|
|
||||
d = (ω − ω0 )Tc / 2
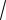πm.
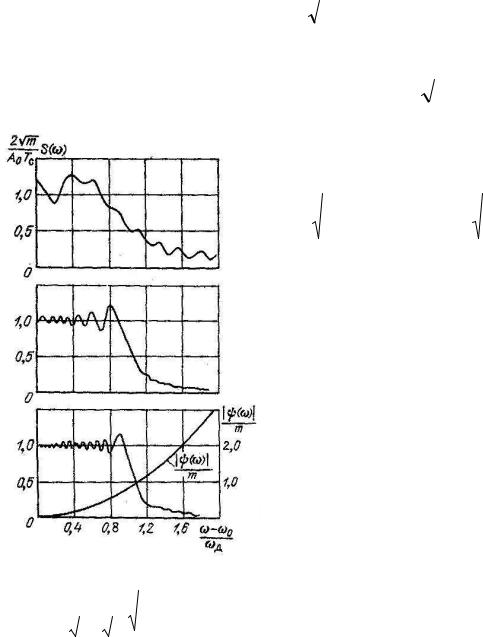
Tc / 2
∫ exp
−Tc / 2
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Переходя к |
новой |
переменной y = |
|
|
πmt /Tc −d, |
|
получаем: |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A0 |
|
|
|
|
|
|
|
Tc |
|
|
|
u1 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S(ω) = |
|
e−id 2 |
|
|
|
|
|
|
∫e jy2 dy, |
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
πm u2 |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где |
|
пределы |
интегрирования |
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
определяются |
выражениями: |
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ω −ω |
|
|
|
|
|
|
|
|
|
|
ω −ω |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
m |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u = |
|
|
|
|
|
1− |
|
|
|
|
0 |
, |
|
u |
= |
|
|
|
1+ |
|
0 |
. |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
2 |
|
|
|
|
|
|
ωД |
|
|
2 |
|
|
|
2 |
|
|
|
|
ωД |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Используем |
известные из математики |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
определения |
|
интегралов Френеля |
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
2 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C(x) = ∫cos |
πy |
|
|
dy, |
S(x) = ∫sinπy |
|
dy, |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
2 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
jzy 2 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
откуда C (x) + iS (x) = ∫e |
|
dy. |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В области положительной частоты имеем |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
АЧХ: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
S(ω) = |
A0 |
Tc |
|
|
1 |
|
|
[C(u1)+C(u2)]2 +[S(u1)+S(u2)]2, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
2 m |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
m |
(ω−ω )2 |
|
S(u )+S(u ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
А ФЧХ: |
θ(ω) =− |
|
|
|
0 |
+arctg |
|
|
|
1 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
4 |
|
ω |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
C(u )+C(u ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
Д |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Из графиков видно, что при увеличении m форма S(ω ) стремится к |
|
|
|
||||||||||||||||||||||||||||||||||||||||||
прямоугольной, а ШС = 2ωД , при этом |
|
θc |
|
|
принимает квадратичный вид |
||||||||||||||||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
(второе слагаемое в θc(ω) стремящееся к π/4опускается). |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
При |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
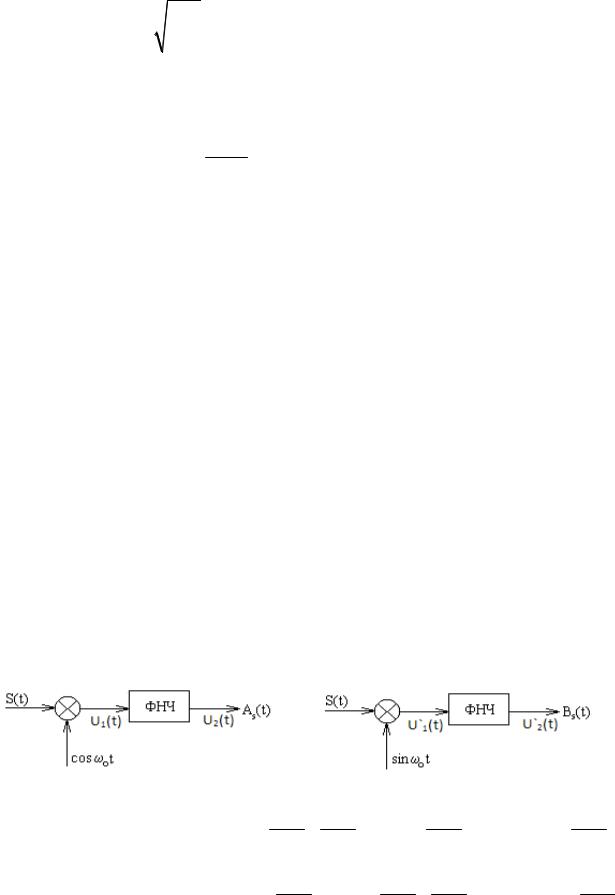
ω = ω |
:U |
1 |
=U |
2 |
= |
π m ,C(U |
) = C(U |
) = 0.5 |
|
0 |
|
|
|
4 |
1 |
2 |
, |
||
|
|
|
|
|
|
|
|
||
S(U1) = S(U2 ) = 0.5 |
|
|
|
||||||
|
|
|
|
||||||
A τ
Вследствие чего S (ω0 ) = 20 0 .
Vm
В области отрицательных частот ФЧХ ЛЧМ сигнала противоположны по знаку. При β <0, то есть при уменьшении с течением времени частоты
заполнения в радиоимпульсе перед правой частью выражение для θc(ω) знак изменяется на обратный.
Узкополосный сигнал
Узкополосный сигнал - это сигнал, у которого полоса частотного спектра значительно меньше несущей частоты:
ω pp 1
ω0 .
S(t) =U(t)cos(ω0t +ϕ(t)) = As (t)cosω0t − Bs (t)sinω0t ,
где U(t) – амплитуда сигнала, Аs(t)=U(t)cos(φ(t)) — синфазная амплитуда, Вs(t)=U(t)sin(φ(t)) — квадратурная амплитуда.
U1(t) = As (t)cos2 ω0t − 12 Bs (t)sin2ω0t = As2(t) + As2(t) cos2ω0t − Bs2(t) sin2ω0t,U1(t) = As2(t)
U1(t) = 12 As (t)sin2 ω0t − 12 Bs (t)cos2ω0t = As2(t)sin2ω0t − Bs2(t) + Bs2(t) cos2ω0t,U2| (t) = Bs2(t)
|
|
|
|
= As (t) + jBs (t) . |
Комплексная амплитуда узкополосного сигнала Us |
||||
|
(t)e |
jω0t |
, |
|
S(t) = Re Us |
|
|
||
|
|
|
|
|
где ejω0t — оператор вращения.
При определении параметров сигнала (амплитуды, частоты и фазы) различными методами можно допустить ошибку.
Например: простейшее колебание s(t)= A0 cosω0t можно представить в форме s(t)= A(t)cosωt , где ω =ω0+ ω . В этом выражении огибающая А(t) в
отличие от Ао является функцией времени, которую можно определить из условия сохранения заданной функции а(t):
|
|
|
A0 cosω0t = A(t)cos(ω0 + |
ω)t , |
|
||
откуда |
|
|
|
|
|
|
|
A(t)= |
A0 cosω0t |
= |
A0 cosω0t |
|
= |
|
A0 |
cos(ω + ω)t |
cos ωt cosω t − sin ωtsinω t |
cos |
ωt − sin ωt tgω t |
||||
0 |
0 |
0 |
|
|
0 |
||
.
Из этого выражения видно, что новая функция А(t) по существу не является “огибающей” в общепринятом смысле, так как она может пересекать кривую а(t) (вместо касания в точках, где А(t) имеет максимальное значение). То есть мы не верно определили огибающую и частоту. Существует метод мгновенной частоты — метод Гильберта для определения частоты.
Для сигнала s(t)= us (t)cos(ω0t + ϕs (t)), найдем
As (t) =Us (t)cosϕs (t),
Bs (t) =Us (t)sinϕs (t).
Тогда параметры сигнала S(t):
Физическая огибающая: Us (t) = 
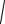As (t)+Bs (t) .
Полная |
|
фаза сигнала |
Ψs (t)= ω0t + ϕs (t), |
а |
мгновенная частота |
|||||||||||||
ωs (t)= ω0 |
+ |
|
dϕs (t) |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
d |
|
|
B (t) |
= ω0 |
+ |
B' (t)A (t)− B (t)A' (t) |
|||||||
|
|
|
ωs (t)= ω0 + dt arctg |
|
A (t) |
S |
A2 (t)+ B2 |
(t) |
S |
|
||||||||
|
|
|
|
|
|
|
|
|
S |
|
|
|
S |
S |
|
|||
|
|
|
|
|
|
|
|
|
S |
|
|
|
S |
S |
|
|
|
|
|
|
|
|
|
|
|
jω0t |
|
|
|
|
|
|
|
|
|
|
|
|
|
& |
|
], где Us (t) - комплексная огибающая |
||||||||||||||
Заметим, что s(t)= Re[us (t)e |
|
|||||||||||||||||
сигнала.
Свойства комплексной огибающей:
1)Модуль комплексной огибающей равен физической огибающей и постоянен, не зависит от выбора частоты.
2)Модуль сигнала s(t) всегда меньше или равен us(t). Равенство
наступает тогда, когда cos ωot = 1. В эти моменты производная сигнала и производная огибающей равны.
3)Физическая огибающая совпадает с максимальным значением амплитуды сигнала.
Обозначим временные функции и соответствующие им спектры как:
|
& |
(ω), |
& |
|
|
& |
|
|
|
|
|
|
|
|
|
|
|
причем |
s(t)→ S |
us |
(t)→ Gs (ω), |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
∞ |
& |
|
|
jω0t |
− jωt 1 |
∞ |
& |
− j(ω −ω0 )t |
|
1 |
∞ |
|
& |
|
j(ω +ω0 )t |
|
|
S(ω)= |
∫ |
Re[US (t)e ]e dt = |
2 |
∫ |
US (t)e |
|
dt + |
2 |
∫ |
US |
(t)e |
|
dt = |
|||||
|
|
|
|
|
|
|
||||||||||||
|
−∞ |
|
|
|
|
|
−∞ |
|
|
|
|
−∞ |
|
|
|
|
||
1 & |
(ω − ω0 )+ |
1 & |
(ω + ω0 ) |
|
|
|
|
|
|
|
|
|
|
|
|
|||
= 2 GS |
2 GS |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
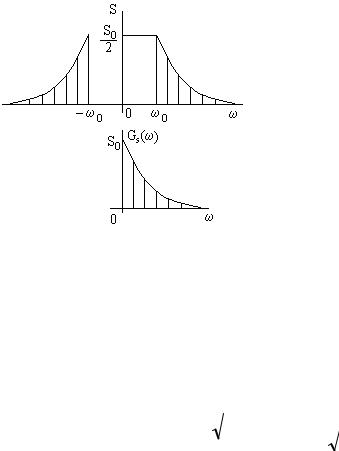
Зная комплексную огибающую, можно найти ее спектр, а затем и сам сигнал:
S |
0 |
|
( |
|
0 ) |
|
|
|
|
|
−b ω −ω |
|
, |
ω f ω0 , тогда |
|||
пусть S&(ω)= |
|
e |
|
|
|
|||
2 |
|
|
|
|||||
|
|
|
|
0, |
ω |
p |
ω0 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
& |
(ω)= |
S0e−bω , ω f 0 |
. |
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
GS |
|
|
0, ω p 0 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Зная Gs (ω) найдем Us (ω) . |
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
& |
(t) |
|
|
|
S0 |
|
∞ |
|
−bω |
|
|
jωt |
|
|
|
S0 |
∞ |
|
−ω(b− jt ) |
|
S0 |
|
||||||||
|
|
|
|
|
|
|
|
US |
= |
|
|
|
|
|
|
|
∫ |
e |
|
|
|
e |
|
dω |
= |
|
∫ |
e |
|
dω = |
|
|
||||||
|
|
|
|
|
|
|
|
2π |
|
|
|
|
|
2π |
|
2π (jt |
− b) |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−∞ |
|
|
|
|
|
|
|
|
|
|
−∞ |
|
|
|
|
||
Помножим на (-b-jt) и получим вещественную и мнимую части |
|
|||||||||||||||||||||||||||||||||||||
соответственно A |
= |
S0 |
|
|
b |
, |
B |
|
|
= |
|
S0 |
|
|
|
t |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
||||||||
2π b2 + t2 |
|
|
|
2π b2 + t2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
S |
|
|
S |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
Отсюда амплитуда US (t)= |
|
|
|
|
|
S0 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
AS2 + BS2 |
|
|
= |
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
2π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
b2 + t2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Аналитический сигнал
Пусть есть сигнал s(t), определяемый как
s(t)= |
1 |
∞ S&(ω)ejωtdω . |
|
|
|
|
|
2π |
|
|
|
|
|||
|
|
∫ |
|
|
|
|
|
|
|
|
−∞ |
|
|
|
|
Разделим его на две составляющие |
|||||||
s(t)= |
|
1 |
0 S&(ω)ejωtdω + |
1 |
∞ S&(ω)ejωtdω . |
||
|
2π |
2π |
|||||
|
|
∫ |
∫ |
|
|||
|
|
|
−∞ |
|
0 |
|
|
|
|
|
|
|
|
π |
∫ |
В этом выражении zS (t)= |
1 |
∞ S&(ω)e jωtdω –– аналитический сигнал. |
|||||
|
|||||||
|
|
|
|
|
|
|
0 |
Если |
|
|
|
|
ввести |
|
|
переменную ξ = −ω |
|
|
|
|||||||||||
|
1 |
0 |
& |
jωt |
|
|
1 |
0 |
& |
|
− jξt |
|
1 |
∞ |
& |
|
− jξt |
|
1 |
& |
|
|
|
2π |
∫ |
S (ω )e |
|
dω = − |
2π |
∫ |
|
(− ξ )e |
|
dξ = 2π |
∫ |
|
(− ξ )e |
|
dξ = |
|
(t) |
||||
|
|
S |
|
S |
|
2 zS |
||||||||||||||||
|
|
− ∞ |
|
|
|
|
|
|
− ∞ |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
То есть: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
s(t)= zS (t)+ zS (t) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
& |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Реальный |
сигнал |
s(t)= Re[zS (t)], |
сигнал, |
|
сопряженный |
|
по |
|||||||||||||||
|
sˆ(t)= Im[zS (t)]. Аналитический сигнал есть zS (t)= s(t)+ sˆ(t). |
|
|
|||||||||||||||||||
то
.
Гильберту
ˆ |
1 ∞ |
s(τ ) |
dτ , |
s(t)= |
1 |
∞ sˆ(τ ) |
|
|||
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
dτ |
–– прямое и обратное преобразование |
||||
s(t)= − |
π |
∫ |
τ − t |
π |
∫ |
|||||
|
|
|
τ − t |
|
||||||
|
|
−∞ |
|
|
|
|
−∞ |
|
|
|
Гильберта.
Определение несущей и огибающей по методу Гильберта
Использование сигнала, сопряженному по Гильберту позволяет однозначно определять параметры узкополосного сигнала:
Амплитуда сигнала US (t)=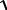 
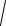s2 (t)+ sˆ2 (t), фаза ϕ(t)= arctg sˆ(t)
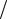s(t). Значение
мгновенной частоты ω(t)= |
dϕ(t) |
= |
s(t)sˆ(t)− s' (t)sˆ(t) |
. |
||||||
dt |
|
|||||||||
|
|
|
|
|
|
|
s2 (t)+ sˆ2 (t) |
|
|
|
Пример: s(t)= cosω0t . |
|
|
|
|
||||||
sˆ(t)= − |
1 |
∞ cosω τ |
1 |
∞ cosω |
(x + t) |
|
|
|||
|
∫ |
0 dτ = − |
|
∫ |
0 |
dx = sin |
ω0t . |
|||
π |
π |
|
||||||||
|
τ − t |
x |
|
|
||||||
|
|
−∞ |
|
|
−∞ |
|
|
|
|
|
US (t)= 
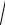cos2 ω0t + sin2 ω0t = 1 –– точное определение огибающей.
Любой сигнал можно разложить в ряд Фурье: s(t)= ∑(an cosωnt + bn sinωnt).
Сопряженный по Гильберту сигнал: sˆ(t)= ∑(an cosωnt − bn sinωnt).
Если сигнал представлен не рядом Фурье, а интегралом Фурье, то справедливы следующие соотношения
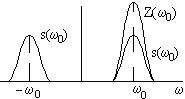
s(t)= |
1 |
|
∞ |
[Acos ωt + B sin ωt]dω , |
||
|
π |
∫ |
||||
|
|
|
||||
|
|
|
|
0 |
|
|
sˆ(t)= |
1 |
|
∞ |
[Acosωt − Bsinωt]dω . |
||
π |
∫ |
|||||
|
|
|||||
|
|
|
|
0 |
|
|
|
|
|
|
|
Свойства аналитического сигнала |
|
1. Спектр аналитического сигнала содержит только положительные частоты
( ) 0; ω p 0
Z ω =
2Sa (ω ); ω f 0
2. Произведение аналитического сигнала zs(t) на сопряженный ему сигнал zs*(t) равно квадрату огибающей исходного (физического) сигнала s(t).
zS (t)z&S (t)= us2 (t)= [s(t)+ jsˆ(t)][s(t)− jsˆ(t)]
3.Спектральная плотность комплексной огибающей u&S (t)совпадает со
смещенной |
на |
величину |
ω0 |
влево |
спектральной |
плотностью |
||||||
аналитического сигнала zs(t). |
|
|
|
|
|
|
|
|
|
|||
∞ |
|
∞ |
|
|
|
|
|
∞ |
|
|
|
(ω − ω0 ) |
Z(ω)= ∫zS (t)e |
− jωt |
& |
(t)e |
− jω0t |
e |
− jωt |
& |
(t)e |
− j(ω −ω0 )t |
& |
||
|
dt = ∫uS |
|
|
|
dt = ∫uS |
|
dt = GS |
|||||
−∞ |
|
−∞ |
|
|
|
|
|
−∞ |
|
|
|
|
Иначе Z(ω0 − Ω)= G& (Ω)= 2s&(ω0 + Ω), где Ω = ω − ω0 .
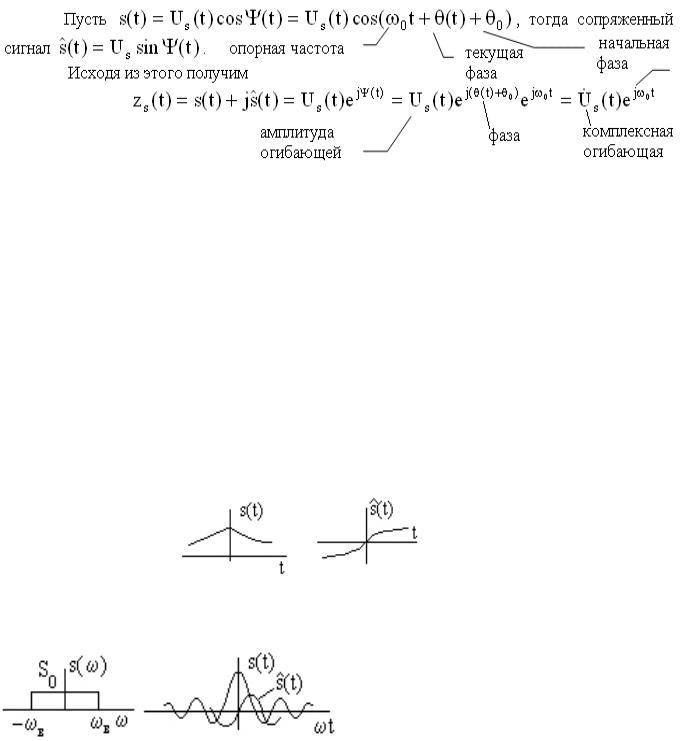
Преобразование Гильберта для узкополосного процесса
Свойства преобразований Гильберта
sˆ(t)= H(s(t)) ––преобразование Гильберта, где Н( ) – оператор преобразования.
1.H[a1s1(t)+ a2s2 (t)]= a1H[s1(t)]+ a2H[s2 (t)]
2.H[const]= 0
3.Если исходный сигнал s(t) имеет экстремум в какой-то точке, то в окрестности этой точки функция sˆ(t)проходит через ноль.
Пример. Сигнал s(t) – идеальный низкочастотный сигнал.
z |
(t)= |
S0 |
ωEe jωtdω = |
S0 |
|
[e jωE t −1] |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
S |
|
π ∫ |
|
|
πjt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
S |
0 |
|
|
|
|
|
|
S |
0 |
sinω |
E |
|
|
|
|
s(t)= Re[z |
|
(t)]= Re |
|
|
[cosω |
|
t + jsinω |
|
t −1] |
= |
|
|
sin cω |
|
t |
||||||||
S |
|
|
|
E |
E |
|
|
|
|
E |
|||||||||||||
|
|
|
|
|
|
|
πjt |
|
|
|
|
|
|
π |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Частотные и временные характеристики радиотехнических цепей
Пусть имеется линейный активный четырехполюсник.
|
|
& |
|
|
|
|
& |
U2 |
|
jϕ(ω ) |
|
1. Передаточная функция |
K(ω)= |
& |
= K(ω)e |
|
, характеризует изменение |
|
|
U1 |
|
|
|
сигнала на выходе относительно сигнала на входе. Модуль K(ω)называют амплитудно-частотной характеристикой или просто амплитудной характеристикой. Аргумент ϕ(ω) –– фазо-частотной характеристикой или просто фазовой.
|
|
1 |
∞ |
& |
jωt |
|
2. Импульсная характеристика |
g(t)= |
2π |
∫K(ω)e |
|
dω –– реакция цепи на |
|
|
|
|
−∞ |
|
|
|
единичный импульс. Характеризует изменение сигнала во времени. Связь с
передаточной |
функцией осуществляется |
через обратное и |
прямое |
|||
|
|
|
∞ |
|
|
|
преобразование |
Фурье (соответственно) |
& |
|
jωt |
dt . Или |
же через |
K(ω)= ∫g(t)e |
|
|||||
−∞
∞
преобразование Лапласа K(p)= ∫g(t)e− ptdt .
0
t
3. Переходная функция h(t)= ∫g(t)dt –– реакция цепи на единичный скачек.
0
Апериодический усилитель
Схема замещения простейшего апериодического усилителя. Усилительный прибор представлен в виде источника тока SE1 с внутренней проводимостью Gi=1/Ri. Емкость С включает в себя межэлектродную емкость активного элемента и емкость внешней цепи, шунтирующей нагрузочный резистор Rн.