Кафедра геометрии, СГУ, Мех-мат. Новиков В.Е.

Глава 2. Аналитический метод изучения фигур

1. Системы координат

Аналитический метод решения задач геометрии иногда называют методом координат, суть его состоит в некотором взаимно однозначном переходе от точек изучаемого пространства к их координатам и обратно. На этом пути сначала вспомним, что является линейным пространством.

Определение 1. Алгебраическая система на множестве V, с внутренней бинарной операцией (сложение) и внешней операцией (умножение на элементы некоторого поля k) называется линейным пространством V над k, если для этих операций выполняются свойства:

9.a + b = b + a (коммутативность сложения);

10.a +( b + c ) = ( a + b )+ c (ассоциативность сложения);

11.a + 0 = 0 + a = a (существование нуля);

12.a + (– a ) = (– a ) + a = 0 (существование противоположного элемента);

13.( a ) = ( ) a (ассоциативность умножения на скаляры);

14.( + ) a = a + a (дистрибутивность сложения скаляров относительно умножения);

15.( a + b ) = a + b (дистрибутивность сложения векторов относительно умножения);

16.1 a = a .

Где a , b , c , 0 ,(– a ) V; , ,1 k. При этом элементы базисного множества V линейного пространства часто называют векторами, а элементы поля k — скалярами.

ПРИМЕРЫ. 1. Пространство Vect(i), i=1, 2, 3, векторов на прямой, на плоскости, в пространстве.

2. kn = {(a1, a2, …, an) | ai k, 1 i n} — координатное линейное пространство над произ-

вольным полем k. Операции: если k, a, b kn, т.е. a = (a1, a2, …, an), b = (b1, b2, …, bn), то a + b := (a1 + b1, a2 + b2 , …, an + bn),

a := ( a1, a2, …, an).

В частности само поле k = k1 является линейным пространством над самим собой.

3. Пространство M(R,R) всех вещественных функций на числовой прямой с естественными операциями сложения и умножения на число:

Если f(x), g(x) M(R,R), R, то (f + g)(x) := f(x) + g(x),

( f)(x) := (f(x)), для всех x R.

4. Пространство C(R,R) всех непрерывных вещественных функций на R. Это следует из того, что сумма непрерывных функций и произведение непрерывной функции на число являются непрерывными функциями. А также пространство C([0,1],R) всех непрерывных вещественных

функций на [0,1]. Ясно, что C(R,R) C([0,1],R).

5.По аналогичной причине линейным вещественным пространством является множество D(R,R) всех дифференцируемых вещественных функций на R.

6.Линейными вещественными пространствами являются множество P(R) всех многочленов от одной вещественной переменной x с вещественными коэффициентами и его подмножество

Pn(R), состоящее из всех многочленной степени n.

Ясно, что имеют место включения: Pn(R) P(R) D(R,R) C(R,R) M(R,R). Определение 2. Пусть V — вещественное линейное пространство. Отображение вида :

V V R, обозначаемое ( a , b ):= ( a , b ), называется скалярным произведением на простран-

стве V, если оно удовлетворяет следующим свойствам:

1)( a , a ) 0, причем ( a , a ) = 0 тогда и только тогда, когда a = 0 (положительная оп-

ределенность);

2)( a , b ) = ( b , a ) (симметричность);

3)( a + b , c ) = ( a , c ) + ( b , c ) (аддитивность по первому аргументу);

14

Кафедра геометрии, СГУ, Мех-мат. Новиков В.Е.

4) ( a , b ) = ( a , b ) (однородность по первому аргументу).

ЗАМЕЧАНИЕ. Свойства 3) и 4) называют линейностью по первому аргументу скалярного произведения. Оно означает, что скалярное произведение от линейной комбинации равно линейной комбинации скалярных произведений с теми же коэффициентами соответственно. Учитывая свойство 2) легко показать, что скалярное произведение линейно и по второму аргументу. Такие функции называют билинейными. Таким образом, скалярное произведение –

это положительно определенный симметрический билинейный функционал : V V R.

Например: 1. ( a , b ) := | a || b |cos ab — скалярное произведение, определяемое на основании метрики, имеющейся на прямой, на плоскости и в пространстве (Vect(i), i = 1, 2, 3).

2. (a, b) := a1b1 + a2b2 + … + anbn — пример скалярного произведения в n-мерном арифметическом пространстве kn = {(a1, a2, …, an) | ai k, 1 i n}.

1

3. (f, g) := f (t)g(t)dt — скалярное произведение в пространстве C([0,1],R).

0

4. (a, b) := a1b1 + a2b2 + … + aibi + … — скалярное произведение в гильбертовом пространстве l2. Элементами этого пространства являются бесконечные последовательности вещественных

числа в этом пространстве определяются покоординатно, как в Rn.

Определение 3. Вещественное линейное пространство V с заданным на нем скалярным произведением называется евклидовым пространством.

Однако, для построения геометрии недостаточно только линейного пространства, т.е. пространства векторов, необходимо ввести еще одно множество однотипных объектов — это множество точек. В силу чего имеем следующее определение.

Определение 4. Аффинным (или точечно-аффинным) пространством над векторным про-

странством V называется множество A, элементы которого называются точками, вместе с ото-

бражением A A V, сопоставляющим любым двум точкам A, B A, некоторый вектор AB V (векторсначаломвA иконцомB) иудовлетворяющимследующимаксиомам:

1)Для любой точки A A и любого вектора a V существует единственная точка B A,

такая, что AB = a (аксиома откладывания вектора);

2)Для любых точек A, B, C A : AB + BC = AC (аксиома суммы).

При этом линейное пространство V называется ассоциированным с аффинным пространством A или линеалом пространства A. Его размерность dimV называется размерностью аффинного пространства и обозначается dim A.

Аффинное пространство над евклидовым пространством называется точечно-

евклидовым или просто евклидовым.

Например: 1. Прямая, плоскость и пространство являются аффинными пространствами над векторными пространствами Vect(1), Vect(2), Vect(3) соответственно.

2. Всякое векторное пространство V превращается в аффинное пространство над самим собой,

если мы определим отображение V V V, следующимобразом: ab = a – b.

Определение 5. Пусть в аффинном пространстве A над V зафиксирована точка O, которую будемназыватьначаломилиполюсом.

1. Векторная система координат с данным полюсом O — это взаимно однозначное отображение : A V, которое ставит в соответствие каждой точке M ее радиус-вектор, т.е. вектор

OM , определяемый началом в точке O и концом в точке M .

2. Пусть дополнительно зафиксирован базис e= (ei ) пространства V. В этом случае говорят, что

задан репер Oe. Аффинная система координат с данным полюсом O и базисом e ставит в соответствие каждой точке M координатную строку (столбец) радиус-вектора данной точки относительно выбранных полюса и базиса. Координаты радиус-вектора точки M в базисе e называются аффинными координатами точки M относительно репера Oe. Данную аффинную

15

Кафедра геометрии, СГУ, Мех-мат. Новиков В.Е.

систему координат будем обозначать также Oe.

3. Аффинная система координат в евклидовом пространстве с ортонормированным базисом называется декартовой или прямоугольной.

В общем случае всякое взаимно однозначное отображение : A K в координатное множество K называется системой координат на аффинном пространстве A. Если pr1( ) A

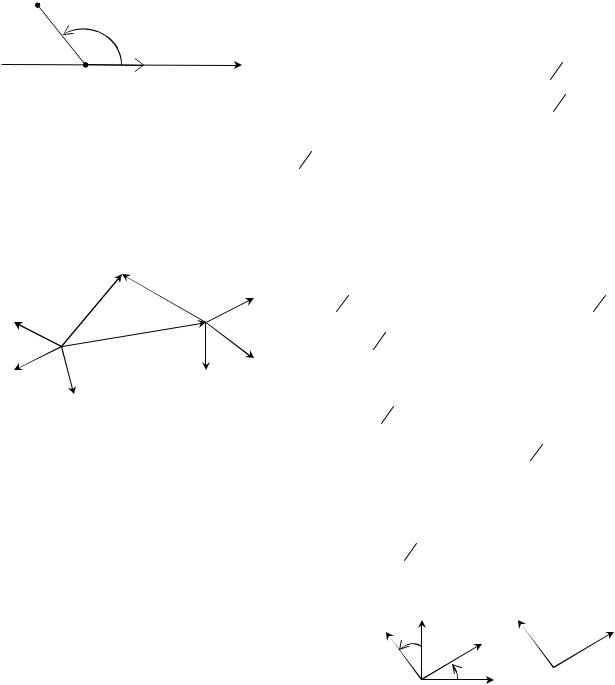
(pr1( ) A), то система называется частичной. Если pr1( ) = A, то система координат называется полной. Например, векторная система координат является полной. Полярная система координат с полярным полюсом O и полярной осью l (см. рис. 1) на плоскости ставит в соответствие каждой точке M : 1) расстояние r (полярный радиус) от точки M до начала O; 2) угол

наклона (полярный угол) радиус-вектора точки M к полярной оси l, относительно выбранно-

Например:

1. Формулы преобразования аффинных координат точки в пространстве:

16

Кафедра геометрии, СГУ, Мех-мат. Новиков В.Е.

2.Основные формулы аналитической геометрии.

Пусть относительно некоторой декартовой системы координат в пространстве известны

координаты точек A(xA , y A , z A ) , B(xB , yB , zB ) , C(xC , yC , zC ) , D(xD , yD , zD ) . Тогда справедливы следующие формулы:

1. Координаты вектора AB(xB xA , yB y A , zB z A ) . (1)

Действительно, AB = rB rA (см. рис. 4), откуда по теореме 1.6 (о координатах линейной комбинации векторов) следует формула 1.

2. Длина отрезка | AB | (xB xA )2 ( yB y A )2 (zB z A )2 . (2)

Действительно, по определению | AB | AB2 , откуда учитывая вычисление скалярного произведения в декартовой системе координат (см. гл. 1) получим формулу 2.

3. Деление отрезка в данном отношении. Точка C делит отрезок AB в отношении CBAC ,

Действительно, по применению векторного произведения S = 12 | [AB, AC] | , что в декарто-

вых координатах дает формулу (5a). Формула на плоскости следует из (5a), если положить все третьи координаты равные нулю, т.е. z A = zB = zC = 0.

ЗАМЕЧАНИЕ. Последнюю формулу иногда записывают иначе:

Действительно, если в данном определителе вычтем первую строку от второй и третьей, а полученный определитель разложим по последнему столбцу, то получим (5b).

17

Кафедра геометрии, СГУ, Мех-мат. Новиков В.Е.

Доказательство. По применению смешанного произведения векторов имеем Vтетраэдра = = 16 | AB AC AD|, что в декартовых координатах дает первую формулу 6.

ЗАМЕЧАНИЕ. Формулу 6 также можно записать в следующем виде:

Достаточно первую строку этого определителя вычесть от второй, третьей и четвертой, а полученный определитель разложим по последнему столбцу, чтобы получить (6).

3. Уравнения фигур.

Определение 6. Понятие фигура подразумевает некоторое произвольное подмножество точек плоскости или пространства. Поэтому с каждым уравнением (x, y, z) 0 связана неко-

торая фигура , координаты точек которой являются решением этого уравнения:

A (xA , y A , z A ) 0 .

Сама фигура называется графиком уравнения (x, y, z) 0 или фигурой, определяемой данным уравнением. Уравнение (x, y, z) 0 называется уравнением фигуры относительно заданной системы координат.

В уравнении фигуры могут присутствовать параметры (x, y, z,t1,t2 ,...,ts ) 0 , т.е. фигура может быть задана «по частям». При каждом наборе значений t1,t2 ,...,ts имеем уравнение(x, y, z,t1,t2 ,...,ts ) 0 части этой фигуры.

Свойства уравнений фигур, связанные с теоретико-множественными операциями

Пусть 1 (x, y, z) 0 и 2 (x, y, z) 0 уравнения фигур 1 и 2 соответственно.

1 . Фигура 1 является частью фигуры 2, тогда и только тогда, когда уравнение фигуры 2 является следствием уравнения фигуры 1:

( 1 (x, y, z) 0 2 (x, y, z) 0 ) ( 1 2).

2 . Фигуры совпадают тогда и только тогда, когда их уравнения равносильны, то есть

4 . Совокупность уравнений или произведение уравнений некоторых фигур определяет объединение этих фигур:

( = 1 2).

18