Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Саратовский государственный университет им. Н.Г. Чернышевского

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Lektsii_po_analiticheskoy_geometrii_Novikov.pdf

Скачиваний:

110

Добавлен:

09.06.2015

Размер:

853.56 Кб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 910 / 1210 11 12 > Следующая >>>

		Кафедра геометрии, СГУ, Мех-мат. Новиков В.Е.
ными инвариантами. Можно показать (самостоятельно), что 1, 2 всегда являются действи-
тельными числами.
Учитывая теоремы 4.2 и 4.1 получаем следующее правило классификации фигур -го
порядка на плоскости:
	> 0	= 0	< 0
	Линия эллиптического типа	Линия параболического типа	Линия гиперболического типа
0	ЭЛЛИПС	ПАРАБОЛА	ГИПЕРБОЛА
Линия не	1) Если знаки 1 и 2 сов-
распадается	падают со знаком —
	мнимый эллипс;
	2) Если знаки 1 и 2 про-
	тивоположны знаку —
	действительный эллипс.
= 0	ТОЧКА(пара мнимых	ПАРА параллельных пря-	ПАРА пересекающих-
Линия рас-	прямых, пересекающихся	мых	ся прямых
падается на	в действительной точке)	1) a22 – a22a > 0 — прямые
пару прямых		1) a22 – a22a > 0 — прямые
		действительные и различные;
		2) a22 – a22a = 0 — прямые
		совпадают;
		3) a22 – a22a < 0 — прямые
		мнимые.

Эллипс, гипербола и парабола

Будем решать следующую задачу:

Пусть зафиксирована точка F и прямая l. Найти геометрическое место точек M, для кото-

рых отношение расстояний от M до точки F и до l прямой является постоянным:

(M , F)

const := e > 0.

(M ,l)

Случай 1, если e = 1. Обозначим (F, l) = p, и выберем систему координат, в которой

, 0), l: x = –

(см. рис.1).

M(x, y)

(M, F) = |

| = |(x –

, y)| =

y2 .

(M, l) = |x

(M , F)

(

)2 y2

|x +

| ) = 1. Откуда

(M ,l)

Рис. 1

p 2

( x–

)

= ( x+

)

, тогда

– px

+ y

+ px+

, сле-

довательно,

y2 = 2px

получаем уравнение параболы.

o F называется фокусом параболы;

l называется ее директрисой;

o p называется фокальным параметром или просто параметром

параболы. Число

на-

зывается фокальным расстоянием.

Случай 2, если e < 1. Обозначим (F, l) = d. В этом случае ( 1e – e) > 0, поэтому существу-

Кафедра геометрии, СГУ, Мех-мат. Новиков В.Е.

ет a > 0, такое что

d = a( 1 – e) . Выберем систему координат, в которой F(ae, 0),

l : x = a .

(M, F) = |

| = |(x – ae, y)| =

(x ae)2 y2 .

(0, b)

M(x,y)

l: x= e

(M, l) = |x –

e |.

(M , F)

= (

(x ae)2

|x –

|) = e. Откуда

(a,0)

(M ,l)

(x – ae)

+ y

= e

(x – e )

тогда x

–2aex + a e

+ y

= e x

–

2 a2

Рис. 2

2 e

x e

+ e

e2 , следовательно,

(1– e ) + y

= a (1– e ). Делим обе части на a (1– e ):

=1. Так как a (1– e ) > 0,

a2 (1 e2 )

то полагая

= a

(1– e ) имеем

уравнение эллипса.

F( ae, 0) называются правым и левым фокусами эллипса;

l : x = ae

называются правой и левой директрисами эллипса;

e =

называется (числовым) эксцентриситетом;

1 a2

c =

a2 b2

называется линейным эксцентриситетом, c = ae.

o Число 2c называется фокусным расстоянием, число p = b2 — фокусным параметром a

или просто параметром. Числа a и b называются соответственно большой и малой полуосью. Точка (0,0) называется центром, точки ( a,0) и (0, b) называются вершина-

ми эллипса. Расстояние (M, F) называется фокальным расстоянием точки M.

Случай 3, если e > 1. Обозначим (F, l) = d. В этом случае (e – 1e ) > 0, поэтому существу-

l: x=

ет a > 0, такое что

d = a(e – 1 ) . Выберем систему ко-

(0, b)

M(x, y)

ординат, в которой

F(ae, 0), l : x = e . Полностью

повторив дальнейшие рассуждения случая 2, получим:

= 1. Так как a2(1 – e2) < 0, то a2(e2 – 1)

(a, 0) F(ae,0)

a2 (1 e2 )

= – a2(1 – e2) > 0. Полагая b2 = a2(e2 – 1) ,

Рис. 3

имеем

–

уравнение гиперболы.

F( ae, 0)

называются правым и левым

фокусами гиперболы;

l : x = ae

называются правой и левой директрисами гиперболы;

	Кафедра геометрии, СГУ, Мех-мат. Новиков В.Е.
b2
o e = 1 a2	называется (числовым) эксцентриситетом;

o c = a2 b2 называется линейным эксцентриситетом, c = ae.

o Число 2c называется фокусным расстоянием, число p = b2 — фокусным параметром a

или просто параметром. Число a называется действительной полуосью, b называется мнимой полуосью. Точка (0,0) называется центром, точки ( a,0) называются вершинами гиперболы. Расстояние (M, F) называется фокальным расстоянием точки M. Пря-

мые ax by = 0 называются аси́мптотами.

Итак, справедлива следующая теорема.

ТЕОРЕМА 4.3 (Директориальное свойство эллипса, гиперболы и параболы – общее свойство конических сечений). Для любой точки эллипса, гиперболы и параболы отношение ее фокального расстояния до соответствующей директрисы есть величина постоянная, равная эксцен-

триситету. (Доказательство самостоятельно)

ТЕОРЕМА 4.4 (Фокальное свойство эллипса). Для любой точки эллипса сумма ее фокальных расстояний постоянна, а именно

(M, F1) + (M, F2) = 2a,

где F1(– ae, 0), F2(ae, 0).

Доказательство. (M,F1,2) = |M,F1,2| = |(x ae, y)| = (x ae)2

= x2 2ae a2e2 y2 .

x2b2

Так как M(x, y) точка эллипса, то

= 1, откуда y

= b –

. Подставим b

= a

(1– e ),

получим y2 = a2(1 – e2) – x2(1 – e2). Подставляя в предыдущее выражение, получим:

(M, F1,2) = x2 2ae a2e2 a2 a2e2 x2 x2e2 = a2 2aex x2e2 = (a xe)2 .

(M, F1) + (M, F1) = (a xe)2 + (a xe)2 = |a + xe| + |a – xe|. Так как e < 1 и | x | a, то мо-

дуль можно опустить, получим (M, F1) + (M, F1) = a + xe + a – xe = 2a.

ТЕОРЕМА 4.5 (Фокальное свойство гиперболы). Для любой точки гиперболы модуль разности ее фокальных расстояний постоянен, а именно

| (M, F1) – (M, F2)| = 2a, где F1(–ae, 0), F2(ae, 0).

Доказательство. Повторив рассуждения доказательства предыдущей теоремы, получим:

(M, F1,2) = (a xe)2 . Откуда | (M, F1) – (M, F2)| = | a xe | | a xe | .

В случае гиперболы e > 1 и |x| a.

Если x a, то (a + xe) > 0 и (a – xe) < 0, поэтому | a xe | | a xe | = |a+xe– xe + a| = |2a| = 2a. Если x – a, то (a + xe) < 0 и (a–xe) > 0, поэтому | a xe | | a xe | = |–a–xe–a+xe| = |–2a| = 2a.

1. Эллипс

Определение 1. Эллипс — геометрическое место точек, сумма расстояний от которых, до двух фиксированных точек, называемых фокусами эллипса, есть величина постоянная (бόльшая, чем расстояние между фокусами) .

Обозначения: 2с— расстояние между фокусами,

2а — сумма расстояний от точек эллипса до фокусов ( c a ).

1. Каноническое уравнение эллипса:	x2	y2	1, где b	2	a	2	c	2	.
	a2	b2

2.Координаты фокусов: ( c;0), (c;0) .

3.Координаты вершин эллипса: ( a;0), (a;0); (0; b),(0;b) ; a — большая полуось эллипса,

Кафедра геометрии, СГУ, Мех-мат. Новиков В.Е.

b — малая полуось эллипса.

4.Эксцентриситет: e ac 1.

5.Уравнения директрис: x ae .

2.Гипербола

Определение 2. Гипербола – геометрическое место точек, абсолютная величина разности расстояний от которых, до двух фиксированных точек, называемых фокусами гиперболы, есть величина постоянная (меньшая, чем расстояние между фокусами) .

Обозначения: 2с- расстояние между фокусами,

2а - разность расстояний от точек гиперболы до фокусов ( c a ).

1. Каноническое уравнение гиперболы:	x2	y2	1, где b2	c2	a2 .
	a2	b2

2.Координаты фокусов: ( c;0), (c;0) .

3.Координаты вершин гиперболы: ( a;0), (a;0) .

a — действительная полуось гиперболы, b — мнимая полуось гиперболы.

4. Уравнения асимптот: y ba x .

5.	Эксцентриситет: e	c	1 .
5.	Эксцентриситет: e	a	1 .
		a	x a .
6.	Уравнения директрис:		x a .
			e
7.	Уравнение сопряженной гиперболы:			x2	y2	1.
7.	Уравнение сопряженной гиперболы:			a2	b2	1.
				a2	b2

8. Уравнение равносторонней гиперболы: x2 y2 a2 .

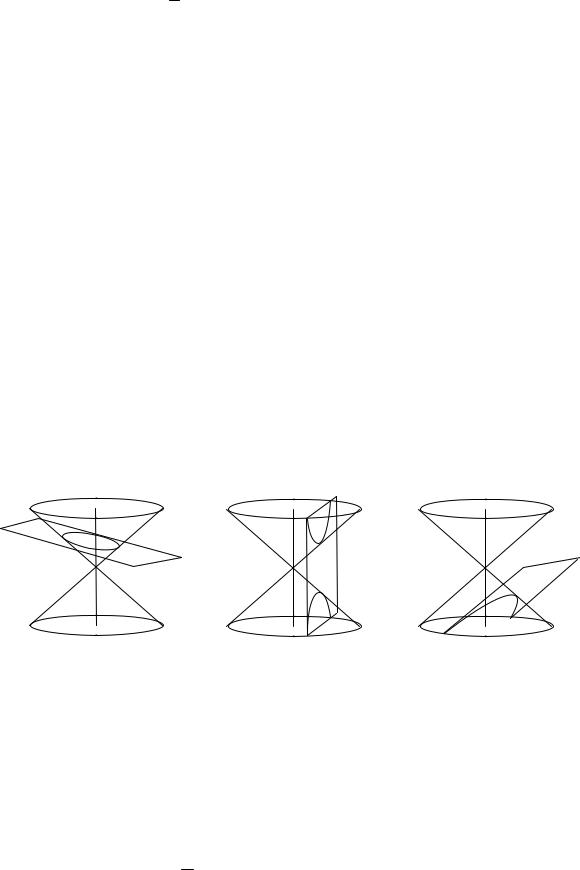
ЭЛЛИПС	ГИПЕРБОЛА	ПАРАБОЛА
Секущая плоскость пере-	Секущая плоскость	Секущая плоскость
секает все образующие	параллельна двум об-	параллельна одной
конуса	разующим конуса	образующей конуса

Рис. 4

3. Парабола

Определение 3. Парабола — геометрическое место точек, равноудаленных от данной точки, называемой фокусом гиперболы, и данной прямой, называемой директрисой. Обозначение: p — расстояние от фокуса до директрисы.

1.Каноническое уравнение параболы: y2 2 px .

2.Координаты фокуса: ( 2p ;0) .

3.Координаты вершины параболы: (0;0) .

<<< < Предыдущая 1 2 3 4 5 6 7 8 910 / 1210 11 12 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
16.04.2019108.54 Кб5Lektsia_16.doc
#
19.09.2019117.25 Кб4Lektsia_6.doc
#
19.09.2019275.97 Кб1Lektsia_7.doc
#
19.09.2019140.29 Кб1Lektsia_8.doc
#
09.06.2015584.79 Кб17lektsii_141_matan1.pdf
#
09.06.2015853.56 Кб110Lektsii_po_analiticheskoy_geometrii_Novikov.pdf
#
09.06.2015378.37 Кб7Lektsii_po_filosofii_2011.doc
#
29.03.2016871.98 Кб27Lektsii_TFKP.pdf
#
09.06.201521.62 Mб86leng_algebra.pdf
#
09.06.2015137.73 Кб63litologia.doc
#
09.06.2015599.6 Кб11Maciashek_978-5-94774-488-0_Glava1_cB488-0.pdf