Кафедра геометрии, СГУ, Мех-мат. Новиков В.Е.

4.Уравнение директрисы: x 2p .

5.Эксцентриситет: e 1.

ТЕОРЕМА 4.6 (Общее определение эллипса, гиперболы и параболы). Пусть на плоскости выбраны некоторая фиксированная точка F (фокус), некоторая прямая D (директриса), не содержащая эту точку F, и положительное число e. Тогда множество всех точек плоскости, отношение расстояний которых до точки F к расстоянию до прямой D равно e, есть эллипс, если

e < 1, или парабола, если e = 1, или гипербола, если e > 1.

Существуют и другие свойства, общие для эллипса, гиперболы и параболы. Используя метод сечений, все их можно получить как сечения кругового конуса (см. рис.4). Поэтому для эллипса, гиперболы и параболы принято общее название: конические сечения.

2.Фигуры второго порядка в пространстве; эллипсоиды, гиперболоиды, параболоиды, конусы и цилиндры второго порядка.

Приведение уравнений второй степени к каноническому виду

ТЕОРЕМА 4.7 (О каноническом уравнении фигуры второго порядка в пространстве). Существует такая декартова система координат, относительно которой всякую фигуру второго порядка в пространстве можно задать одним из следующих уравнений:

(группа 1)

37

Кафедра геометрии, СГУ, Мех-мат. Новиков В.Е.

(группа 4)

Доказательство этой теоремы проходит по той же схеме, что и доказательство теоремы 4.1 (О каноническом уравнении фигуры второго порядка на плоскости). Прежде всего, можно по-

казать, что алгебраическое уравнение фигуры второго порядка:

a11x2 + a22y2 + a33z2 + 2 a12xy + 2 a13xz + 2 a23yz + 2a1x + 2a2y + 2a3z + a = 0 (18)

Сначала при помощи лишь поворотов осей декартовой системы координат можно избавиться от одночленов с произведениями xy, yz, xz.

Затем с помощью выделения полного квадрата осуществить параллельный перенос осей декартовой системы к новому полюсу, который преобразует уравнение к одному из пяти урав-

нений (19) – (23).

ТЕОРЕМА 4.8 (Об ортогональных инвариантах). Ортогональными инвариантами (18) являются:

S = a11 + a22+ a33 — след матрицы малой квадратичной формы (18),

ским уравнением малой квадратичной формы (18), т.е. уравнение вида:

38

Кафедра геометрии, СГУ, Мех-мат. Новиков В.Е.

Корни этого уравнения 1, 2, 3, также ортогональные инварианты, являются действительными числами (показать самостоятельно).

Если > 0, то поверхность эллиптического типа; Если = 0, то поверхность параболического типа; Если < 0, то поверхность гиперболического типа;

Если 0, то поверхность не является ни цилиндром, ни конусом и не распадается на пару плоскостей.

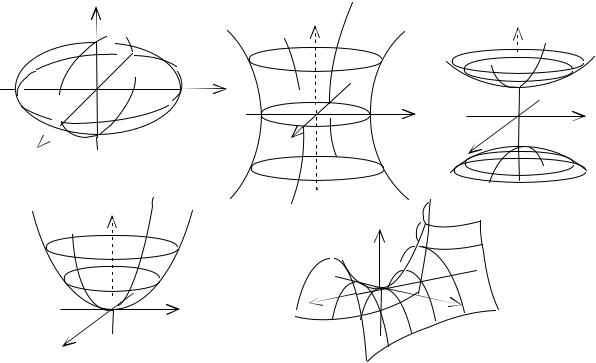
Эллипсоиды, гиперболоиды и параболоиды

Определение 4. Фигуры, которые могут быть заданы в некоторой декартовой системе координат уравнениями:

Рис. 8

Рис. 9

Линейчатые фигуры второго порядка в пространстве

Определение 5. Линейчатой фигурой называется фигура, которая является объединением прямых. Эти прямые называются прямолинейными образующими линейчатой фигуры.

К линейчатым фигурам очевидно относятся:

39

Кафедра геометрии, СГУ, Мех-мат. Новиков В.Е.

o Прямая;

o Пара плоскостей;

o Конусы (второго порядка);

o Цилиндры (эллиптические, гиперболические, параболические); Не очевидно линейчатыми фигурами являются:

o Однополостный гиперболоид; o Гиперболические параболоид.

Покажем это. Рассмотрим для этого следующие системы:

которые определяют пересечение двух плоскостей, т.е. два параметризованных семейства прямых. Перемножая эти уравнения, получим уравнение этих семейств:

3. Решение некоторых задач для фигур второго порядка.

Рассмотрим в общем случае, когда алгебраическая фигура задана уравнением f(x, y) = 0 (на плоскости) или f(x, y, z) = 0 (в пространстве), где функция f является непрерывно дифференцируемой по каждой переменной (такие функции также называют гладкими). В этом слу-

чае вектор N ( fx , f y ) (на плоскости) или N ( f x , f y , fz ) является нормальным вектором к соответствующей линии (на плоскости) или поверхности (в пространстве).

40