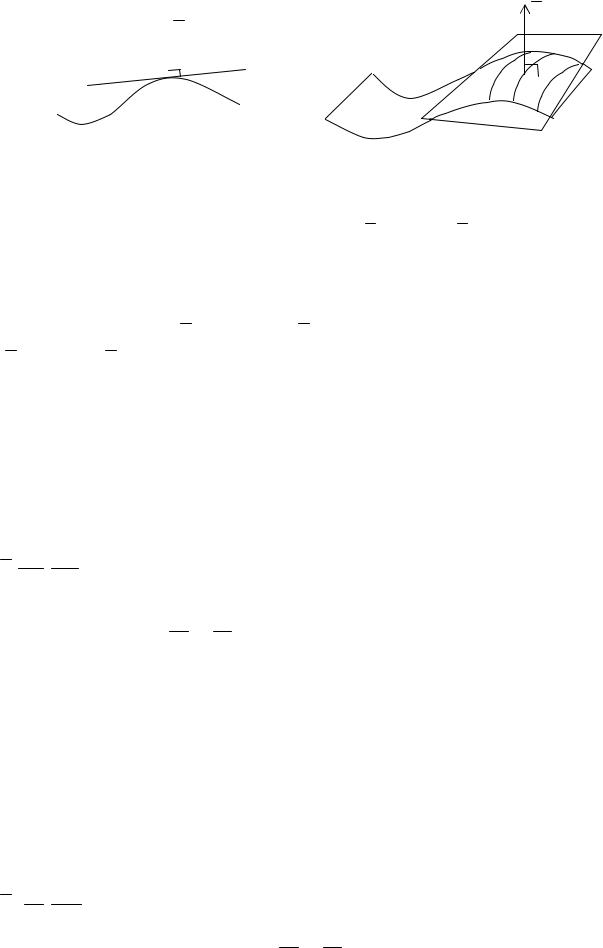
Кафедра геометрии, СГУ, Мех-мат. Новиков В.Е.

N ( f x , f y , fz )

N ( fx , f y )

Таким образом, эти векторы (см. рис. 12, рис. 13) являются нормальными векторами для соответствующей касательной прямой (на плоскости) или касательной плоскости (в пространстве).

Если кривые f(x, y) = 0 и g(x, y) = 0 пересекаются, то косинус угла пересечения равен модулю косинуса угла между нормальными векторами N1( f x , f y ) и N2 (gx , g y ) к этим кривым в

точке пересечения. Модуль берётся по той причине, что угол пересечения кривых по определению выбирается не тупой.

Если пересекаются поверхности f(x, y, z) = 0 и g(x, y, z) = 0, то аналогично косинус угла пересечения в точке M0, лежащей на кривой пересечения, равен модулю косинуса угла между

нормальными векторами N1( fx , f y , f z ) и N2 (gx , g y , gz ) . При этом векторное произведение

[ N1( fx , f y , f z ) , N2 (gx , g y , gz ) ] будет направляющим вектором касательной в точке M0 для

кривой, являющейся пересечением этих поверхностей. Рассмотрим частные случаи.

Линии на плоскости.

точка M0(x0, y0) F, т.е. её координаты удовлетворяют уравнению эллипса. В этой точке N ( 2ax20 , 2by20 ) вектор нормали к эллипсу, он же является нормалью касательной прямой к эл-

липса в точке M0. Следовательно, уравнение касательной в этой точке имеет вид: l: ax02 x by20 y C 0 (вектор нормали сократили на 2).

Осталось найти свободный коэффициент C. Ищем его из условия того, что точка M0(x0, y0) l,

N0 (ax02 , by20 ) нормальный вектор в точке M0(x0, y0). Уравнение касательной имеет вид: l: ax02 x by20 y 1.

41

Кафедра геометрии, СГУ, Мех-мат. Новиков В.Е.

Парабола F : y2 2 px,( p 0) . ПолучаемN ( 2 p,2y0 ) || N0 ( p, y0 ) нормальный вектор в

точке M0(x0, y0). Повторяя рассуждения, получаем уравнение касательной прямой в точке

M0(x0, y0):

l: px y0 y px0 0 или l: y0 y px px0 .

Поверхности в пространстве.

N ( ax02 , by20 , cz02 ) . Следовательно, касательная плоскость в этой точке имеет уравнение вида:

: ax02 x by20 y cz02 z D 0 .

Осталось найти свободный коэффициент D. Ищем его из условия M0(x0, y0, z0) :

N (ax02 , by20 , 1) — нормальный вектор в точке M0(x0, y0, z0) F;

: ax02 x by20 y z z0 0 или ax02 x by20 y z z0 — уравнение касательной плоскости в точке M0(x0, y0, z0).

Гиперболический параболоид F : x2 y2 2z : a2 b2

42

Параболический цилиндр F : y2 2 px,( p 0) :

N0 ( p, y0 ,0) — нормальный вектор в точке M0(x0, y0, z0) F;

: y0 y px px0 — уравнение касательной плоскости в точке M0(x0, y0, z0).

43