
- •Аннотация
- •Оглавление
- •Предисловие
- •ГЛАВА 1. Задачи оптимизации. Основные определения
- •1.1. Задачи оптимизации
- •1.2. Минимум функции одной переменной
- •1.3. Унимодальные функции
- •1.4. Выпуклые функции
- •1.5. Условие Липшица
- •1.6. Классическая минимизация функции одной переменной
- •Вопросы и задания для самоконтроля
- •ГЛАВА 2. Одномерная минимизация функций. Прямые методы
- •2.1. О прямых методах
- •2.2. Метод перебора
- •2.3. Метод поразрядного поиска
- •2.4. Метод дихотомии
- •2.5. Метод золотого сечения
- •2.6. Сравнение методов перебора, дихотомии и золотого сечения
- •2.7. Метод парабол
- •Вопросы и задания для самоконтроля
- •Задание для численной реализации в среде программирования MATLAB
- •ГЛАВА 3. Одномерная минимизация. Методы, использующие информацию о производных целевой функции
- •3.1. Метод средней точки
- •3.2. Метод хорд
- •3.3. Метод Ньютона
- •3.4. Возможные модификации метода Ньютона
- •3.5. Методы минимизации многомодальных функций
- •Вопросы и задания для самоконтроля
- •Задание для численной реализации в среде программирования MATLAB
- •ГЛАВА 4. Задача минимизации функции многих переменных. Необходимые и достаточные условия безусловного экстремума
- •4.1. Постановка задачи и определения
- •4.2. Свойства выпуклых множеств и выпуклых функций
- •4.3. Необходимые и достаточные условия безусловного экстремума
- •Вопросы и задания для самоконтроля
- •5.1. Выпуклые квадратичные функции
- •5.2. Общие принципы многомерной минимизации
- •5.3. Метод градиентного спуска
- •5.4. Метод наискорейшего спуска
- •5.5. Метод сопряженных направлений
- •5.6. Метод сопряженных градиентов
- •5.7. Метод Ньютона
- •5.8. Квазиньютоновские методы
- •Вопросы и задания для самопроверки
- •Задание для численной реализации в среде программирования MATLAB
- •ГЛАВА 6. Прямые методы безусловной минимизации многомерных задач
- •6.1. Проблема минимизации многомерных задач
- •6.2. Минимизация функций по правильному (регулярному) симплексу
- •6.3. Минимизация функций при помощи нерегулярного симплекса
- •6.4. Метод циклического покоординатного спуска
- •6.5. Метод Хука–Дживса
- •6.6. Методы случайного поиска
- •Вопросы и задания для самопроверки
- •Задание для численной реализации в среде программирования MATLAB
- •7.1. Условный экстремум при ограничениях типа равенств
- •7.2. Условный экстремум при ограничениях типа неравенств
- •Вопросы и задания для самопроверки
- •ГЛАВА 8. Линейное программирование
- •8.1. Определения. Примеры задач линейного программирования
- •8.2. Общая и каноническая задачи линейного программирования
- •8.3. Геометрическое истолкование задач линейного программирования
- •8.4. Аналитическое решение задач линейного программирования
- •Вопросы и задания для самоконтроля
- •Литература

В методе перебора точки xi , в которых определяются значения f (x) ,
выбираются заранее (прямые методы пассивного поиска). Если же для выбора очередной точки вычисления f (x) использовать информацию, содержащуюся в
уже найденных ее значениях, то поиск точки минимума можно сделать более эффективным, т.е. сократить число определяемых для этого значений f (x)
(прямые методы последовательного поиска). Метод поразрядного поиска является одним из таких методов.
Один из путей более эффективного поиска точки x |
следует из определения |
|||
унимодальных функций. Действительно, пусть |
a < x1 < x2 <b . Сравнив |
|||
значения f (x) в пробных точках x и |
x |
2 |
, можно сократить отрезок поиска точки x , |
|
1 |
|
|
|
|
перейдя к отрезку [a, x2 ] , если |
f (x1 ) ≤ f (x2 ) , или |
к отрезку [x1 , b], если |
||
f (x1 ) ≥ f (x2 ) . Описанную процедуру можно повторить необходимое число раз,
последовательно уменьшая отрезок, содержащий точку минимума.
Чтобы относительное уменьшение отрезка на каждой итерации не зависело от того, какая из его частей исключается из дальнейшего рассмотрения, пробные точки имеет смысл располагать симметрично относительно середины исходного отрезка. В зависимости от способа выбора пробных точек в этом случае получаются различные методы исключения отрезков. Рассмотрим только методы дихотомии и золотого сечения.
2.4.Метод дихотомии
Вэтом методе пробные точки x1 и x2 располагаются близко к середине очередного
отрезка [a, b] , т.е.
x = |
b + a −δ |
, |
x |
2 |
= |
b + a +δ |
, |
(2.3) |
|
|
|
||||||
1 |
2 |
|
|
2 |
|
|
||
|
|
|
|
|
|
|||
где δ − малое число. При этом отношение длин нового и исходного отрезков
τ = bb−−xa1 = xb2 −−aa близко к 12 , этим и объясняется название метода.
Отметим, что для любых точек x1 и x2 величина τ > 12 , поэтому указанный
выбор пробных точек объясняется стремлением обеспечить максимально возможное относительное уменьшение отрезка на каждой итерации поиска x .
24

Вконце вычислений методом дихотомии в качестве приближенного значения
xберут середину последнего из найденных отрезков [a, b] , убедившись
предварительно, что достигнуто неравенство b −2 a ≤ε .
Алгоритм метода деления отрезка пополам следующий.
Шаг 1. Определить x1 и x2 по формуле (2.3) и вычислить f (x1 ) и f (x2 ) .
Перейти к шагу 2.
Шаг 2. Сравнить f (x1 ) и f (x2 ) . Если f (x1 ) ≤ f (x2 ) , то перейти к отрезку [a, x2 ] , положив b = x2 , иначе − к отрезку [x1 , b], положив a = x1 . Перейти к шагу 3.
Шаг 3. Найти достигнутую точность |
εn = |
b − a |
(здесь n − номер итерации). |
|
|||
|
2 |
|
|
Если εn > ε , то перейти к следующей итерации, вернувшись к шагу 1. Если εn ≤ ε ,
то завершить поиск x , перейдя к шагу 4.
Шаг 4. Положить x ≈ x = a +2 b , f ≈ f (x) .
Необходимо обратить внимание на следующее.
1. Число δ из (2.3) выбирается на интервале (0, 2ε) с учетом следующих
соображений:
а) чем меньше δ , тем больше относительное уменьшение длины отрезка на каждой итерации;
б) при чрезмерно малом δ сравнение значений функции f (x) в точках x1 и x2 ,
отличающихся на величину δ , затруднительно, поэтому необходимо учитывать количество верных разрядов функции f (x) при задании аргумента x .
2.Число n итераций метода дихотомии, необходимое для определения точки
xс точностью ε , определяется неравенством
|
|
|
|
n ≥ log |
2 |
b − a −δ |
|
|
|
|
|
|
|
|
|
|
|
(2.4) |
||||||||
|
|
|
|
2ε −δ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
□ Обозначим длину [a, b]= 0 . Тогда длина отрезка, |
полученного после первой |
|||||||||||||||||||||||||
итерации, равна |
1 = |
0 |
+ δ |
, после второй итерации 2 |
= |
1 + |
δ |
= |
b − a |
+δ ( |
1 |
+ |
1 |
) , |
||||||||||||
2 |
2 |
|
4 |
|
||||||||||||||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
4 |
|
2 |
|
|||||
после третьей |
3 = |
2 |
+ δ |
= |
b − a |
+δ ( |
1 |
+ |
1 |
|
+ |
1 |
) и т.д. |
После |
n |
итераций |
длина |
|||||||||
2 |
|
|
4 |
|
2 |
|||||||||||||||||||||
|
|
2 |
8 |
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
25 |
||
отрезка |
поиска |
|
точки |
x |
|
станет |
|
|
|
|
равна |
|
n |
= |
b − a |
+δ ( |
1 |
|
+ |
|
1 |
|
+... + |
1 |
) |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
2n |
|
2n−1 |
2 |
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2n |
|
|
|
|
|
|
|
|
|
||||||
= |
b − a |
|
+ (1 − |
1 |
|
)δ . |
При |
этом |
будет |
достигнута |
точность |
определения точки |
||||||||||||||||||||||||||||||||||||||||||
2n |
2n |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
минимума |
εn |
= |
|
n |
. |
Находя |
n |
из |
условия εn = |
b − a |
+ (1 − |
|
1 |
) δ ≤ ε , |
получим |
|||||||||||||||||||||||||||||||||||||||
|
|
2n |
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2n+1 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|||||||||
неравенство (2.4). ■ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
3. |
|
Величина |
δ |
не |
|
может |
быть |
выбрана |
слишком |
большой. |
Так как |
|||||||||||||||||||||||||||||||||||||||||||
εn = |
b − a −δ |
|
+ |
|
δ |
≥ |
δ |
, но εn ≤ ε , необходимо выбирать δ < 2ε . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
2n+1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
4. |
|
При |
|
малом |
значении |
δ |
величина |
εn = |
b − a −δ |
|
+ δ |
≈ |
b − a |
. |
|
На |
|
каждой |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2n+1 |
|
|
|
|
2 |
|
|
|
2n+1 |
|
|
|
|
|
|
|
|||||
итерации метода дихотомии вычисляются два значения |
f (x) . |
|
Поэтому после |
N |
||||||||||||||||||||||||||||||||||||||||||||||||||
вычислений f (x) производится |
|
|
n = N / 2 |
итераций |
и |
достигается |
точность |
|||||||||||||||||||||||||||||||||||||||||||||||
определения x : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ε(N ) = ε N |
≈ |
b − a |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2.5) |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N |
+1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
Пример |
|
|
2.5. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
Методом |
деления |
|
|
|
|
отрезка |
|
пополам |
|
|
решить |
|
задачу |
|||||||||||||||||||||||||||||||||||||
f (x) = x4 |
+ e−x |
→ min, |
x [0, 1] , с точностью ε = 0,1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
□ Выберем δ = 0,02 , (δ < 2ε) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
Рассмотрим детально действия при итерации 1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
Шаг 1. |
|
x1 = 0,49, |
|
x2 |
= 0,51, |
f (x1 ) = 0,688, |
|
f (x2 ) = 0,670. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
Шаг 2. |
|
f (x1 ) > f (x2 ) , поэтому полагаем a = x1 = 0,49 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
Шаг 3. |
|
b − a |
|
= 0,255 > 0,1, поэтому переходим к следующей итерации. |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Исходные данные и результаты вычислений итераций приведены в табл. 2.2. |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
Результаты вычислений на итерациях 1 − 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 2.2. |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
Номер |
|
|
|
a |
|
|
|
|
b |
|
|
(b − a) / 2 |
|
|
|
|
x1 |
|
|
|
|
x2 |
|
f (x1 ) |
|
|
f (x2 ) |
|
|
Сравнение |
|
|
||||||||||||||||||||||
итерации |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
1 |
|
|
|
|
|
0 |
|
|
|
|
1 |
|
|
|
0,5 |
|
|
|
|
|
0,49 |
|
|
|
|
0,51 |
|
0,688 |
|
0,670 |
|
f (x1 ) > f (x2 ) |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
2 |
|
|
|
|
|
0,49 |
|
|
|
|
1 |
|
|
|
0,26 |
|
0,735 |
|
|
|
|
0,755 |
|
0,771 |
|
0,792 |
|
|
f (x1 ) < f (x2 ) |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
3 |
|
|
|
|
|
0,49 |
|
|
|
0,755 |
|
|
0,13 |
|
0,613 |
|
|
|
|
0,633 |
|
0,683 |
|
0,691 |
|
|
f (x1 ) < f (x2 ) |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
4 |
|
|
|
|
|
0,49 |
|
|
|
0,633 |
|
|
0,07 |
|
|
0,07 < 0,1 −точность достигнута |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
26 |
|

Откуда x ≈ |
0,49 + 0,633 |
≈ 0,56, f ≈ f (0,56) ≈ 0,67 (сравнить |
с расчетом примера |
|
|
||||
2 |
|
|
|
|
методами перебора и поразрядного поиска; вычислено 7 значений |
f (x) ). ■ |
|||
2.5. Метод золотого сечения |
|
|
||
Рассмотрим такое симметричное расположение точек x1 |
и x2 |
на отрезке [a, b] , |
||
при котором одна из них становится пробной точкой на новом отрезке, полученном после исключения части исходного отрезка. Использование таких точек позволяет на каждой итерации метода золотого сечения, кроме первой, ограничиться определением только одного значения f (x) , так как другое значение уже найдено на одной из предыдущих итераций.
Найдем точки x1 и x2 , обладающие указанным свойством.
Рассмотрим сначала отрезок [0,1] и для определенности предположим, что при его уменьшении исключается правая часть этого отрезка. Пусть x2 =τ , тогда симметрично расположенная точка x1 =1−τ (рис.2.1).
Рис.2.1. Иллюстрация выбора пробных точек в методе золотого сечения
Пробная точка x1 |
отрезка [0,1] перейдет в пробную точку |
x2′ =1 −τ |
нового |
|||||||
отрезка [0, τ] . Чтобы точки x2 =τ |
и x2′ =1 −τ |
|
делили отрезки [0,1] и [0, τ] в одном |
|||||||
и том же отношении, |
должно выполняться |
равенство |
1 |
= |
τ |
, или τ 2 |
=1 −τ , |
|||
|
1 −τ |
|||||||||
|
|
|
|
|
τ |
|
|
|||
откуда находим положительное значение τ = |
|
5 −1 ≈ 0,61803.... Таким образом, |
||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
x =1 −τ |
= 3 − 5 , |
x |
2 |
=τ = 5 −1 . |
|
|
|
||
|
1 |
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Для произвольного отрезка [a, b] выражения для пробных точек примут вид
27
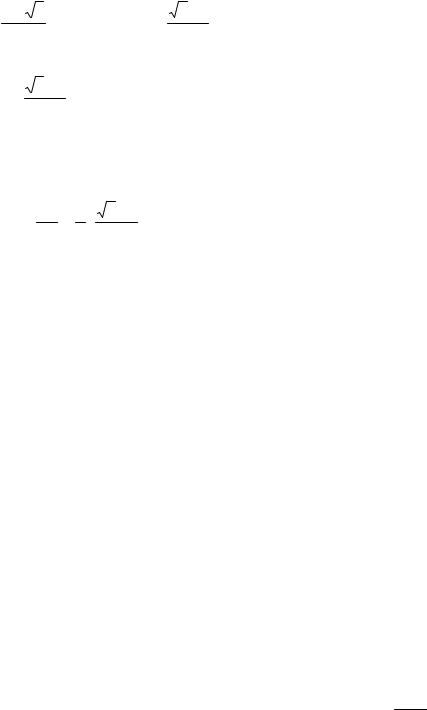
x = a + |
3 − 5 |
(b − a), x = a + |
5 −1 |
(b − a) . |
(2.6) |
1 |
2 |
2 |
2 |
|
|
|
|
|
|
На каждой итерации отрезок поиска точки минимума уменьшается в одном и
том же отношении τ = |
5 −1 |
, |
|
поэтому |
в результате n |
итераций его длина |
|||
|
2 |
|
|
|
|
|
|
|
|
становится n =τ n (b − a) . Таким образом, |
точность определения точки x после n |
||||||||
итераций находится из равенства |
|
|
|
|
|
|
|||
|
n |
|
|
1 |
|
5 −1 |
n |
|
|
εn = |
= |
|
|
|
|
(b − a) , |
(2.7) |
||
2 |
2 |
|
2 |
|
|||||
|
|
|
|
|
|
|
|||
а условием окончания поиска точки x с точностью ε служит неравенство εn ≤ ε .
Необходимо обратить внимание на следующее.
1. Точки x1 и x2 из (2.6) обладают следующим свойством: каждая из них делит отрезок [a, b] на две неравные части так, что отношение длины всего отрезка к длине его большей части равно отношению длин большей и меньшей части отрезка. Точки с таким свойством называются точками золотого сечения отрезка [a, b] . Это и объясняет название рассматриваемого метода.
2. На каждой итерации исключения отрезков с пробными точками (2.6) одна из
них переходит на следующий отрезок и значение |
f (x) в ней уже известно. |
3. Легко проверить, что x1 = a +b − x2 и x2 |
= a +b − x1 . Поэтому на каждой |
итерации метода золотого сечения недостающую пробную точку нового отрезка можно найти по перешедшей на него пробной точке с помощью сложения и вычитания, не используя (2.6).
4.В конце вычислений по методу золотого сечения в качестве приближенного значения x можно взять середину последнего из полученных отрезков x = a +2 b .
5.Число итераций, необходимое для достижения заданной точности ε , можно
найти из условия εn ≤ ε с учетом соотношения (2.7)
2ε |
|
b − a |
|
|||||
n ≥ ln |
|
|
|
|
/ lnτ = 2,1 ln |
|
. |
|
|
− a |
|
|
|||||
b |
|
|
2ε |
|
||||
Так как N вычислений f (x) |
позволяют выполнить N −1 |
итераций метода |
||||||
золотого сечения, то достигнутая в |
|
результате |
этого точность |
определения x |
||||
составляет |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
28 |
