дифференцируемыми на [a, b] функциями.

не убывает на

этом отрезке.

□ Пусть f (x) выпукла

на

[a, b] , тогда

f (x)

′

Допустим противное, т.е. что

f (x) не унимодальна на [a, b] .

Тогда существуют

x1 , x2 , x3 [a, b] такие, что

f (x1 ) < f (x2 ) и

f (x3 ) < f (x2 ) . А

это

противоречит

дифференциальному критерию "а" выпуклости f (x)

на [a, b] . ■

Определение. Функция f (x) удовлетворяет на отрезке [a, b]

условию

Липшица, если существует такое число L > 0 (константа Липшица), что

f (x′) − f (x′′)

≤ L

x′− x′′

(1.7)

для всех x′ и x′′, принадлежащих [a, b] .

Необходимо обратить внимание на следующее.

модуль ее углового коэффициента также не может превышать

L . Так, функция

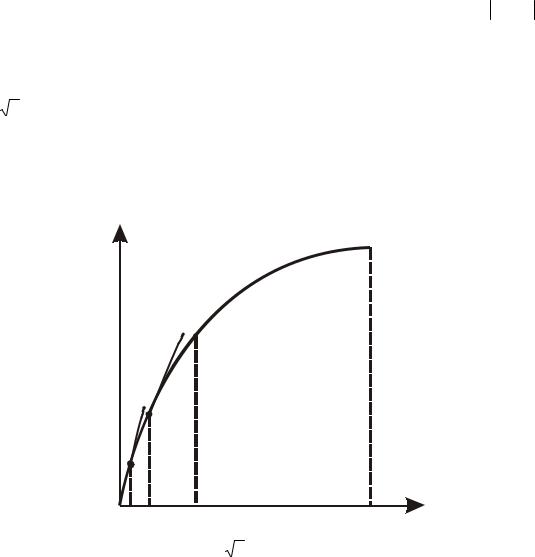
f (x) =

x на отрезке [0, 1] условию Липшица не удовлетворяет,

потому что при

x → +0

угловой коэффициент

касательной к ее графику k

неограниченно

возрастает (рис. 1.5).

y

f(x)

0,01 0,1

0,2

1

x

Рис.1.5. График функции

f (x) =

x , x [0, 1] , не удовлетворяющей условию

Липшица

она удовлетворяет на этом отрезке условию Липшица с константой L = max

f

′

.

(x)

Пример 1.9.

[a, b]

Найти наименьшую

из

констант

Липшица

функции

f (x) =

1

x3

+ 2x2

−5x + 6

на отрезках а)

x [0, 1]

, б)

x [0, 10] .

3

□ Производная функции f

′

2

+ 4x −5 = (x +5) (x −1) ,

поэтому в случае "а"

(x) = x

L = max

f

′

=

f

′

= 5 , а в случае "б"

L = max

′

=

′

=135

. ■

(x)

(0)

f (x)

f (10)

[0, 1]

[0, 10]

Пример 1.10. Показать, что для дифференцируемой на отрезке [a, b]

функции

f (x)

величина

L = max

f

′

представляет собой

минимальную из

констант

(x)

[a, b]

Липшица f (x) на [a, b] .

□ Пусть существует

L1

< L = max

f ′(x)

такая,

что

f (x′) − f (x′′)

≤ L1

x′− x′′

для

[a, b]

и переходя к пределу при

, получим

всех

′

′′

[a, b].

Тогда,

фиксируя x

′

x

′′

′

x , x

→ x

′

′

≤ L1

,

а

вследствие

произвольности

точки

′

[a, b]

получим

f (x )

x

max

′

≤ L1

< L

. Полученное противоречие доказывает утверждение. ■

f (x)

[a, b]

Пример 1.11. Найти наименьшую из

констант

Липшица

функции

f (x) =

4x3 −30x2

+ 72x +12 на отрезках а)

x [0, 2] , б) x [2, 3].

□

Производная

функции

f

′

=12x

2

−60x + 72 =12(x − 2) (x −3) ,

поэтому в

(x)

случае "а"

L = max

f

′

=

f

′

= 72 , а в случае "б"

L = max

f

′

=

f

′

= 3 . ■

(x)

(0)

(x)

(2,5)

[0, 2]

[2, 3]

Пример 1.12. Найти наименьшую из

констант

Липшица

функции

f (x) =

x3 + 6x2

−15x на отрезках а)

x [0, 1] , б)

x [0, 10] .

□ Производная функции f

′

2

+12x −15 = 3(x +5) (x −1) ,

поэтому в случае

(x) = 3x

"а"

L = max

f

′

=

f

′

=15 , а в случае "б"

L = max

′

=

f

′

= 405 . ■

(x)

(0)

f (x)

(10)

[0, 1]

[0, 10]

производные

f (x) до

(n −1) -го порядка включительно равны нулю, а

f

(n)

~

(x) ≠ 0 .

Тогда, если n

− нечетно, то точка x не является точкой локального экстремума

~

функции f (x) . Если же n − четное число, то:

а) при

f

(n)

~

~

− точка локального минимума

f (x) ;

(x) > 0

x

б) при

f

(n)

~

~

− точка локального максимума

f (x)

(x) < 0

x

′

(1.8)

f (x) = 0,

предложить

следующий

алгоритм

минимизации

f (x)

на

отрезке

[a, b]

(классический метод, который разберем на примере).

Пример 1.13. Решить задачу f (x) = x3 −3x +1 → min,

x [−2, 2].

□ Шаг 1. Находим корни уравнения

f

′

= 3x

2

−3 = 0

из интервала (−2, 2) :

(x)

x1 = −1, x2 =1.

Полагаем x0

= −2, x3

= 2.

Шаг

2.

Вычисляем

значения

f (x)

в

точках

xi ,

i = 0, ..., 3 :

f (x0 ) = −17,

f (x1 ) = 3,

f (x2 ) = −1,

f (x3 ) =1.

Шаг 3. Находим f

= min(−17, 3, −1, 1) = −17 = f (x0 ). Поэтому x = −2, f = −17. ■

Пример 1.14. Найти f (x) = x3 −27x +5 → min,

x [−4, 4].

□

Найдем

корни уравнения

′

= 3x

2

− 27 = 0 из

f (x)

интервала

x (−4, 4) :

x1

= −3, x2 = 3.

Положим

x0 = −4, x3

= 4.

Так

как

f ′′(x1 ) =

f ′′(−3) = −18 < 0 ,

то

x1

−

точка

локального максимума.

Так

как

f ′′(x2 ) =

f ′′(3) =18 > 0,

то

x2

точка

локального

минимума.

f (3) = −49,

f (−4) = 49,

f (4) = −39. Производя перебор, получим

x = 3, f = −49.