6.5. Метод Хука–Дживса

Эффективность прямого поиска точки минимума ограниченной снизу целевой функции можно повысить, если на каждом k -м шаге поиска последовательно выбирать направление спуска. Для этого на каждом k -м шаге выделяют предварительный этап исследующего поиска. Целью этого этапа является выбор

Алгоритм метода Хука–Дживса на каждом шаге содержит две основные процедуры:

а) исследующий поиск в окрестности данной точки x для определения направления убывания функции f (x) . В результате получим точку x ;

б) перемещение в направлении убывания (x − x) .

Поиск завершается, если после шага "а" получено, что x = x .

Опишем один из возможных алгоритмов исследующего поиска −

поиск окончен, т.е. получена точка x , для которой f (x) < f (x) , если В результате исследующего поиска может оказаться, что

исследующий поиск считается неудачным. Если при этом норма приращения

117

коэффициент дробления шага γ >1, параметр окончания поиска ε > 0 . Перейти к

и подобрать так называемый ускоряющий множитель ak > 0 , чтобы f (x1 ) < f (x 0 ) .

Часто ak (0,1]. С увеличением ak увеличивается длина ak x 0 − x0 шага спуска в направлении вектора x 0 − x0 . Значение ak можно подбирать из условия минимума функции f (x) при смещении точки x 0 в направлении этого вектора. В простейшем варианте метода Хука–Дживса значение ak выбирают постоянным, обычно ak = 2 .

В этом случае формула, по которой осуществляется спуск, имеет вид

x1 = x0 +2(x 0 − x0 ) = 2x 0 − x0 .

6.6. Методы случайного поиска

Основой для этих методов служит итерационный процесс

118

при помощи генерирования случайных векторов ξ получаются точки, лежащие на гиперсфере радиуса αk с центром в точке xk . Если значение функции в полученной точке не меньше, чем в центре сферы, шаг считается неудачным. Если число неудачных шагов из данной точки достигает заданного числа M , поиск повторяется из той же точки с уменьшенным шагом до тех пор, пока шаг не станет меньше заданной точности. Если же значение функции в полученной точке меньше, чем в центре, шаг считается удачным и полученное значение выбирается за новый центр поиска.

Приведем два возможных алгоритма метода случайного поиска. Они могут использоваться как самостоятельные минимизирующие процедуры, или входить в состав других алгоритмов, например, использоваться для исследующего поиска в методе Хука-Дживса.

Алгоритм поиска с возвратом при неудачном шаге следующий.

Шаг 1. Выбрать параметр точности ε > 0 , начальный шаг α > 0 , коэффициент уменьшения шага γ >1, предельное число попыток M , точку x . Вычислить f (x) .

Перейти к шагу 2.

Шаг 2. Положить счетчик числа неудачных попыток j =1. Перейти к шагу 3.

Шаг 3. Получить реализацию случайного вектора ξ . Перейти к шагу 4.

Шаг 4. Найти пробную точку y = x +α ξξ , вычислить f ( y) . Перейти к шагу 5.

Шаг 5. Если f ( y) < f (x) , то положить x = y, f (x) = f ( y) и перейти к шагу 4.

Иначе − перейти к шагу 6.

Шаг 6. Положить j = j +1. Если j ≤ M , то перейти к шагу 3, иначе − к шагу 7.

Шаг 7. Если α < ε , то поиск завершить, полагая x = x, f = f (x) . Иначе – положить α =α / γ и прейти к шагу 2.

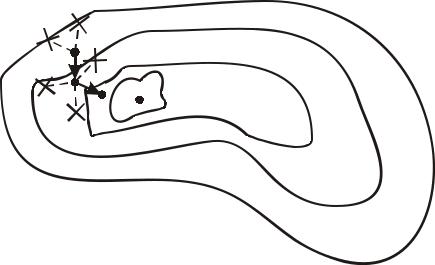
Иллюстрация построения последовательности (6.8) с помощью описанного алгоритма для функции двух переменных приведена на рис. 6.10, где пунктиром показаны неудачные попытки определения точки xk +1 из (6.8), не приводящие к уменьшению f (x) .

На практике предельное число неудачных попыток M обычно полагают равным 3n , где n − число переменных целевой функции.

119