Результаты вычислений примера методом хорд

Таблица 3.2.

′ ~

Номер

a

b

~

~

x

f (x )

Знак f (x )

итерации

′

-0,766

1

0

1

0,216

-

-0,528

2

0,216

1

0,352

-

-0,319

3

0,352

1

0,435

-

-0,175

4

0,435

1

0,480

-

-0,091

5

0,480

1

0,504

-

-0,046

6

0,504

1

0,516

точность

достигнута

Отсюда x ≈0,516 ,

f ≈ 0,668 . ■

До сих пор предполагалось, что

′

′

′

на концах

f (a) f

(b) <0 , т.е. производная

f (x)

Так,

если f

′

′

> 0 ,

то f (x) возрастает на [a, b], следовательно, x

= a , а

(a) , f

(b)

′

′

< 0

она убывает и x

= b .

при f (a) , f (b)

В случае f

′

′

= a

или x

= b , в зависимости от того,

на каком из

(a)

f (b) = 0 x

концов отрезка [a, b]

производная

f

(x) =0 .

′

3.3. Метод Ньютона

Если

выпуклая

на

отрезке

[a, b] функция

f (x) дважды непрерывно

дифференцируема на этом отрезке,

то точку x [a, b] минимума этой функции

можно найти, решая уравнение f

(x) =0

методом Ньютона (другое название −

′

метод касательных).

Пусть

x0 [a, b] −

нулевое

(начальное) приближение к

искомой точке

.

′

x

Линеаризуем функцию F(x) = f (x) в окрестности начальной

точки, приближенно заменив дугу

графика этой функции касательной в точке

(x0 , f ′(x0 ))

F(x) ≈ F(x0 ) + F ′(x0 )(x − x0 ) .

(3.3)

Выберем в

качестве

следующего приближения

к x точку x

пересечения

1

первый элемент

x

= x

0

−

F(x0 )

итерационной последовательности {x

k

}, k =1, 2, ....

1

F ′(x0 )

первый элемент x

= x

0

−

F(x0 )

итерационной последовательности {x

k

}, k =1, 2, ....

1

F ′(x0 )

В очередной точке xk

построим линейную аппроксимирующую функцию для

F (x) и определим точку,

в которой эта функция обращается в нуль, используя в

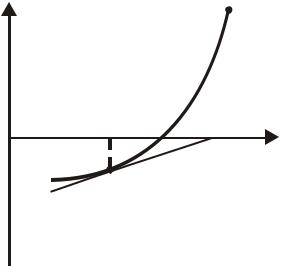
качестве следующего приближения xk +1 (рис. 3.3).

y

F(x)=f΄(x)

x*

x

xk

xk+1

Рис. 3.3. Иллюстрация метода касательных

Уравнение

касательной

к

графику

F(x)

в

точке

x = xk

имеет

вид

y = F(xk ) + F ′(xk ) (x − xk ) , поэтому

точка

x = xk +1 ,

найденная

из условия

y = 0 ,

F(xk )

′

определяется формулой xk +1

= xk −

. Поскольку

F(x) ≡ f (x) , получим, что для

F ′(xk )

′

необходимо построить последовательность

решения уравнения f (x) =0

xk +1 = xk

−

f ′(xk )

,

k =1, 2, ...

(3.4)

f ′′(xk )

где x0 − точка,

выбранная в качестве начального приближения. Вычисления по

формуле (3.4)

производятся

до

тех

пор, пока

не выполнится

неравенство

f ′(xk )

≤ ε , после чего полагают x ≈ xk ,

f ≈ f (xk ) .

xk

xk+1 x*

x

Рис. 3.4. Иллюстрация вывода формулы (3.4)

Для квадратичной функции

f (x) функция

′

линейна, поэтому в (3.4)

f (x)

случае, если f (x)

− трижды непрерывно дифференцируемая выпуклая функция.

′

) , где

x

− искомый корень, в окрестности k -

Напишем формулу Тейлора для f (x

го приближения

′′′

2

′

) = 0 =

′

′′

− xk ) +

f (ξ)

(x

− xk )

,

f (x

f (xk ) +

f (xk ) (x

2

а точка ξ [x , xk ] .

Разделив последнее соотношение на

f ′′(xk ) и перенеся первые два слагаемых

из правой части в левую, получим

′

1

′′′

xk

−

f (xk )

− x

=

f (ξ)

(xk

− x )2 ,

f ′′(xk )

2 f ′′(xk )

что, учитывая (3.4), переписываем в виде

xk +1 − x =

1

f ′′′(ξ)

(xk − x )2 ,

2

f ′′(xk )

1

M 3

x0

− x

<1.

(3.7)

2

m2

x − xk +1

x

− xk +

f ′(xk )

=

f ′′(xk )

=1 −

2

.

x

− xk

x

− xk

′′′

− xk )

2

2

+

f (x)(x

f ′(xk )

Отсюда следует, что последовательность {xk } монотонная, если

f ′′′(x)

> 0 , т.е.

f ′(xk )

достаточным условием

монотонной сходимости

метода

Ньютона является

постоянство в диапазоне

x [x

′′′

и совпадение его со

, x0 ] знака производной f (x)

о второй производных

f (x) в точке xk ,

с высокой точностью аппроксимирует

выпуклую

дважды дифференцируемую

функцию

f (x) в достаточно

малой

окрестности этой точки.

Поэтому,

если очередное приближение xk

оказывается

достаточно близким к x , то точки минимума xk +1

и x функций

qk (x)

и f (x)

практически совпадают.

Пример

3.3.

Методом Ньютона найти

точку

минимума

функции

f (x) =

1

2

) с точностью

′

−7

.

x arctg x −

ln(1 + x

f

(x)

≤10

2

′

1

□ Производные

функции

равны

= arctg(x),

′′

f (x)

f (x) = 1 + x2 > 0 ,

′′′

2x

. Видно, что при всех значениях переменной

′

′′′

<0 , т.е.

f (x) = − (1 + x2 )2

f (x)

f (x)

начальное приближение x0 =1

и построим приближения xk

по формуле (3.4),

результаты записаны в табл. 3.3.

Результаты минимизации функции методом Ньютона

Таблица 3.3.

k

xk

f ′(xk )

0

1

0,785

1

-0,570

-0,519

2

0,117

0,116

3

-1,061 10-3

-1,061 10-3

4

9 10-8

9 10-8