Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный исследовательский университет «МИЭТ»

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Книга_МО.pdf

Скачиваний:

554

Добавлен:

05.06.2015

Размер:

12.36 Mб

Скачать

☆

<<< < Предыдущая 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 2526 / 3326 27 28 29 30 31 32 33 > Следующая >>>

8.Назвать класс целевых функций, при минимизации которых метод НелдераМида имеет преимущество перед минимизацией по регулярному симплексу.

9.Сформулировать теоретическое обоснование минимизации целевой функции методом Нелдера-Мида.

10.Назвать класс унимодальных целевых функций, для которых эффективна минимизация методом циклического покоординатного спуска.

11.Как можно дополнительно повысить эффективность поиска точки минимума целевой функции, которая ищется методом циклического покоординатного спуска?

12.В чем состоит стратегия метода Хука-Дживса?

13.Какие подходы для реализации исследующего поиска в методе ХукаДживса Вы знаете? В чем состоит метод исследующего покоординатного поиска?

14.Перечислите способы выбора ускоряющего множителя в методе ХукаДживса при перемещении в направлении убывания.

15.Какие алгоритмы случайного поиска Вы знаете?

16.От какого параметра в наибольшей степени зависит эффективность алгоритмов случайного поиска?

17.На основе собственного опыта дать сравнительный анализ прямых методов.

Задание для численной реализации в среде программирования MATLAB

1.Реализовать в среде MATLAB методы правильного симплекса, НелдераМида, циклического покоординатного спуска, метод Хука-Дживса и метод случайного поиска.

2.Протестировать работу реализованных методов на примере "овражной" функции

f (x) = x12 +a x22 ,

при a = 1, 100, 500, 1000. Графически отобразить линии уровня функции. Сравнить скорость работы методов при различных значениях параметра a по числу итераций и по числу вызовов функций. Параметр точности выбрать ε =10−3 и ε =10−5 .

3. Выбрать для выполнения работы тестовую функцию, номер которой соответствует номеру Вашего компьютера. Например, для компьютера №3 это

121

будет функция 3), для компьютера №13 – функция 4): 13-9=4; для компьютера №23 это будет функция 5): 23-9×2=5.

1)f (x) = 64x12 +126x1 x2 +64x22 −10x1 +30x2 +13

2)f (x) =129x12 −256x1 x2 +129x22 −51x1 −149x2 −27

3)f (x) = 254x12 +506x1 x2 + 254x22 +50x1 +130x2 −111

4)f (x) =151x12 −300x1 x2 +151x22 +33x1 +99x2 +48

5)f (x) =85x12 +168x1 x2 +85x22 +29x1 −51x2 +83

6)f (x) = 211x12 −420x1 x2 +211x22 −192x1 +50x2 −25

7)f (x) =194x12 +376x1 x2 +194x22 +31x1 −229x2 +4

8)f (x) = 45x12 −88x1 x2 +45x22 +102x1 +268x2 −21

9)f (x) = 99x12 +196x1 x2 +99x22 −95x1 −9x2 +91

4.Графически отобразить линии уровня выбранной функции. Сравнить

эффективность метода покоординатного циклического спуска и метода ХукаДживса для задачи п.2 при а=250 и тестовой функции п.3 по числу итераций. Для метода Хука-Дживса величину шага исчерпывающего спуска выбирать по приближенной формуле и вычислять методом поразрядного поиска. Объяснить полученные результаты.

5. Используя методы прямого поиска, минимизировать функцию Розенброка

f(x) =100(x12 − x2 )2 +(x1 −1)2

сточностью ε =10−3 и ε =10−5 , контролируя точность алгоритмов исчерпывающего

спуска. Начальное приближение x0 = (−1, 1)T . Установить, какие из примененных алгоритмов не позволяют при заданной точности поиска получить точку минимума x* = (1, 1)T вследствие преждевременного окончания процесса поиска.

6.На примере функции Розенброка провести сравнение прямых и градиентных методов минимизации. Определить, сколько итераций потребуется каждому методу для того, чтобы разность между численным и точным решением была меньше ε .

7.На примере функции Химмельблау

f (x) = (x12 + x2 −11)2 +(x1 + x22 −7)2

122

(0, 0)

рассмотреть особенности применения прямых методов для минимизации многомодальных функций. В качестве начального приближения взять точки и (−5, 0) . Как зависит работа рассматриваемых алгоритмов от выбора начального приближения?

8. Встроенная функция Matlab fminsearch реализует метод Нелдера-Мида. Сравнить результаты ее работы с результатами, полученными Вашим алгоритмом. В каких случаях построенный Вами алгоритм работает эффективнее функции fminsearch?

123

ГЛАВА 7

Условный экстремум функции многих переменных. Необходимые и достаточные условия условного экстремума

Пусть даны	дважды		непрерывно		дифференцируемая	целевая	функция
f (x) = f (x1 , ..., xn )	и	функции		ограничений g j (x) = g j (x1 , ..., xn ) = 0,			j =1, ..., m ,
определяющие множество допустимых решений U .
Требуется исследовать			функцию f (x)		на экстремум, т.е.	определить точки
x U ее локальных минимумов и максимумов
	f (x ) = min f (x) ,			f (x ) = max f (x) ,			(7.1)
где U = {x : g j (x) = 0,		x U			x U
		j =1, ..., m;		m < n}. В первой части главы будем рассматривать

условные экстремумы с ограничениями только типа равенств.

7.1. Условный экстремум при ограничениях типа равенств

Определение. Функция

L(x, λ0 , λ) = λ0 f (x) + ∑λj g j (x) (7.2)

j=1

называется обобщенной функцией Лагранжа, числа λ0 , λ1 , ..., λm − множителями Лагранжа. Классической функцией Лагранжа называется функция

m
L(x, λ) = f (x) + ∑λj g j (x)	(7.3)
j=1

Определение. Градиентами обобщенной и классической функций Лагранжа по x называются вектор-столбцы, составленный из соответствующих частных производных первого порядка по xi , i =1, ..., n :

	∂L(x, λ0	, λ)
	∂x1
	∂x1
	...		,
x L(x, λ0 , λ) =	...		,
	...
	∂L(x, λ0	, λ)
	∂L(x, λ0	, λ)
	∂xn
	∂xn
	∂L(x, λ)
	∂x1
	∂x1
	...
x L(x, λ) =	...	.
	...
	∂L(x, λ)
	∂xn
	∂xn

(7.4а)

(7.4б)

124

Определение. Вторым дифференциалом обобщенной (классической) функции Лагранжа L(x, λ0 , λ) ( L(x, λ) ) называется функция

∂

L(x, λ0

, λ)

d 2 L(x, λ0 , λ) = ∑∑

dxi d x j ,

(7.5а)

∂xi ∂x j

i=1 j=1

∂

L(x, λ)

d 2 L(x, λ) = ∑∑

dxi d x j .

(7.5б)

i=1 j=1

∂xi ∂x j

Определение. Первым дифференциалом ограничения

g j (x)

называется

функция

∂g j (x)

d g j (x) = ∑

dxi , j =1, ..., m .

(7.6)

i=1

∂xi

Пример 7.1. Выписать функции (7.2)−(7.6) для задачи поиска условного

экстремума функции

f (x) = x12 + x22

на множестве U = {x : x22 − x1 + 3 = 0}, заданном

ограничением

(x) = x2 − x + 3 = 0 .

□ Обобщенная функция Лагранжа L(x, λ

, λ ) = λ

(x2

+ x2 ) + λ (x2

− x

+ 3) .

Классическая функция Лагранжа

L(x, λ ) = x2 + x

+ λ (x2

− x

+3) .

Градиент функций Лагранжа

L(x, λ

, λ ) = (2λ

x − λ ; 2λ

+ 2λ x

)T ;

L(x, λ ) = (2x − λ ; 2x

+ 2λ x

)T .

0 1

Второй дифференциал функций Лагранжа

2 L(x, λ

, λ ) = 2λ

d x2

+ ( 2λ

+ 2λ )dx 2

;

d 2 L(x, λ ) = 2d x2

+ ( 2 + 2λ )dx2 .

Первый дифференциал ограничения d g1 (x) = −dx1 + 2x2 dx2 . ■

Стратегия поиска локальных экстремумов

Находятся

точки

локальных

экстремумов

помощью

необходимых и

достаточных условий минимума и максимума первого и второго порядка при ограничениях типа равенств (порядок условий определяется порядком используемых производных). Вычисляются значения f (x ) в найденных точках локального экстремума.

Необходимые условия экстремума первого порядка. Пусть x − точка локального экстремума в задаче (7.1). Тогда найдутся числа λ0 , λ1 , ..., λm , не равные одновременно нулю и такие, что выполняются следующие условия:

− стационарности обобщенной функции Лагранжа по x

125

∂L(x , λ0	, λ )	= 0, i =1, ..., n ;
∂xi		= 0, i =1, ..., n ;
∂xi

− допустимости решения

g j (x ) = 0, j =1, ..., m .

(7.7а)

(7.7б)

	Если при этом градиенты g1 (x ), ..., gm (x )							в точке	x линейно независимы
(выполняется условие регулярности), то λ0 ≠ 0 .
	Важно отметить следующие моменты.
	1. Условие (7.7а) может быть записано в векторной форме x L(x , λ0 , λ ) = 0 .
	2.	Система		(7.7) содержит	(n + m)	уравнений с			(n + m +1) неизвестными
λ	, λ	, ..., λ ,	x	, ..., x . Точки x ,	удовлетворяющие системе при некоторых λ , λ ,
0	1	m	1	n					0
называются условно-стационарными.
	3. При решении задач проверка регулярности затруднена, так как точка									x
заранее неизвестна. Поэтому, как правило,							рассматриваются два случая: λ0 = 0			и
λ0	≠ 0 . Если λ0			≠ 0 , в системе (7.7а) полагают λ0				=1 . Это эквивалентно делению
						λj
системы уравнений (7.7а) на λ0 и замене							на λj	. При этом обобщенная функция
системы уравнений (7.7а) на λ0 и замене							на λj	. При этом обобщенная функция
						λ0

Лагранжа становится классической, а сама система (7.7) принимает вид

∂L(x , λ ) = 0,	i =1, ..., n,	(7.8а)
∂xi		(7.8а)
g j (x ) = 0,	j =1, ..., m	(7.8б)
где число уравнений равно числу неизвестных.
Определение. Точка экстремума,	удовлетворяющая системе (7.7) при	λ0 ≠ 0 ,
называется регулярной, а при λ0 = 0 − нерегулярной.

Случай λ0 = 0 отражает вырожденность ограничений. При этом в обобщенной функции Лагранжа исчезает член, содержащий целевую функцию, а в необходимых условиях экстремума не используется информация, представляемая градиентом целевой функции.

126

Необходимые условия экстремума второго порядка. Пусть x − регулярная точка минимума (максимума) в задаче (7.1) и имеется решение (x , λ ) системы

(7.8). Тогда второй дифференциал классической функции Лагранжа, вычисленный в точке (x , λ ) , неотрицателен (неположителен):

d 2 L(x , λ ) ≥ 0				( d 2 L(x , λ ) ≤ 0 )	(7.9)
для всех d x таких, что
n
n	∂ g j	(x )
d g j (x ) = ∑	∂ g j	(x )		d xi = 0, j =1, ..., m .	(7.10)
d g j (x ) = ∑				d xi = 0, j =1, ..., m .	(7.10)
=	∂x		i
i 1			i

Достаточные условия экстремума. Пусть имеется точка (x , λ ) ,

удовлетворяющая системе (7.8). Если в этой точке d 2 L(x , λ ) > 0 , (соответственно,

d 2 L(x , λ ) < 0 ) для всех ненулевых d x таких, что

n
n	∂ g j (x )
d g j (x ) = ∑	∂ g j (x )		d xi = 0,	j =1, ..., m ,
d g j (x ) = ∑			d xi = 0,	j =1, ..., m ,
=	∂x	i
i 1		i
то точка x является точкой	локального			минимума (максимума) задачи

экстремума.

Достаточные и необходимые условия экстремума второго порядка проверяются в условно-стационарных точках, которые удовлетворяют системе (7.7) при λ0 ≠ 0

или системе (7.8), так как для практики представляет интерес случай, когда в функции Лагранжа присутствует целевая функция, экстремум которой ищется.

Алгоритм решения задачи следующий.

Шаг 1. Составить обобщенную функцию Лагранжа

L(x, λ0 , λ) = λ0 f (x) + ∑λj g j (x) .

j=1

Шаг 2. Записать необходимые условия экстремума первого порядка

а)	∂L(x , λ0	, λ )	= 0, i =1, ..., n ;
	∂xi

Шаг 3. Решить систему для двух случаев

1)λ0 = 0 ;

2)λ0 ≠ 0 (при этом поделить условие а) на

б) g j (x ) = 0, j =1, ..., m .

		λj
λ0	и заменить		на λj ).
λ0	и заменить		на λj ).
		λ0

127

В результате найти условно-стационарные точки x , выделив из них

полученные при λ0 ≠ 0 (они могут быть регулярными точками экстремума).

Шаг 4. Для выделенных на шаге 3 точек проверить достаточные условия экстремума:

а) записать выражение для второго дифференциала классической функции Лагранжа в точке (x , λ )

n n	2	L(x		) dxi d x j ;
d 2 L(x , λ ) = ∑∑∂		L(x	, λ	) dxi d x j ;
i=1 j=1		∂xi ∂x j

б) записать систему дополнительных условий в точке x

d g j (x ) = ∑∂ g j (x			) d xi = 0, j =1, ..., m ;
n
=	∂x	i
i 1		i

в) из последних условий выразить любые из m дифференциалов d xi через остальные (n − m) и подставить в d 2 L(x , λ ) ;

г) если d 2 L(x , λ ) > 0 при ненулевых d x , то в точке x − условный локальный минимум. Если d 2 L(x , λ ) < 0 при ненулевых d x , то в точке x − условный локальный максимум. Если достаточные условия экстремума не выполняются, следует проверить выполнение необходимых условий второго порядка, следуя аналогичной процедуре. Если они выполняются, то требуется дополнительное исследование, в противном случае в точке x нет условного экстремума.

Шаг 5. Вычислить значения функции в точках условного экстремума.

Приведем в виде таблицы результаты исследования на наличие в точке x локальных экстремумов при соблюдении необходимых условий первого порядка

∂L(x , λ0	, λ )	= 0, i =1, ..., n ,
∂xi		= 0, i =1, ..., n ,
∂xi

g j (x ) = 0, j =1, ..., m ,

причем λ0 ≠ 0 (табл. 7.1).

128

	Результаты исследования локальных экстремумов в точке x				при соблюдении
		необходимых условий первого порядка			Таблица 7.1.

№	d 2 L(x , λ )	d g j (x ) j =1,..., m		Тип условно-стационарной точки x

1	> 0	0,	dx ≠ 0	Условный локальный минимум

2	<0	0,	dx ≠ 0	Условный локальный максимум

3	≥0		0	Может быть условный локальный минимум,
	≥0		0	требуется дополнительное исследование
				требуется дополнительное исследование

4	≤ 0		0	Может быть условный локальный максимум,
	≤ 0		0	требуется дополнительное исследование
				требуется дополнительное исследование

5	= 0		0	Требуется дополнительное исследование

6	> 0, < 0		0	Нет экстремума

Пример 7.2. Найти f (x) = x 2		+ x 2	→ extr		при условии g				1	(x) = x + x	2	− 2 = 0 .
	1	2							1	1	2
□ Проверим условие регулярности.					Так	как		g1 (x) = (1, 1)T			≠ 0 , то условие
выполняется. Поэтому будем пользоваться классической функцией Лагранжа.
1.	Составим функцию Лагранжа
	L(x, λ ) = x2			+ x2	+ λ (x + x		2	− 2) .
		1	1	2	1	1	2
2.	Выпишем необходимые условия экстремума первого порядка

а)	∂L(x, λ1 ) = 2x + λ = 0,
	1	1
	∂x1

б) g1 (x) = x1 + x2 − 2 = 0 .

3.Решение системы: x1 =

4.Проверим достаточные

∂L(x, λ1 ) = 2x	2	+ λ = 0,	откуда	x = − λ1		, x	2	= − λ1	;
∂x2	2	1		1	2		2	2
∂x2					2			2

x2 =1, λ1 = −2 − условно-стационарная точка.

условия экстремума

а)

d 2 L(x , λ ) = 2dx2

+ 2dx2 ,

так как

∂

2 L(x,

λ )

∂2 L(x, λ )

= 2 ,

∂2 L(x,

λ )

= 0 ,

∂x2

∂x ∂x

∂x2

∂2 L(x, λ )

= 0;

∂x

б)

d g

(x ) = dx

+ dx

= 0 , так как

∂g1 (x)

=1;

∂x1

∂x2

в) выразим дифференциал dx через

dx = −dx

и подставим в

d 2 L

г) так как d 2 L(x , λ ) = 4dx2

> 0 при

≠ 0 , то в точке x = (1, 1)T

− регулярный

локальный условный минимум.

129

5. Вычислим значение функции в точке условного экстремума: f (x ) = 2 . ■

Графическое решение задачи приведено на рис.7.1.

f(x) = x12 + x22

x1 + x2 - 2 = 0

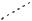2 x2 x* = (1 , 1)T

Рис.7.1. Иллюстрация к решению задачи из примера 7.2 Пример 7.3. Найти условный экстремум

f (x) = x1 + x2 →extr ,

g1 (x) = x12 + x22 − 2 = 0 .

□ Проверим условие регулярности. Так как g1 (x) = (2x1 , 2x2 )T ≠ 0 для всех x U , то условие регулярности выполняется. Поэтому будем пользоваться

классической функцией Лагранжа.
1.	Составим функцию Лагранжа
										L(x, λ ) = x + x								2	+ λ (x2 + x2 − 2) .
											1				1			2	1	1			2
2.	Выпишем необходимые условия экстремума первого порядка
а)		∂L(x, λ1 )				=1 + 2λ x				= 0,			∂L(x, λ1 )				=1 + 2λ x					2	= 0,	откуда x = −			1	,	x	2	= −	1	;
а)						=1 + 2λ x				= 0,							=1 + 2λ x						= 0,	откуда x = −				,	x		= −		;
			∂x1				1	1						∂x2						1					1		2λ1					2λ1
			∂x1											∂x2													2λ1					2λ1
б) g			(x) = x2 + x2 − 2 = 0 .
	1				1		2
3.	Решением системы являются две условно-стационарные точки
		A :		x	= x		=1,		λ		= −	1				B :			x = x				= −1,	λ =	1	.
		A :		x	= x		=1,		λ		= −					B :			x = x		2		= −1,	λ =		.
				1	2					1	2								1		2			1	2
											2														2
4.	Проверим достаточные условия экстремума

130

а) d 2 L(x , λ ) = 2λ dx2 + 2λ dx2 , так как

∂2 L(x, λ )

= 2λ ,

∂x2

1 2

∂x2

∂2 L(x,

λ )

∂2 L(x,

λ )

= 0 ;

∂x ∂x

∂x

б) d g

(x ) = 2x dx

+ 2x dx

= 0 , так как

∂g1 (x) = 2x ,

∂g1 (x) = 2x

;

∂x1

∂x2

в) Исследуем точку A . Получаем d g1 ( A) = 2dx1 + 2dx2 = 0 , откуда dx1

= −dx2 .

С учетом полученного соотношения d

2 L( A) = −dx2

− dx2

= −2dx2

< 0

при

≠ 0 .

Поэтому в точке x

= (1, 1)T имеем регулярный условный локальный максимум.

Исследуем точку B . Получаем d g1 (B) = −2dx1 − 2dx2

= 0 , откуда dx1 = −dx2 .

С учетом полученного соотношения d

2 L(B) =dx

+ dx2 = 2dx2

> 0

при dx

≠ 0 .

Поэтому в точке x

= (−1, −1)T

имеем регулярный условный локальный минимум.

5. Подсчитаем значения функции в точках экстремума

f ( A) = 2,

f (B) = −2 . ■

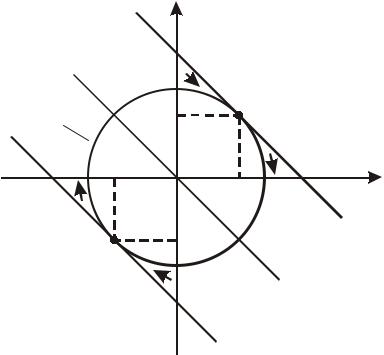
Графическое решение задачи представлено на рис. 7.2.

g2(x) = x12+x22 - 2 = 0

-1

-2

-1

f(x) = 2

-2

f(x) = 0

f(x) = -2

Рис.7.2. Иллюстрация к решению задачи из примера 7.3 Пример 7.4. Найти условный экстремум в задаче

f (x) = x1 →extr ,

g1 (x) = x22 − x13 = 0 .

131

□ Проверим условие регулярности.										Так как				g	(x) = (−3x2	, 2x		2	)T = 0 в точке
														1	1			2
x = (0, 0)T , то			условие			регулярности					не выполняется. Будем пользоваться
алгоритмом с использованием обобщенной функции Лагранжа.
1.	Составим обобщенную функцию Лагранжа
							L(x, λ	0	, λ ) = λ	0	x + λ (x		2	− x3 ) .
								0	1	0	1	1	2	1
2.	Выпишем необходимые условия экстремума первого порядка
а)	∂ L(x, λ0 , λ1 ) = λ			0	−3λ x2 = 0,							∂ L(x, λ0 , λ1 ) = 2λ x				2	= 0		;
		∂x1		0		1	1						∂x2		1	2
		∂x1											∂x2
б) g		(x) = x2	− x3 = 0 .
	1	2	1

3.Решим систему для двух случаев.

Впервом случае λ0 = 0 . Тогда λ1 ≠ 0 , так как все множители Лагранжа не могут

быть одновременно равными нулю. Отсюда x = x = 0,

= 0 .

Во втором случае λ0

≠ 0 . Поделим уравнения системы, полученной на втором

шаге, на λ

с заменой

λ1

на λ

λ0

1 −3λ x2

= 0, 2λ x

= 0 ;

− x3

= 0 .

Рассмотрим второе уравнение. Если

λ1 = 0 , то

система несовместна. Если

= 0 , то

= 0

и система тоже

несовместна. Таким образом, применение

классической функции Лагранжа не дает результата.

4. Так как λ0

= 0 , достаточные условия экстремума не проверяются. Точка x

со

значением

целевой

функции

f (x ) = 0

является

точкой нерегулярного

локального и глобального минимума (рис.7.3). ■

132

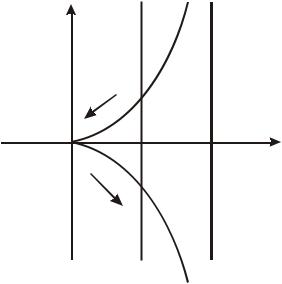
x22 - x13 = 0

f(x) = 0	f(x) = 2
	f(x) = 1

Рис.7.3 Иллюстрация к решению задачи из примера 7.4

Пример 7.5. Найти условный экстремум

f (x) = x12 + x22 → extr, g1 (x) = (x1 −1)2 + x22 − 4 = 0.

□ Будем следовать алгоритму, не проверяя условия регулярности. 1. Составим обобщенную функцию Лагранжа

L(x, λ0 , λ1 ) = λ0 (x12 + x22 ) + λ1 [(x1 −1)2 + x22 − 4].

2. Выпишем необходимые условия экстремума первого порядка

а) ∂L(x, λ0 , λ1 ) = 2λ			0	x + 2λ (x −1) = 0,			∂L(x, λ0 , λ1 ) = 2λ	0	x	2	+ 2λ x	2	= 0	;
	∂x1		0	1	1	1	∂x2	0		2	1	2
	∂x1						∂x2
б) g	(x) = (x −1)2	+ x2			− 4 = 0.
1	1			2

3.Решим систему для двух случаев.

Впервом случае λ0 = 0 . Тогда из п. 2 следует

		2λ1 (x1 −1) = 0,	2λ1 x2 = 0 ,
		(x −1)2 + x2 − 4 = 0.
		1	2
Так как λ0 = 0 , то		λ1 ≠ 0 ; поэтому	из первых двух уравнений x1 =1, x2 = 0 .
Однако при этом ограничение не выполняется:					g1 (x) = −4 ≠ 0,		следовательно
система несовместна.
Во втором случае λ	0	≠ 0 . Поделим уравнения на λ		0	и заменим	λ1	на λ
Во втором случае λ		≠ 0 . Поделим уравнения на λ			и заменим		на λ
						λ0	1
						λ0

133

а) ∂ L(x, λ1 ) = 2x + 2λ (x −1) = 0,																	∂ L(x, λ1 ) = 2x			2	+ 2λ x		2		= 0 ;
		∂x1		1		1	1											∂x2		2		1	2
		∂x1																∂x2
б). g		(x) = (x −1)			2 + x2		− 4 = 0.
	1			1		2
Рассмотрим второе уравнение. Если																	x2 = 0 , то из третьего уравнения следует
x = 3, x = −1				, а из первого				λ	= −				3	,	λ		= −	1	соответственно. Если же λ = −1,											то
x = 3, x = −1				, а из первого				λ	= −					,	λ		= −		соответственно. Если же λ = −1,											то
1	1							1				2				1	2											1
												2					2
первое	уравнение имеет						вид		2 = 0 ,						т.е. система несовместна.												Таким		образом,
найдены две условно-стационарные точки
	A : x			= 3, x	= 0, λ = −				3	;					B :		x = −1, x = 0, λ					= −		1		.
			1	2			1		2								1		2		1		2
									2														2
4. Проверим достаточные условия экстремума
а) d 2 L(x , λ ) = 2(1 + λ )dx								2 + 2(1 + λ )dx2 ;
				1		1	1							1			2
б) d g			(x ) = 2(x		−1)dx + 2x dx						2	= 0;
		1		1		1		2			2
в, г) исследуем точку A . d g1 (A) = 4dx1 + 0 = 0 , откуда dx1 = 0 и
d 2 L( A) = −dx2				− dx2 = −dx		2	< 0 , если							dx		2	≠ 0 .		Поэтому в точке								A	− регулярный
			1	2		2										2
условный максимум.
Исследуем точку B .						d g		(B) = 4dx + 0 = 0 ,											откуда dx		= 0 и d 2 L(B) = dx2								+ dx2	> 0
							1							1						1								1	2
при dx2	≠ 0 . Поэтому в точке B − регулярный условный минимум.
5. Подсчитаем значения функции в точках экстремума																						f ( A) = 9,						f (B) =1. ■
Графическое решение задачи представлено на рис.7.4.
													x2
				f(x) = 9															g1(x) = (x1 - 1)2 + x22 - 4 = 0
				f(x) = 9
							f(x) = 4
														f(x) = 1
																			A 3		x1
							B										1		A 3

Рис. 7.4. Графическое решение задачи из примера 7.5

134

Пример 7.6. Найти условный экстремум в задаче

						f (x) = x2				− x2	→ extr,
									1	2
						g	(x) = x2			+ x2	−1 = 0.
						1			1	2
□ 1. Составим обобщенную функцию Лагранжа
		L(x, λ		0	, λ ) = λ			0	(x2	− x2 ) + λ (x2			+ x2	−1) .
				0		1		0	1	2	1	1	2
2. Запишем необходимые условия экстремума первого порядка
а) ∂L(x, λ0 , λ1 ) = 2λ x + 2λ x = 0,											∂L(x, λ0 , λ1 ) = −2λ				x	2	+ 2λ x	2	= 0	;
	∂x1	0	1		1	1						∂x2		0		2	1	2
	∂x1											∂x2
б) g	(x) = x2	+ x2 −1 = 0.
1	1	2

3.Решим систему для двух случаев.

Впервом случае λ0 = 0 . Тогда λ1 ≠ 0 , поэтому из первых двух уравнений

следует x1 = x2 = 0 . Однако условие "б" при этом не выполняется. Следовательно,

система несовместна.

Во втором случае λ

≠ 0 . Поделим уравнения на λ

и заменим

λ1

на λ

λ0

а) ∂L(x, λ1 ) = 2x (1 + λ ) = 0,

∂ L(x, λ1 ) = 2x

(−1 + λ ) = 0

;

∂x1

∂x2

б) g

(x) = x2

+ x2 −1 = 0.

Пусть λ1

= −1, тогда

x2 = 0,

x1 = ±1. Пусть λ1 =1,

тогда x1

= 0, x2

= ±1. Других

решений система не имеет. Таким образом, имеем четыре условно-стационарные точки

A :	x =1, x		= 0,	λ = −1;	B : x = −1, x = 0, λ			= −1;
	1	2		1	1	2	1
C :	x = 0, x =1,			λ =1;	D : x = 0, x		= −1, λ =1.
	1	2		1	1	2	1

4. Проверим достаточные условия экстремума

а) d 2 L(x , λ ) = 2(1 + λ )dx2 + 2(λ −1)dx2									;
		1		1	1		1	2
б) d g	(x ) = 2x dx + 2x dx					2	= 0;
1		1	1		2	2
в, г) исследуем точку A .						d g1 (A) = 2dx1			= 0 , откуда получаем dx1 = 0 и
d 2 L( A) = −4dx22		< 0 ,	если		dx2		≠ 0 . Поэтому в точке A − регулярный			локальный
условный максимум.
Исследуем точку B .					d g	(B) = −2dx		= 0 , откуда dx = 0 и d 2 L(B) = −4dx2			< 0 при
					1		1		1	2

dx2 ≠ 0 . Поэтому в точке B − регулярный локальный условный максимум.

135

Исследуем точку

C . d g

= 0 ,

откуда dx

= 0

и d 2 L(C) = 4dx2

> 0

при

dx1

≠ 0 . Поэтому в точке C − регулярный локальный условный минимум.

Исследуем точку D . d g

(D) = −2dx

= 0

, откуда dx

= 0

и d 2 L(D) = 4dx

> 0

при

dx1

≠ 0 . Поэтому в точке D − регулярный локальный условный минимум.

5. Вычислим

значения

функции

в точках

условного экстремума

f ( A) = f (B) =1; f (C) = f (D) = −1. ■

Графическое решение задачи представлено на рис. 7.5.

f(x) = - 1

f(x) = 1

g1(x) = 0

f(x) = - 1

Рис.7.5. Графическое решение задачи из примера 7.6

Пример 7.7. Найти условный экстремум в задаче

f (x) = 12 [(x1 −1)2 + x22 ]→ extr, g1 (x) = −x1 +α x22 = 0

при различных α > 0 .

□ Проверим условие регулярности. Так как g1 (x) = (−1, 2α x2 )T ≠ 0 ни в одной точке множества U , то условие выполняется. Поэтому воспользуемся классической функцией Лагранжа.

1. Составим функцию Лагранжа

L(x, λ1 ) = 12 [(x1 −1)2 + x22 ]+ λ1 (−x1 +α x22 ) .

2. Запишем необходимые условия экстремума первого порядка

136

а) ∂L(x, λ1 ) = x −1 −λ = 0,

∂L(x, λ1 ) = x

+ 2αλ x

= 0;

∂x1

∂x2

б) g

(x) = −x +α x2 = 0 .

3. Из второго уравнения следует x2 (1 + 2αλ1 ) = 0 . Если x2

= 0 , то x1

= 0 , а λ1 = −1.

Если λ

= −

, то x

=1 +

=1 −

2α −1

и при этом

= ± 2α −1 .

2α

2α2

При 0 < α <

решения

не

существует. Таким образом,

имеются

три условно-

стационарные точки (рис.7.6)

A : x1 = 0, x2 = 0, λ1 = −1;

B : x = 2α −1		,	x	2	= 2α −1,	λ = − 1			;
1	2α			2	2α2	1		2α
	2α				2α2			2α
C : x = 2α −1		,	x	2	= − 2α −1,	λ = − 1 .
1	2α			2	2α2		1	2α
	2α				2α2			2α

4. Проверим достаточные условия экстремума

а) d 2 L(x , λ ) = dx2			+ (1 + 2αλ )dx2				;
	1	1			1	2
б) d g	(x ) = −dx + 2αx dx			2	= 0;
1		1	2	2
x2			1				α = 1
		α = 4

f(A) = 12

A	1	1
	2

f(B) = f(C) = 4α - 1 8α2

1	α = 1
α = 4

Рис.7.6. Иллюстрация к решению задачи из примера 7.7

137

в) выразим из последнего пункта d x :

= 2αx dx

;

г) d

2 L(x , λ ) = ((4αx )2 + (1 + 2αλ ))dx2 .

Исследуем точку A . d 2 L(x , λ ) = (1 − 2α)dx2 .

При 0 < α <

получаем, что d 2 L(x

, λ ) > 0

при dx

≠ 0 и в точке A − условный

локальный минимум.

При α >

находим, что

d 2 L(x , λ ) < 0 при

≠ 0 и в точке

A –

условный

локальный максимум.

При

α =

получаем,

что d 2 L(x , λ ) = 0

при

любых dx

требуется

дополнительное исследование.

Для этого воспользуемся методом исключения переменных. Выразим из

уравнения

ограничения

одну

из координат

Подставим полученное

выражение в целевую функцию

. Исследуем

f (x) =

(

x2 −1)

+ x2

x2 +

полученную функцию на безусловный экстремум.

x23

+ x2

= 0 ,

отсюда x2 = 0

dx2

− стационарная точка.

В этой точке

первая

отличная

от

нуля

производная

f (4) (x ) = 3 > 0

является четной и положительной. Следовательно,

в точке x2 −

локальный

минимум. С

учетом связи

)2 = 0

получаем,

что

в точке

x = (0, 0)T

− условный локальный минимум.

Рассмотрим точки B и C . d 2 L(x , λ ) =16α 2

2α −1

dx2

= 8(2α −1)dx2 .

2α

При α

имеем x

= x = 0

и d 2 L(x , λ ) = 0

при всех

Значит,

требуется

дополнительное исследование, которое уже было выполнено.

При α > 12 имеем d 2 L(x , λ1 ) > 0 при dx2 ≠ 0 и в точках B и C условный

локальный минимум.
5. Значение функции в точках экстремума f ( A) =	1	,	f (B) = f (C) =	4α −1	. ■
	2			8α 2

Иллюстрация к решению задачи представлена на рис. 7.6.

138

<<< < Предыдущая 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 2526 / 3326 27 28 29 30 31 32 33 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
27.03.201629.56 Кб28Кейс 4.docx
#
25.09.20192.02 Mб20КиД.doc
#
26.04.2019510.84 Кб29КиСА Экзамен.docx
#
27.03.201612.16 Mб33Клюшин Введение в дискретку.djvu
#
05.06.20151.16 Mб84книга по английскому.doc
#
05.06.201512.36 Mб554Книга_МО.pdf
#
05.06.2015420.05 Кб6колбок по линалу.pdf
#
18.11.20191.15 Mб5Колл.doc
#
05.06.201591.48 Кб69коллоквиум по химии вопросы 1-15.docx
#
05.06.201527.65 Кб67Коллоквиум Химия.doc
#
05.06.20151.17 Mб29Командообразование ДЗ1.docx