процедуру. При этом градиент вычисляется гораздо реже, поскольку это происходит только при смене направлений движения.

5.4. Метод наискорейшего спуска

Данный метод является вариантом градиентного спуска. Здесь также полагают pk = − f (xk ), но величина шага αk из (5.11) находится в результате решения задачи одномерной оптимизации

Следует отметить, что решение задачи (5.13) можно получить одним из рассмотренных для одномерной минимизации способов. Если, кроме того, функция

наискорейшего спуска для решения задачи ее минимизации из начальной точки

Величину шага исчерпывающего спуска αk найдем по формуле для квадратичной функции. Результаты вычислений приведены в табл. 5.1.

83

Результаты вычислений задачи методом наискорейшего спуска Таблица 5.1

Полученные результаты можно сравнить с решением этой же задачи методом градиентного спуска. ■

Отметим главный недостаток градиентных методов, который заключается в неприемлемо низкой скорости сходимости в случаях, когда поверхности уровня целевой функции сильно "вытянуты", т.е. имеют овражный характер. Геометрически происходит следующее: генерируемые методом приближения быстро спускаются почти на "дно оврага", а затем начинают "прыгать" с одного его "склона" на другой, причем длина осуществляемых шагов все время уменьшается. Особенно сильный замедляющий эффект это явление оказывает в том случае, когда "дно оврага" изогнуто.

В следующих разделах главы будут рассмотрены методы, обладающие высокой скоростью сходимости и значительно менее чувствительные к овражному характеру целевой функции задачи.

Рассмотрим один важный класс методов, который не требует информации о вторых производных целевой функции, как метод Ньютона, однако обладает более высокой скоростью сходимости, чем градиентные методы. Повышение скорости сходимости здесь не связано с существенным ростом трудоемкости итерации, а обусловлено идей, лежащей в основе метода.

5.5. Метод сопряженных направлений

Этот итерационный метод, предназначенный для отыскания минимума выпуклой квадратичной функции, приводит к результату за конечное число шагов. От такого метода разумно ожидать высокой эффективности и в случае выпуклой неквадратичной функции.

84

Разберем идею метода на примере поиска минимума в случае функции двух переменных. Линиями уровня сильно выпуклой квадратичной функции являются эллипсы. Пусть p1 , p2 − направления главных осей этих эллипсов (они могут быть

из условия исчерпывающего спуска, то, очевидно, потребуется не более двух шагов для отыскания точки x .

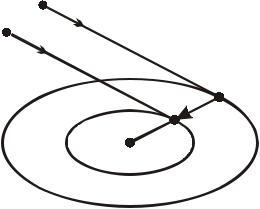
Такого же результата можно достичь и другим способом. Выберем некоторое направление p1 и две точки x0 и y0 такие, что векторы x0 − y0 и p1 были неколлинеарны. Выполнив исчерпывающий спуск из точек x0 и y0 в направлении

p1 , получим точки x1 и y1 . По свойству исчерпывающего спуска в точках x1 и y1

имеет место касание соответствующих прямых (направлений убывания) и эллипсов

(линий уровня целевой функции). По свойству эллипсов, точки x , x1 и y1

расположены на одной прямой. Поэтому, полагая p2 = x1 − y1 , и решая задачу f (x1 +α p2 ) → min , мы находим точку x . Таким образом, и в этом случае решение задачи минимизации сильно выпуклой квадратичной функции будет получено за конечное число шагов.

y0 p1

x0

p1

y1

x1 p2

x*

p2 = x1 - y1

Рис. 5.3. Определение направления p2 и положение точки x в E2

Рассмотренному на примере квадратичной функции двух переменных методу может соответствовать такой алгоритм.

Шаг 1. Выбрать начальную точку x0 E2 . Перейти к шагу 2.

85

вычисления закончить, положив x = x2 .

Графическая иллюстрация работы алгоритма представлена на рис. 5.4. Поиск точки минимума проводится по так называемым сопряженным направлениям.

x2

86

положительно определенной матрицы A , линейно независима.

□ Предположим противное, т.е. что существует линейная комбинация, равная нулю

Утверждение. Если в итерационном процессе (5.16) на каждом шаге

□ Раскрывая рекуррентную формулу (5.16), получаем

Из формулы (5.18), учитывая выражение для градиента квадратичной функцииf (x) = Ax + b , находим

87