
- •Аннотация
- •Оглавление
- •Предисловие
- •ГЛАВА 1. Задачи оптимизации. Основные определения
- •1.1. Задачи оптимизации
- •1.2. Минимум функции одной переменной
- •1.3. Унимодальные функции
- •1.4. Выпуклые функции
- •1.5. Условие Липшица
- •1.6. Классическая минимизация функции одной переменной
- •Вопросы и задания для самоконтроля
- •ГЛАВА 2. Одномерная минимизация функций. Прямые методы
- •2.1. О прямых методах
- •2.2. Метод перебора
- •2.3. Метод поразрядного поиска
- •2.4. Метод дихотомии
- •2.5. Метод золотого сечения
- •2.6. Сравнение методов перебора, дихотомии и золотого сечения
- •2.7. Метод парабол
- •Вопросы и задания для самоконтроля
- •Задание для численной реализации в среде программирования MATLAB
- •ГЛАВА 3. Одномерная минимизация. Методы, использующие информацию о производных целевой функции
- •3.1. Метод средней точки
- •3.2. Метод хорд
- •3.3. Метод Ньютона
- •3.4. Возможные модификации метода Ньютона
- •3.5. Методы минимизации многомодальных функций
- •Вопросы и задания для самоконтроля
- •Задание для численной реализации в среде программирования MATLAB
- •ГЛАВА 4. Задача минимизации функции многих переменных. Необходимые и достаточные условия безусловного экстремума
- •4.1. Постановка задачи и определения
- •4.2. Свойства выпуклых множеств и выпуклых функций
- •4.3. Необходимые и достаточные условия безусловного экстремума
- •Вопросы и задания для самоконтроля
- •5.1. Выпуклые квадратичные функции
- •5.2. Общие принципы многомерной минимизации
- •5.3. Метод градиентного спуска
- •5.4. Метод наискорейшего спуска
- •5.5. Метод сопряженных направлений
- •5.6. Метод сопряженных градиентов
- •5.7. Метод Ньютона
- •5.8. Квазиньютоновские методы
- •Вопросы и задания для самопроверки
- •Задание для численной реализации в среде программирования MATLAB
- •ГЛАВА 6. Прямые методы безусловной минимизации многомерных задач
- •6.1. Проблема минимизации многомерных задач
- •6.2. Минимизация функций по правильному (регулярному) симплексу
- •6.3. Минимизация функций при помощи нерегулярного симплекса
- •6.4. Метод циклического покоординатного спуска
- •6.5. Метод Хука–Дживса
- •6.6. Методы случайного поиска
- •Вопросы и задания для самопроверки
- •Задание для численной реализации в среде программирования MATLAB
- •7.1. Условный экстремум при ограничениях типа равенств
- •7.2. Условный экстремум при ограничениях типа неравенств
- •Вопросы и задания для самопроверки
- •ГЛАВА 8. Линейное программирование
- •8.1. Определения. Примеры задач линейного программирования
- •8.2. Общая и каноническая задачи линейного программирования
- •8.3. Геометрическое истолкование задач линейного программирования
- •8.4. Аналитическое решение задач линейного программирования
- •Вопросы и задания для самоконтроля
- •Литература
выпуклых функций, так как в достаточно малой окрестности точки минимума x дважды дифференцируемая функция f (x) с положительно определенной матрицей Гессе H (x) хорошо аппроксимируется сильно выпуклой квадратичной функцией.
5.2. Общие принципы многомерной минимизации |
|
Для численного решения задач безусловной минимизации f (x) → min , |
x En |
разработано много алгоритмов, использующих итерационные процедуры вида |
|
xk +1 = Φ(xk , xk −1 , ..., x0 ) , x0 En . |
(5.3) |
Эти алгоритмы позволяют при определенных условиях построить последовательность {xk }такую, что
lim f (xk ) = f = min |
f (x), если U ≠ Ø |
|
(5.4а) |
|||
k →∞ |
|
En |
|
|
|
(5.4б) |
lim f (xk ) = f = inf |
f (x), если U = Ø |
|
||||
k →∞ |
|
En |
|
|
|
|
где U − множество |
точек |
глобального |
минимума |
функции |
f (x) . |
|
Последовательность |
{xk }, |
удовлетворяющая |
требованию |
(5.4), называется |
||
минимизирующей для |
функции f (x) . Если, кроме того, для случая |
U ≠ Ø |
||||
дополнительно выполняется условие |
|
|
|
|
||
|
lim ρ (xk , U ) = 0 , |
|
|
(5.5) |
||
|
k |
→∞ |
|
|
|
|
то говорят, что минимизирующая последовательность сходится к множеству U . |
||||||
Если множество U состоит из единственной точки |
x , то для сходящейся к U |
||||||
минимизирующей последовательности lim xk = x . |
|
|
|
|
|||
|
k→∞ |
|
|
|
|
|
|
|
Необходимо отметить, что |
|
|
|
|
|
|
|
1. ρ (x, U ) = inf ρ(x, y) есть расстояние от точки x до множества U . |
||||||
|
y U |
|
|
|
|
|
|
|
2. Минимизирующая последовательность может и не |
сходиться к точке |
|||||
минимума. Например, для функции |
f (x) = |
x2 |
, |
x E , |
последовательность |
||
|
|||||||
|
|
|
1 + x4 |
|
1 |
|
|
|
|
|
|
|
|
|
|
xk |
= k является минимизирующей, но не сходится к единственной точке минимума |
||||||
x |
= 0 . Напротив, минимизирующая последовательность xk =1/ k |
сходится к точке |
|||||
минимума x = 0 . |
|
|
|
|
|
|
|
|
Вопрос о существовании точки минимума обычно решается с помощью |
||||||
теоремы Вейерштрасса: если функция |
f (x) |
непрерывна |
в |
En и множество |
|||
75

U α = {x : f (x) ≤α} для некоторого α непусто и ограничено, то f (x) достигает
глобального минимума в En .
Важной характеристикой сходящихся минимизирующих последовательностей является скорость сходимости. Последовательность {xk } сходится к точке x
линейно (со скоростью геометрической прогрессии), если существует такое число
q (0, 1) , |
что |
выполняется |
неравенство |
ρ (xk , x ) ≤ q ρ (xk −1 , x ) , |
т.е. |
|||
ρ (xk , x ) ≤ qk ρ (x0 , x ) . |
|
|
|
|
|
|
||
Сходимость |
называется сверхлинейной, если |
ρ (xk , x ) ≤ qk ρ (xk −1 , x ) , и |
||||||
qk → +0 при k → ∞. |
|
|
|
|
|
|
||
Наконец, |
термин |
квадратичная |
сходимость |
используется, |
если |
|||
ρ (xk , x ) ≤ [cρ(xk −1 , x )]2 , c > 0 .
Установление сходимости последовательности {xk } из (5.5) и оценка скорости сходимости дают существенную информацию об итерационном процессе. Конкретный вычислительный алгоритм на основе (5.3), в котором может получаться, вообще говоря, бесконечная последовательность {xk }, необходимо
дополнять критерием окончания итерационного процесса. На практике используются следующие условия прекращения итераций
ρ (xk +1 , xk ) < ε1
|
f (xk +1 ) − f (xk ) |
< ε2 |
(5.6) |
||
|
f (xk ) |
|
< ε3 |
||
|
|
|
|||
где εi − заранее заданные параметры точности.
Далее будут рассмотрено несколько двухслойных вычислительных алгоритмов, основанных на рекуррентных формулах вида
|
|
xk +1 = xk +αk |
pk , k = 0, 1, ... , |
|
|
(5.7) |
где вектор |
pk − направление поиска из точки |
xk в точку xk +1 , |
а число αk − |
|||
величина |
шага, |
которая |
выбирается |
так, |
чтобы |
выполнялось |
условие f (xk +1 ) < f (xk ) . Эти алгоритмы будут различаться способом построения вектора pk и выбора шага αk .
76
Определение. В итерационном процессе (5.7) производится исчерпывающий спуск, если величина шага αk находится из решения одномерной задачи минимизации
Φ |
α |
→ |
min , |
Φ |
α |
= |
f (x |
k +α |
p |
k |
) . |
(5.8) |
|
k ( ) |
|
|
k ( ) |
|
|
|
|
||||
|
|
|
α |
|
|
|
|
|
|
|
|
|
Таким образом, при исчерпывающем спуске на каждом шаге полностью
реализуется возможность уменьшить значение целевой функции |
f (x) при |
|
перемещении из точки |
xk в направлении, коллинеарном вектору pk . |
Величина |
шага αk может быть |
найдена с помощью рассмотренных ранее |
методов |
одномерной минимизации. В дальнейшем будет использоваться следующее важное свойство исчерпывающего спуска.
Теорема. Если функция |
f (x) |
дифференцируема |
в En , то в |
итерационном |
|||||
процессе (5.7) с выбором шага с исчерпывающим |
спуском для |
любого k ≥1 |
|||||||
выполняется условие |
|
|
|
|
|
|
|
|
|
|
f (x |
k +1 |
), p |
k |
) |
= |
0 . |
|
(5.9) |
( |
|
|
|
|
|
||||
□ Запишем необходимое условие минимума функции одной переменной Φk (α)
из (5.8), используя правило дифференцирования сложной функции
|
d Φk (α) |
n |
∂ f (xk +1 ) d xkj +1 |
|
|
|||||
|
|
|
= ∑ |
|
|
|
|
= 0 . |
||
|
d α |
∂ x j |
|
d α |
||||||
|
j=1 |
|
|
|
||||||
|
|
|
|
|
d xk +1 |
|
|
|
||
Учитывая, что xkj +1 = xkj +α pkj |
, поэтому |
|
j |
= pkj |
. Отсюда получаем условие |
|||||
dα |
||||||||||
|
|
|
|
|
|
|
|
|||
(5.9). ■ |
|
|
|
|
|
|
|
|||
Геометрическая иллюстрация |
соотношения |
(5.9) |
в E2 выглядит так. При |
|||||||
перемещении из точки xk вдоль прямой, задаваемой вектором pk в направлении
убывания функции, |
происходит пересечение линий уровня функции f (x) . Это |
|||
происходит до тех |
пор, пока |
либо не |
будет достигнута стационарная |
точка |
( f (xk +1 ) = 0 ), либо |
прямая не |
коснется |
в точке xk +1 некоторой линии |
уровня |
функции f (x) . Равенство (5.9) и есть условие касания (рис.5.1).
77
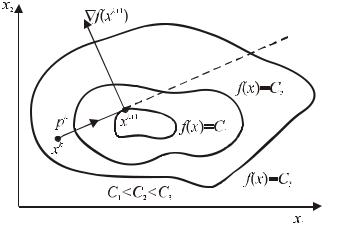
Рис. 5.1. Ортогональность направления pk градиенту f (xk +1 ) при исчерпывающем спуске
Свойство |
( f (xk +1 ), pk ) = 0 позволяет в явном виде найти величину α k |
для |
|||||||||||
квадратичной функции. |
|
|
|
|
|
|
|
|
|
|
|
|
|
Теорема. |
Для квадратичной функции |
f (x) = |
1 |
(A x, x) + (b, x) + c величина |
αk |
||||||||
|
|||||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
исчерпывающего спуска в итерационном процессе xk +1 = xk +αk pk , |
k = 0, 1, ... равна |
||||||||||||
|
αk = − |
( f (xk ), pk ) |
|
= − |
(Axk + b, pk ) |
. |
|
(5.10) |
|||||
|
|
(Apk , pk ) |
(Apk , pk ) |
|
|
|
|||||||
|
|
|
|
|
|
|
|
||||||
□ Действительно, умножив равенство |
xk +1 = xk +αk pk слева |
на |
матрицу |
A |
|||||||||
квадратичной |
функции |
|
f (x) и прибавив |
к обеим частям вектор |
b , получим |
||||||||
Axk +1 + b = Ax k |
+ b +αk Ap k . |
Учитывая, |
что градиент квадратичной функции равен |
||||||||||
f (x) = Ax + b , имеем f (xk +1 ) = f (xk ) +αk Ap k . Подставляя выражение для f (xk +1 )
в равенство ( f (xk +1 ), pk ) = 0 , получаем формулу (5.10). ■
Определение. Направление вектора pk называется направлением убывания
функции f (x) в точке xk , если при всех достаточно малых положительных α выполняется неравенство f (xk +α pk ) < f (xk ) .
В итерационном процессе используются, как правило, направления убывания. Сформулируем признак направления убывания.
Теорема (достаточное условие направления убывания). Пусть функция
дифференцируема в точке xk . Если |
вектор pk удовлетворяет условию |
( f (xk ), pk ) < 0 , то направление вектора pk |
является направлением убывания. |
|
78 |
