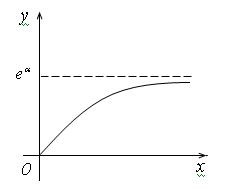
32

Рисунок 3.4

Модели 3.14 и 3.17 сводятся к линейной форме путем перехода от уровней переменных к их логарифмам или обратным величинам.

3.2. Итерационные методы подбора нелинейных моделей

то есть имеет аддитивные ошибки.

В этой модели взятие логарифмов от обеих частей не приводит к линейной модели наблюдений.

Для получения оценок наименьших квадратов параметров α и β сумму квадратов

i=1

минимизируют, используя итерационные методы, в процессе реализации которых, сначала задаются некоторые «стартовые значения» оцениваемых параметров, а затем производится последовательное приближение значений (а и b) оценок параметров α и β, минимизирующих Q (a, b).

3.3. Нелинейные модели множественной регрессии

Ранее нами рассматривались примеры некоторых регрессионных моделей с двумя переменными, приводимых к линейной форме путем логарифмирования или замены переменной. Регрессионные модели с числом переменных более двух называются моделями множественной регрессии. Приведем перечень нелинейных моделей множественной регрессии, линеаризуемых перечисленными методами:

33

1. Степенная модель с мультипликативными возмущениями

34

x1 x2 = x' ,…, тогда

После преобразования перечисленных моделей к линейной форме их параметры и качество оцениваются с помощью методов, применяемых для линейных множественных регрессионных моделей, рассмотренных ниже.

Степенная модель с аддитивными возмущениями

не может быть приведена к линейной форме. Для оценки ее параметров используются итерационные методы подбора нелинейных моделей.

3.4. Проверка статистических гипотез о значениях отдельных коэффициентов

Ранее мы говорили о способе построения доверительного интервала на уровне значимости α

.

значения, взятого значения β0 представляет осуществление редкого события, имеющего малую вероятность, и это дает нам основание сомневаться в том, что значение параметра β = β0

35

Априорные предположения о значениях параметров модели называют статистическими гипотезами.

О проверяемой гипотезе говорят как об исходной «нулевой» гипотезе и обозначают ее Но, в нашем случае Но: β = β0 .

В соответствии со сказанным выше, такую гипотезу следует отвергать, если значение β0 не

принадлежит (1−α) -процентному доверительному интервалу. β0 не будет принадлежать этому интервалу в том случае, если наблюдаемое значение отношения больше табличного по абсолютной величине

параметра β в сравнении с оценкой Sb стандартного отклонения этого параметра.

Правило решения вопроса об отклонении или не отклонении статистической гипотезы Но, называется статистическим критерием проверки гипотезы Но, а выбранное при формулировании этого правила значение α называется уровнем значимости критерия.

В практических исследованиях чаще всего используют, α = 0,05 хотя иногда и α =0,01 , α = 0,1 и другие. Выбор большего или меньшего значения α определяется степенью значимости для исследования исходной гипотезы Но. Если мы выбираем при исследовании меньшее значение α , то мы уменьшаем вероятность ошибки и вероятность отвержения верной гипотезы. Такие вероятности называют мощностью критерия.

В реальных ситуациях статистические критерии имеют довольно низкую мощность, так что рассматриваемая Но отвергается редко, поэтому правильнее говорить о не отвержении гипотезы, а не о ее принятии.

Всякий статистический критерий основывается на использовании той или иной статистики, то есть, случайной величины, значения которой могут быть вычислены теоретически на основании имеющихся статистических данных (приближенно).

В нашем случае критерий проверки гипотезы Но: β = β0 основан на использовании t-

статистики b − β0 , значение которой можно вычислить по

Sb

данным наблюдений. Критерии, основанные на использовании t-статистики (распределения) Стьюдента называют t-критериями. Каждому статистическому критерию соответствует критическое множество R значений статистики критерия, при которых гипотеза Но отвергается в соответствии с принятыми правилами (то есть множество значений t-статистики, превышающих по абсолютной

величине t1−α;n−m ).