Файловый архив студентов. Файловый архив студентов.
1261 вуз, 4614 предмет.
/ Регистрация
FAQ Обратная связь Вопросы и предложения
Добавил:
Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Тольяттинский государственный университет
Предмет:
[НЕСОРТИРОВАННОЕ]
Файл:
эконометрика.pdf
Скачиваний:
178
Добавлен:
28.05.2015
Размер:
639.74 Кб
Скачать
☆
►Содержание►

27

3.Нелинейные регрессионные модели

3.1.Нелинейные модели с двумя переменными, приводимые к линейной форме

3.1.1.Степенная форма эконометрической модели

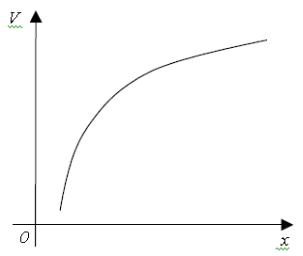
Связь между конкретными экономическими факторами не обязательно линейная. Например, если рассматривать зависимость от располагаемого дохода x не всех затрат на личное потребление у, а лишь затрат V на некоторый продукт питания (или группу продуктов питания), например, на куриные яйца, то уже по чисто физиологическим причинам функция связи V=V(x) скорее всего должна замедлять свой рост при возрастании x. Возможный график этой функции имеет вид, приведенный на рис. 3.1.

Рисунок 3.1

В данной ситуации нельзя говорить о склонности к потреблению данного продукта как о постоянной величине. Вводят понятие предельной склонности к потреблению.

Определение. Предельной склонностью к потреблению (нормой потребления) называют величину C(x), которая для заданной величины располагаемого дохода х определяется формулой

C(x) = lim

V (x + x) −V (x)

=

dV

′

(3.1)

x

dx

=V (x)

x→0

 

 

 

28

Замедление скорости роста функции V(x) соответствует убыванию С(х) при возрастании располагаемого дохода х. Уточняя предположение о поведении нормы потребления С(х), можно получить ту или иную формулу связи между переменными V и х.

Возможной формой связи затрат V на некоторый продукт питания от располагаемого дохода х может быть степенная связь

V =V (x) = α × x β

(3.2)

где α > 0 , 0 < β <1.

 

 

Для такой связи производная (норма

потребления) C(x) =α × β × xβ −1 , то есть

эта склонность к потреблению монотонно убывает с ростом располагаемого дохода х.

3.1.2. Приведение степенной модели к линейной форме модели, оценка параметров модели и ее качества

Если вместо уровней дохода и расходов на потребления рассмотреть логарифмы уровней по одному и тому же основанию (натуральные или десятичные log) , то степенную форму связи можно привести к линейной.

V = α × xβ ® lnV = lnαxβ .

lnV = lnα +ln xβ

 

lnV = lnα + β ln x .

(3.3)

Если обозначить lnV = V ′ , lnα = α ′ , ln x = x′, то получим

 

V ′ = α ′ + β × x′

(3.4)

Линейной форме модели в логарифмах соответствует линейная модель наблюдений

Vi′= α ′ + βxi′ + εi i = 1,2,...,n,,

(3.5)

β = d(ln V )

где d(ln x) .

Модель yi = α × xiβ ×εi , линеаризуемая путем логарифмирования называется степенной моделью с мультипликативными возмущениями.

Оценить параметры такой модели можно с помощью МНК, применив данный метод к уравнению (3.3) и далее перейдя от логарифмов к исходным показателям. Качество непосредственно степенной модели (3.2) оценивают графическим методом (сравнивая облако рассеяния с полученной по теоретической модели кривой), с помощью средней ошибки аппроксимации и коэффициента детерминации. Соблюдение стандартных предположений регрессионного анализа проще всего проследить, используя графики стандартизированных остатков (см. §2.5). О качестве исходной модели (3.2) также можно судить по модели (3.3), применив методы, изложенные в главе 2.

3.1.3. Понятие предельной склонности и эластичности функции

Определение. Если имеется связь между какими-то

переменными экономическими

факторами х и у в виде Y = f (x) то функция

 

 

dy

 

′

y(x + x) − y(x)

C(x) =

 

= f

(x) = lim

 

dx

x

 

 

x→0

является предельной склонностью величины y по отношению к величине х.

Определение. Величина

 

 

 

 

 

 

 

 

 

 

f (x +

 

x) − f (x)

×100%

 

 

 

 

η(x) = lim

 

 

f (x)

==

x

× dy

,

 

 

 

 

Dx

 

y

x→0

 

 

 

dx

 

 

 

 

 

 

×100%

 

 

 

 

 

 

 

 

 

x

 

 

 

 

 

η(x) = xy C(x)

29

(3.6)

(3.7)

(3.8)

в экономической теории называется эластичностью (функцией эластичности).

Эластичность показывает, на какое количество процентов изменится у при изменении x на

1%.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Если

 

η(x)

 

>1то фактор у эластичен по отношению к фактору х.

 

 

 

 

 

 

Если же

 

η(x)

 

<1,

то фактор y неэластичен по отношению к фактору х. Отдельно

 

 

выделяют пограничные случаи η(x) =±1.

 

 

 

 

 

 

Найдем отношение дифференциалов для логарифмов уровней факторов у и х.

 

 

 

 

 

 

 

 

 

 

 

 

df (x)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

d ln f (x)

=

f (x)

 

x dy

=η(x)

 

 

 

 

 

 

 

 

 

 

 

d ln x

dx

= y dx

(3.9)

 

 

 

 

 

 

 

 

 

 

 

x

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Значение

 

предельной

склонности

С(x0 )

равно

угловому

коэффициенту

наклона

касательной к графику функции

y = f (x) при x = x0

 

 

 

Значение

эластичности

η(x0 ) равно

угловому коэффициенту

касательной к

графику

зависимости ln y от ln x при x = x0

Следствие:

1. Условие постоянства предельной склонности С(x) = β означает линейную связь между

уровнями факторов х и у:

 

y =α + βx

(3.10)

2. Условие постоянства эластичности η(x) = β означает

линейную связь между

логарифмами уровней

 

ln y =α′ + β ln x ,

(3.11)

30

соответствующую степенной связи между уровнями факторов. Преобразовав выражение (3.11) можно получить формулу (3.2):

 

 

eln y = e(α ′+β ln x) ,

 

 

y = eα ′ (eln x )β

®

y = eα ′ × xβ

®

y = αxβ

(α = eα′ ) .

Выражает степенное возрастание (при β > 0 ) или убывание (при β < 0 ) уровней фактора у при возрастании уровней фактора x.

Если η(x) = β , то коэфицент β можно трактовать как процентное изменение уровня фактора у при изменении фактора х на 1%.

Если β >1, то фактор y эластичен по отношению к фактору х. Если β <1 , то фактор y не эластичен по отношению к фактору х.

Пограничные случаи, когда β =±1 соответствуют единичной эластичности.

3.1.4. Другие виды эконометрических моделей, приводимые к линейной форме

Если у – объем плановых инвестиций, a z – норма банковского процента, то между ними существует связь (рис. 3.2), которая часто выражается в форме обратно пропорциональной зависимости:

y = α + β

(α > 0, β > 0) .

z

 

Эта модель приводится к линейной, заменой переменной x = 1z : y =α +βx .

Рисунок 3.2

В этой модели эластичность у по z отрицательна и меньше единицы величине

η(z) = dy ×

z

= -

β

×

 

z

 

= -

β

,

 

z2

 

 

β

β +αz

dz y

 

 

α +

 

 

 

 

 

 

 

z

 

 

 

(3.12)

по абсолютной

(3.13)

следовательно объем плановых инвестиций неэластичен по отношению к норме процента (проценты растут быстрее, чем инвестиции).

31

В моделях «доход-потребление», относящихся к потреблению продуктов питания линейная модель в логарифмах уровней, выражающая уменьшение нормы потребления C(x) с ростом доходов х, не всегда удовлетворительна, поскольку эластичность в такой модели η = const . 0

Часто более подходящей является модель связи с убывающей эластичностью (рис. 3.3). Например:

y =α + β ln z

(3.14)

Тогда

η(z) = dy

×

z

 

=

β

×

 

z

 

;

y

z

α + β ln z

dz

 

 

 

 

 

lim(z) = lim

 

 

 

 

β

= 0.

 

 

 

 

 

 

 

 

z→∞

z→∞ (α + β ln z)

 

 

(3.15)

(3.16)

Рисунок 3.3

В этой модели возникают проблемы с отрицательными значениями у при малых значениях z. Такого недостатка нет в модели

ln y = α −

β

 

(β >0) ,

 

 

 

 

 

z

 

 

 

 

 

то есть

 

 

 

 

 

 

 

 

 

 

y =e

(α−β )

.

 

 

 

 

z

 

 

 

 

 

 

 

 

 

 

Здесь

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

β

 

 

η(z) = dy

×

z

= e(α − z

)

* β * z ,

y

 

dz

 

 

 

 

 

2

e

(α − β )

 

 

 

 

 

 

 

z

 

 

 

 

 

 

z

 

η(z) = βz .

(3.17)

(3.18)

(3.19)

Последнее соотношение выражает закон Энгеля – убывания эластичности потребления продуктов питания по доходу. Значения у в этой модели ограничены сверху значением eα .

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
Помощь Обратная связь Вопросы и предложения Пользовательское соглашение Политика конфиденциальности