Файловый архив студентов. Файловый архив студентов.
1261 вуз, 4614 предмет.
/ Регистрация
FAQ Обратная связь Вопросы и предложения
Добавил:
Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Тольяттинский государственный университет
Предмет:
[НЕСОРТИРОВАННОЕ]
Файл:
эконометрика.pdf
Скачиваний:
178
Добавлен:
28.05.2015
Размер:
639.74 Кб
Скачать
☆
►Содержание►

 

 

 

 

 

 

 

 

 

 

 

 

 

42

Где

bi

–

коэффициент регрессии для фактора

xi

в уравнении

множественной регрессии,

$yx ×x ,x

,...x

 

,x

,...,x

– частное уравнение регрессии.

 

 

 

 

 

i 1

2

i −1

i +1

m

 

 

 

 

 

 

 

Наряду с частными коэффициентами эластичности могут быть найдены средние по

совокупности показатели эластичности:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

xi

 

 

 

 

 

 

 

 

 

Эi =bi ×

 

,

(4.11)

 

 

 

 

 

 

 

yx

 

 

 

 

 

 

 

 

 

 

 

i

 

 

 

которые показывают на сколько процентов в среднем изменится результат, при изменении соответствующего фактора на 1%. Средние показатели эластичности можно сравнивать друг с другом и соответственно ранжировать факторы по силе их воздействия на результат.

4.3.Проверка значимости уравнения множественной линейной регрессии

4.3.1.Коэффициенты множественной корреляции и детерминации

Коэффициент множественной корреляции характеризует тесноту линейной связи рассматриваемого набора факторов с исследуемым признаком или, иначе, оценивает тесноту совместного влияния факторов на результат.

Независимо от формы связи коэффициент множественной корреляции может быть найден следующим образом:

S 2

Ryx1x2 ... xm = 1− Sε2i (4.12)

y

где S y2 – оценка общей дисперсии результативного признака; Sε2i – оценка остаточной дисперсии. Границы изменения индекса множественной корреляции от 0 до 1. Чем ближе его значение к

1, тем теснее связь результативного признака со всем набором исследуемых факторов. Величина коэффициента множественной корреляции должна быть больше или равна максимальному парному коэффициенту корреляции:

Ryx x ...x

³ ryx (max) (i =

 

) .

 

1,m

(4.13)

1 2 m

i

 

При правильном включении факторов в регрессионную модель величина коэффициента множественной корреляции будет существенно отличаться от коэффициента корреляции парной зависимости. Если же дополнительно включенные в уравнение множественной регрессии факторы третьестепенны, то коэффициент множественной корреляции может практически совпадать с коэффициентом парной корреляции (различия в третьем, четвертом знаках). Отсюда ясно, что сравнивая коэффициенты множественной и парной корреляции, можно сделать вывод о целесообразности включения в уравнение регрессии того или иного фактора.

Расчет коэффициента множественной корреляции предполагает определение уравнения множественной регрессии и на его основе остаточной дисперсии:

43

2

 

1

ˆ

 

 

 

 

2

 

Sε

=

n

å(yi − yx1x2 ... xm ) .

(4.14)

i

 

 

Можно пользоваться следующей формулой коэффициента множественной детерминации:

R

2

= 1−

å(yi − yˆx1 x2 ...xm

)2

(4.15)

 

å( yi − y)2

 

 

yx1 x2

...xm

 

 

При линейной зависимости признаков формула коэффициента множественной корреляции может быть представлена следующим выражением:

R

yx1x2

...x m

=

β×r

yxi

,

 

(4.16)

 

 

å i

 

 

 

где βi – стандартизованные коэффициенты регрессии;

ryx

i

– парные коэффициенты корреляции

 

 

 

 

 

 

 

 

результата с каждым фактором.

Формула коэффициента множественной корреляции для линейной регрессии получила название линейного коэффициента множественной корреляции, или, что то же самое, совокупного коэффициента корреляции.

Возможно также при линейной зависимости определение совокупного коэффициента корреляции через матрицу парных коэффициентов корреляции:

 

 

Ryx x

,...,x

 

=

 

1−

 

r

 

,

 

 

 

 

(4.17)

p

 

r11

 

 

 

 

 

 

 

1 2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

где

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

ryx

 

ryx

...

 

ryx

 

p

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

2

 

 

 

 

 

 

 

 

 

ryx

 

 

1

rx x

...

 

rx x

 

p

 

 

 

1

 

 

 

 

 

1 2

 

 

 

1

 

 

 

Dr =

 

ryx

 

 

rx x

 

1

...

 

rx x

 

p

(4.18)

 

 

2

 

 

2 1

 

 

 

 

 

 

2

 

 

 

 

 

...

 

 

...

 

...

...

 

...

 

 

 

 

 

 

ryxp

 

 

rxpx1

rxp x2

...

 

1

 

 

 

– определитель матрицы парных коэффициентов корреляции;

 

 

 

 

 

 

 

 

 

 

 

1

 

rx x

...

 

rx x

p

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1 2

 

 

 

1

 

 

 

r11=

 

rx x

 

1

 

... rx x

 

p

 

 

 

 

 

2 1

 

 

 

 

 

 

 

2

 

 

 

(4.19)

 

...

 

...

...

 

...

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

rx x

 

rx x

...

 

1

 

 

 

 

 

 

 

 

 

p 1

 

p

2

 

 

 

 

 

 

 

 

 

– определитель матрицы межфакторной корреляции.

Как видим, величина множественного коэффициента корреляции зависит не только от корреляции результата с каждым из факторов, но и от межфакторной корреляции. Рассмотренная

44

формула позволяет определять совокупный коэффициент корреляции, не обращаясь при этом к уравнению множественной регрессии, а используя лишь парные коэффициенты корреляции.

Скорректированный коэффициент множественной корреляции содержит поправку на число

2

степеней свободы, а именно остаточная сумма квадратов å(yi −yˆx1x2 ... xm ) делится на число

степеней свободы остаточной вариации (n −m) , а общая сумма квадратов отклонений å( yi − y)2

на число степеней свободы в целом по совокупности (n −1) .

Формула скорректированного коэффициента множественной детерминации имеет вид:

 

 

R2

= 1−

å( yi − yˆi )2 /(n − m)

,

(4.20)

 

 

 

 

 

 

 

ск

 

 

 

å( yi − y)2 /(n −1)

 

 

 

 

 

 

 

 

где m – число оцениваемых параметров уравнения регрессии; n – число наблюдений.

 

Поскольку

å( yi − yˆi )2

= 1− R

2

, то величину скорректированного индекса детерминации

å( yi − y)2

 

 

 

 

 

 

 

 

 

 

 

можно представить в виде:

 

 

 

 

 

 

 

 

 

 

 

Rск2

=1 - (1 - R2 ) ×

n −1

.

(4.21)

 

 

 

 

 

 

 

 

 

 

n - m

 

Чем больше величина m, тем сильнее различия Rск2 и R 2 .

Как было показано выше, ранжирование факторов, участвующих во множественной линейной регрессии, может быть проведено через стандартизованные коэффициенты регрессии ( β - коэффициенты). Эта же цель может быть достигнута с помощью частных коэффициентов корреляции (для линейных связей). Кроме того, частные показатели корреляции широко используются при решении проблемы отбора факторов: целесообразность включения того или иного фактора в модель можно доказать величиной показателя частной корреляции.

4.3.2. Частные и общий коэффициенты корреляции

Частные коэффициенты корреляции характеризуют тесноту линейной связи между результатом и соответствующим фактором при элиминировании (устранении влияния) других факторов, включенных в уравнение регрессии.

Показатели частной корреляции представляют собой отношение сокращения остаточной дисперсии за счет дополнительного включения в анализ нового фактора к остаточной дисперсии, имевшей место до введения его в модель.

В общем виде при наличии m факторов для уравнения

y = a + b x + b x

...+ b x + ε

(4.22)

1 1 2 2

m m

 

коэффициент частной корреляции, измеряющий влияние на y фактора xi , при неизменном уровне других факторов, можно определить по формуле:

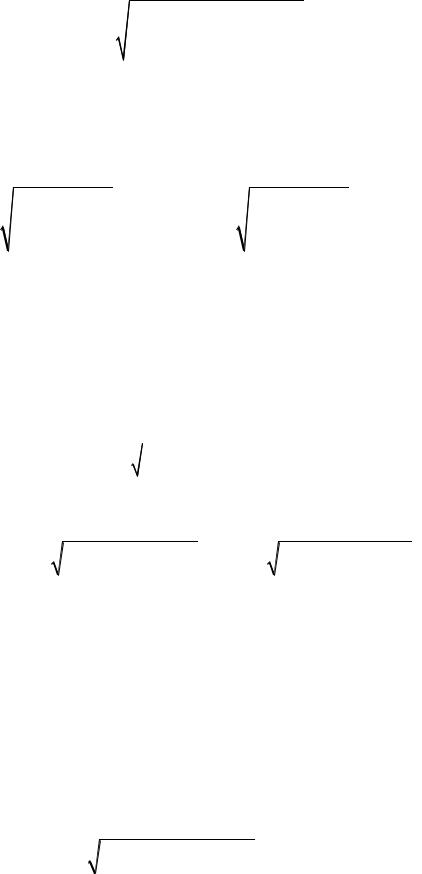
где

Ryx2

x

...x ...x

m

 

 

1 2

i

45

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ryx

 

 

 

=

1-

 

1- Ryx2

x

...x

...x

m

 

 

 

×x x

...x x

...x

 

1 2

 

i

 

 

,

(4.23)

2

 

 

 

 

 

 

i

1 2

i 1−i +1

m

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1- Ryx x

...x

x

i+1

...x

m

 

 

 

 

 

 

 

 

1 2

 

i1−

 

 

 

– множественный коэффициент детерминации всех m факторов с результатом;

R2

...x

x

 

...x

 

– тот же показатель детерминации, но без введения в модель фактора x .

yx x

i+1

m

 

 

 

 

 

 

 

 

 

 

 

 

 

 

i

1 2

 

i−1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

При двух факторах формула (4.23) примет вид:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ryx1×x2 =

1−

1− Ryx2

x

 

 

ryx2×x1 =

1−

1− Ryx2

x

 

 

 

 

 

1− r2

 

 

 

1− r2

 

 

 

 

 

 

 

 

 

 

 

 

 

1 2

;

 

 

 

1 2

.

(4.24)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

yx

2

 

 

 

 

 

yx

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

Порядок частного коэффициента корреляции определяется количеством факторов, влияние

которых исключается. Например, ryx1×x2 – коэффициент частной линейной корреляции первого

порядка. Соответственно коэффициенты парной линейной корреляции называются коэффициентами нулевого порядка. Коэффициенты частной корреляции более высоких порядков можно определить через коэффициенты частной корреляции более низких порядков по рекуррентной формуле:

ryxi ×x1x2 ...xi−1xi+1...xm

=

ryxi ×x1x2 ...xi−1xi+1...xm−1 - ryxm×x1x2...xm−1

× rxixm×x1x2...xi−1xi+1...xm−1

.(4.25)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1- r2

×x x ...x

 

× 1- r2

 

×x x

...x

x

...x

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

yx

m−1

 

 

x x

m

m−1

 

 

 

 

 

 

 

 

 

 

 

 

m

1 2

 

 

i

1 2

 

i−1

i+1

 

 

При двух факторах данная формула примет вид:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ryx1×x2

=

 

ryx

- ryx

2

× rx x

2

 

 

 

; ryx2×x1

=

 

ryx

- ryx

× rx x

2

 

 

 

 

 

 

1

 

 

1

 

 

 

 

2

 

 

1

 

1

 

 

.

 

(4.26)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1- r2

× 1- r2

 

 

1- r2

×

1- r2

 

 

 

 

 

 

yx

 

 

 

 

x x

 

 

 

 

 

 

 

yx

 

 

 

x x

 

 

 

 

 

2

 

 

 

 

1

2

 

 

 

 

 

 

 

 

1

 

 

 

1

2

 

 

 

 

Для уравнения регрессии с тремя факторами частные линейные коэффициенты корреляции второго порядка определяются на основе частных коэффициентов корреляции первого порядка. Так,

по уравнению y = a + b1x1 + b2x2 + b3x3 + ε возможно исчисление трех частных коэффициентов корреляции второго порядка:

ryx1×x2x3 , ryx2×x1x3 , ryx3×x1x2 ,

каждый из которых определяется по рекуррентной формуле. Например, при i =1 имеем формулу

для расчета ryx1×x2x3 :

ryx1×x2x3

=

 

ryx ×x

2

- ryx ×x

× rx x ×x

 

 

 

 

1

 

 

3

2

1

3

 

2

 

.

(4.27)

 

 

 

 

 

 

 

 

 

 

 

 

1− r2

 

 

1 − r

2

 

 

 

 

 

 

 

yx ×x

 

 

x x ×x

 

 

 

 

 

 

 

 

3

2

 

 

 

1

3

2

 

 

 

Рассчитанные по рекуррентной формуле частные коэффициенты линейной корреляции изменяются в пределах от –1 до +1, а по формулам через множественные коэффициенты детерминации – от 0 до 1. Сравнение их друг с другом позволяет ранжировать факторы по тесноте их

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
Помощь Обратная связь Вопросы и предложения Пользовательское соглашение Политика конфиденциальности