18
Рисунок 2.3. Наклон линии регрессии в зависимости от значения параметра b. Интервальная оценка параметра α на уровне значимости α имеет вид:
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
α − t1−α ;n−2 Sεi |
å(xi )2 |
|
|
≤ α ≤ α + t1−α ;n−2 Sεi |
|
|
å( xi )2 |
|
|
|
||||||||
|
|
|
|
i=1 |
|
|
|
|
i=1 |
. |
(2.25) |
|||||||||||
|
|
|
|
n |
|
|
|
|
|
n |
(xi − x)2 |
|||||||||||
|
|
|
|
|
|
nå |
( xi − x)2 |
|
|
|
|
|
|
|
nå |
|
|
|
||||
|
|
|
|
|
|
i=1 |
|
|
|
|
|
|
|
|
|
|
|
i=1 |
|
|
|
|
|
|
При построении доверительного интервала для параметра δ 2 |
исходят из того, что статистика |
|||||||||||||||||||
nS |
2 |
имеет |
2 |
-распределение с k = |
n – 2 степенями свободы. Поэтому интервальная оценка для |
|||||||||||||||||
δ 2 |
χ |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
δ 2 |
на уровне значимости α имеет вид: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
nS 2 |
|
nS 2 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
εi |
≤ δ 2 ≤ |
|
|
εi |
|
|
|
|
|
|
(2.26) |
|
|
|
|
|
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
χα |
;n−2 |
|
χ1−α |
;n−2 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Доверительный интервал выбирается таким образом, чтобы вероятность
æ |
χ |
2áχ |
|
|
|
|
ö |
= |
æ |
χ |
2 > |
χ |
|
|
|
|
|
ö |
= |
α |
. |
|
Pç |
2 |
|
|
|
÷ |
Pç |
2 |
|
|
|
|
÷ |
|
(2.27) |
||||||||
ç |
|
|
1−α |
;n |
− |
2 |
÷ |
|
ç |
|
|
|
1− |
α |
;n |
− |
2 |
÷ |
|
2 |
|
|
è |
|
|
2 |
|
ø |
|
è |
|
|
|
|
2 |
|
ø |
|
|
|
2.4. Оценка значимости уравнения регрессии (адекватности имеющимся статистическим данным)
2.4.1. Основная идея дисперсионного анализа
Для того чтобы проверить значимость уравнения регрессии необходимо установить, соответствует ли математическая модель, выражающая зависимость между переменными, экспериментальным данным и достаточно ли включенных в уравнение объясняющих переменных (одной или нескольких) для описания зависимой переменной.
19
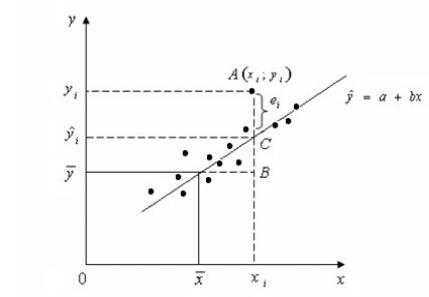
Рисунок 2.4
На рисунке 2.3 изображены наблюдаемые значения переменных xi , yi, соответствующая этим значениям линия регрессии, обозначены составляющие регрессии:
AB = yi − y; AC = yi − yˆ; CB = yˆi − y. |
|
По рисунку AB = CB + AC или yi − y = ( yi − yˆ) + ( yˆi − y), |
|
где yˆi = a +bxi – ордината точки прямой, соответствующей уравнении регрессии, |
имеющей |
абсциссу xi. |
|
Возведя обе части в квадрат и просуммировав выражение для каждого i-го случая, имеем
|
|
|
|
|
n |
2 |
n |
n |
n |
|
|
|
|
|
å( yi − y) |
|
= å( yˆi − y)2 + å( yi − yˆi )2 + |
2å( yi − yˆi )( yˆi − y) ≈ |
|
||
|
|
|
|
|
i=1 |
|
i=1 |
i=1 |
i=1 |
(2.28) |
|
|
|
|
|
|
|
n |
n |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
≈ å( yˆi − y) |
2 + å( yi − yˆi )2 , |
|
|
|
|
|
|
|
|
|
i=1 |
i=1 |
|
|
n |
− y) |
2 |
|
|
|
|
|
|
|
|
где Q = å( yi |
|
- полная сумма квадратов; |
|
|
|
|||||
i=1 |
|
|
|
|
|
|
|
|
|
|
n |
|
|
2 |
|
|
|
|
|
|
|
QR = å( yˆi − y) |
|
- сумма квадратов, объясненная моделью; |
|
|
||||||
i=1 |
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
2 |
n |
|
|
|
|
|
Q = å( yi − yˆi ) |
|
= åei2 - остаточная сумма квадратов. |
|
|
||||||
i=1 |
|
|
|
|
i=1 |
|
|
|
|
|
Если поделить выражение на n , то получим |
|
|
|
|||||||
|
|
|
|
|
|
|
var( y) =var( yˆ) +var( e) , |
|
(2.29) |
|
то есть дисперсия переменной у частично объясняется изменчивостью |
yˆ , а частично изменчивостью |
|||
остатка регрессии. |
|
|
|
|
Оценка этой изменчивости |
|
|
|
|
SR2 = |
QR |
|
(2.30) |
|
m −1 |
||||
|
|
|||
20
SR2 – обусловлена уравнением регрессии или объясняющей |
переменной, |
|||
S 2 |
= |
Qe |
|
(2.31) |
|
||||
εi |
|
n -m |
|
|
|
|
|
||
Sε2i – воздействием неучтенных случайных факторов и ошибок.
2.4.2. Процедура проверки значимости линейной связи между переменными
Эта процедура будет иметь смысл при соблюдении стандартных предположений о модели. Чтобы иметь общее суждение о качестве модели из относительных отклонений по каждому
наблюдению, определяют среднюю ошибку аппроксимации:
|
|
|
1 |
n |
yi - yˆi |
n |
ei |
|
|
|
|
|
= |
å |
×100% = å |
. |
(2.32) |
||||
A |
||||||||||
|
n |
yi |
||||||||
|
|
|
i=1 |
i=1 |
yi |
|
|
Средняя ошибка аппроксимации не должна превышать 8–10%.
Оценка значимости уравнения регрессии в целом производится на основе F -критерия Фишера, которому предшествует дисперсионный анализ. Согласно основной идее дисперсионного
анализа, общая сумма квадратов отклонений переменной y от среднего значения y раскладывается
на две части – «объясненную» ( SR2 ) и «необъясненную» ( Sε2i ).
Случайные величины |
SR2 = |
QR |
|
и |
Sε2i = |
Qe |
имеют χ2 -распределение |
|
m −1 |
n − m |
|||||||
|
|
|
|
|
||||
соответственно с (m-1) и (n-m) степенями свободы. Поэтому уравнение регрессии значимо на уровне α, если фактически наблюдаемое значение статистики
|
|
|
|
|
|
F = |
Q |
|
(n − m) |
= |
S 2 |
> F |
|
|
|
|
|
|
|
|
|
|
R |
|
R |
|
, |
(2.33) |
|||
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
Q (m −1) |
|
S 2 |
α ;k ;k |
|
||||
|
|
|
|
|
|
|
|
1 |
2 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
εi |
|
|
|
|
|
n |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
где QR |
= å( yˆi − y) |
|
- сумма квадратов, объясненная моделью; |
|
|
|
|||||||||
|
i=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
− yˆi ) |
2 |
n |
|
|
|
|
|
|
|
|
|
|
Q |
= å( yi |
|
|
= åei2 - остаточная сумма квадратов; |
|
|
|
||||||||
|
i=1 |
|
|
|
|
i=1 |
|
|
|
|
|
|
|
|
|
m – число оцениваемых параметров уравнения регрессии; |
|
|
|
||||||||||||
n |
– число наблюдений; |
|
|
|
|
|
|
|
|
|
|||||
Fα;k ;k |
2 |
– табличное значение критерия. |
|
|
|
|
|
|
|||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В случае линейной парной регрессии m=2 и уравнение регрессии значимо на уровне |
|||||||||||||||
значимости α, если |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
F = QR (n − 2) > F |
|
|
(2.34) |
||||||
|
|
|
|
|
|
|
|
|
Qe |
|
|
α:1:n−2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Одной из наиболее эффективных оценок значимости уравнения регрессии является коэффициент детерминации. Он характеризует степень выраженности связи между переменными. Определяется по формуле:
|
|
|
|
|
|
|
|
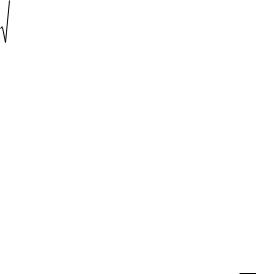
21 |
R |
2 |
|
QR |
|
Q |
|
||
|
= |
|
= |
1− |
|
. |
(2.35) |
|
|
Q |
Q |
||||||
Величина R2 показывает, какая доля вариации зависящей переменной |
обусловлена |
|||||||
вариацией объясняющей переменной. Так как 0 ≤ QR |
≤ Q , то 0 ≤ R2 ≤ 1 . |
|
||||||
Свойства коэффициента детерминации: |
|
|
|
|
||||
1.При R2 →1 регрессия хорошо отражает эмпирические данные, наблюдения примыкают к линии регрессии.
2.При R2 =1 точки (xi ; yi ) лежат на линии регрессии и между переменными существует линейная функциональная зависимость.
3.При R2 = 0 вариация зависимой переменной полностью обусловлена воздействием неучтенных в модели переменных и линия регрессии параллельна оси ОХ.
Если известен коэффициент детерминации R2, то критерий значимости уравнения регрессии
F = |
|
R 2 (n − m) |
> F |
(2.36) |
|
(1 |
− R 2 )(m −1) |
||||
|
α;k1 |
;k2 |
В случае линейной регрессионной модели коэффициент детерминации равен квадрату коэффициента корреляции.
R2 = r 2 xy |
(2.37) |
2.4.3. Оценка статистической значимости коэффициентов парной линейной регрессии и корреляции
В парной линейной регрессии оценивается значимость не только уравнения в целом, но и отдельных его параметров. С этой целью по каждому из параметров определяется его стандартная ошибка: Sb и Sa .
Стандартная ошибка коэффициента регрессии определяется по формуле:
|
|
|
|
|
|
Sb = |
|
Sεi |
|
|
|
|
|
|
|
|
|
|
|
, |
(2.38) |
||
|
|
|
|
|
|
å( xi − x)2 |
|||||
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
i=1 |
|
|
|
|
|
|
n |
|
n |
|
|
|
|
|
|
где |
S 2εi |
|
å( yi − yˆi )2 |
|
å ei2 |
– остаточная дисперсия. |
|
|
|
||
= |
i=1 |
= = |
i=1 |
|
|
|
|||||
|
|
|
|
|
|
|
|||||
|
n − m |
n − m |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
||
|
Величина стандартной ошибки совместно с t -распределением Стьюдента при |
( n − 2) |
|||||||||
степенях свободы применяется для проверки существенности коэффициента регрессии и для расчета его доверительного интервала.
Для оценки существенности коэффициента регрессии его величина сравнивается с его
стандартной ошибкой. Определяется фактическое значение t -критерия Стьюдента tb = b , которое
Sb
затем сравнивается с табличным значением при определенном уровне значимости α и числе