10
1.4.Типы данных при эконометрическом моделировании
1.4.1.Пространственные данные
Это данные в определенный момент времени. Например:
-набор сведений (объем производства, количество работников, доход и др,) по разным фирмам в один и тот же момент времени (пространственный срез);
-данные по курсам покупки/продажи наличной валюты в какой-то день по городу.
1.4.2.Временные ряды
Данные через определенные отрезки времени. Например:
-ежеквартальные данные по инфляции, средней заработной плате, национальному доходу, денежной эмиссии за последние годы;
-ежедневный курс доллара США, цены фьючерсных контрактов на поставку доллара США, котировки акций за ряд последних лет.
Отличительной чертой временных рядов является то, что они естественным образом упорядочены по времени, кроме того, наблюдения в близкие моменты времени часто бывают зависимыми.
1.5.Основные положения регрессионного анализа
В регрессионном анализе объясняемая переменная у представляется в виде функции
y = M y (x1 , x2 ,..., xn ) +ε , |
(1.15) |
где M y (x1 , x2 ,..., xn ) – функция, значение которой является условным |
математическим |
ожиданием величины у, полученным при данном наборе значений объясняющих переменных |
|
(функция регрессии); |
|
ε - случайная составляющая. |
|
В случае парной регрессии |
|
у = My (x) + ε. |
(1.16) |
Для линейной парной регрессии вид модели: |
|
yi =α + β xi +ε , |
(1.17) |
где (xi; yi)- элементы выборки, содержащей n пар значений переменных.
Стандартные предположения регрессионного анализа (предположения о процессе
порождения данных): |
|
|
|
|
1. |
В модели не все значения x1, х2, …, хn |
совпадают |
между собой |
(условие |
|
|
n |
2 |
|
идентифицируемости), тогда можно вычислить величину |
å(xi - x ) |
¹ 0 , входящую в формулы |
||
i=1
числовых характеристик величины х.
2. Значения y1, y2, ..., yn получаются наложением на значения (α + βxi) случайных ошибок εi, то есть значения (α + βxi) рассматриваются как некоторые постоянные, хотя и неизвестные наблюдателю. А значения y1, y2, ..., yn носят случайный характер, определяемый случайным
11
характером εi. Это условие предполагает отсутствие автокорреляционной зависимости остатков от номера наблюдения.
3. Ошибки ε1, ε2,..., εn – независимые случайные величины, имеющие нормальное распределение. Соответственно и y1, y2, ..., yn – независимые случайные величины. Математическое ожидание ошибок Mεi= 0.
Некоторые сведения из теории вероятностей.
Предположим, что задана функция распределения случайной величины ε i , то есть для
каждого - ∞ ≤ x ≤ ∞ определена вероятность F(x) того, что наблюдаемое значение отклонения ε i не превзойдет величину x, причем эта вероятность не зависит от номера наблюдения i =1, 2, …, n
|
|
F(x)=P(εi ≤ x). |
(1.18) |
|||
Тогда плотность распределения вероятностей ε i то есть закон распределения |
|
|||||
f(x)=F'(x). |
(1.19) |
|||||
Нормальным называют распределение вероятностей непрерывный случайной величины, |
||||||
которое описывается плотностью |
|
|
|
|
|
|
f (x) = |
|
1 |
|
e−( x−m)2 / 2δ 2 , |
(1.20) |
|
δ |
|
|
|
|||
2π |
||||||
где m - математическое ожидание,
δ- среднеквадратическое (стандартное) отклонение.
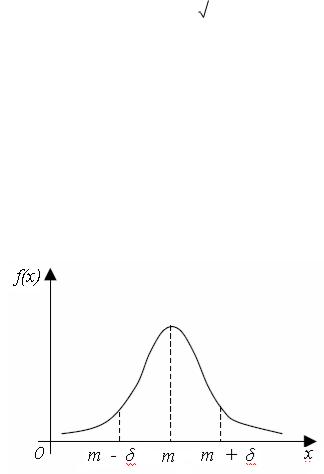
График плотности нормального распределения называют нормальной кривой (кривой Гаусса), он представлен на рисунке 1.8.
График симметричен прямой х = m, точки m - δ и m + δ являются точками перегиба. Площадь фигуры между графиком и осью ox равна 1.
Нормальное распределение часто приемлемо для описания случайных ошибок в моделях наблюдений, где результирующая ошибка является следствием сложения большого количества независимых случайных ошибок, каждая из которых достаточно мала.
Рисунок 1.8
4. Дисперсия ошибок εi (соответственно и величины y i ) постоянна для любого i. var(εi ) = δ 2 (εi ) = const , var( yi ) = δ 2 ( yi ) = const . (1.21)