§3. Oтсроченные m-кратные ренты и непрерывные ренты

3.1. Отсроченные ренты

Рассмотрим обобщение базовых рент, когда первая из последовательности n единичных выплат происходит в момент

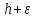
для пренумерандо и 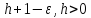– для постнумерандо (рис.1.2).

Рис. 1.2

Определение. Такой поток платежей называется отсроченной на h единиц времени рентой (deferred annuities), а его современную стоимость в момент 0 обозначают через 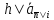для выплат пренумерандо через 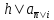- для выплат пренумерандо, n=1,2,…, 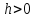. Приh=0 отсроченная рента совпадает с базовой.

Поскольку

,

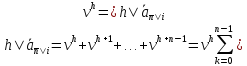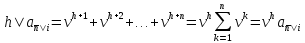(1.22)

То для вычисления современной стоимости ренты можно использовать (1.6) при любых значениях , включая дробные. Вместе с тем при любом целомh=1,2, и n=1,2,

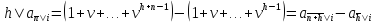
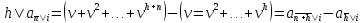(1.23)

Таким образом, при 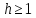для вычисления коэффициентов дисконтирования отсроченной ренты можно пользоваться как (1.22), так и (1.23), а при любом, включая дробные, только (1.22)

Как и следовало ожидать из финансовых соображений, коэффициенты дисконтирования (1.22)-(1.23) отсроченной ренты при h=0 совпадают с 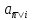и

3.2. M-кратные ренты

Как это часто бывает на практике, выберем теперь за базовую единицу времени 1 год. Обозначим эффективную ставку через i и примем, что за год производится m равностоящих выплат по 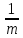ден. ед. каждая, причем проценты начисляются также m раз, m=1,2… . Общее число выплат за интервал времени в n лет составит nm, а общая сумма выплат при i=0 составит n ден. ед. Для ренты постнумерандо выплаты производятся и проценты начисляются в моменты

m выплат m выплат

…, ,

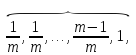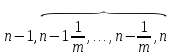а для выплат пренумерандо – в моменты

m выплат m выплат

, .

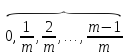Заметим, что предпоследняя операция постнумерандо и последняя операция пренумерандо производится в момент

.

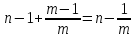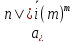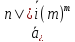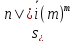Обозначим коэффициенты дисконтирования рент постнумерандо и пренумерандо в случае m выплат и m начислений соответственно и, а коэффициенты наращения – соответственнои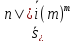. Для краткости в промежуточных результатах мы будем иногда опускать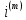в нижнем индексе.

Приводя стоимость всех выплат ренты постнумерандо к моменту 0, получим:

.

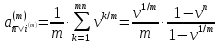Так как 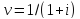, то

.

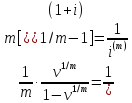Здесь мы воспользовались формулой (6,4), связывающей номинальную ставку 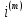с эффективной годовой ставкойi.

Следовательно,

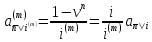(1.24)

Аналогичным образом,

.

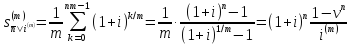Поэтому, как и следовало ожидать из финансовых соображений,

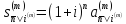(1.25)

Проводя аналогичные алгебраические выкладки для ренты пренумерандо, получим.

, (1.26)

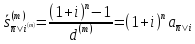. (1.27)

Таким образом, мы обобщили случай однократных рент на случай (l,m)-кратных в том наиболее частом случае, когда число l выплат за год совпадает с количеством m начислений за год.

Заметим, что рента с m-кратным начислением процентов, m выплатами по 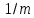ден. ед. за год, номинальной годовой ставкойи срокомn лет эквивалентна однократной ренте с периодом 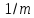лет, выплатой по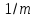ден. ед., процентной ставкой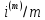за период и срокомnm периодов.

,

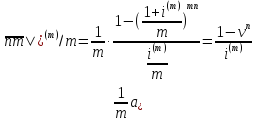То

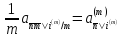. (1.28)

3.3 Непрерывные ренты

Пусть на интервале от начального момента 0 до конечного момента 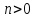рента выплачивается очень часто, так что ее можно считать непрерывной. Очевидно, что при непрерывной выплате различие между рентами пренумерандо и постнумерандо исчезает. Современную стоимость ренты, выплачиваемой непрерывно с постоянной интенсивностью одна денежная единица за одну единицу времени при непрерывном начислении процентов с постоянной интенсивностью δ обозначим. 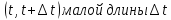Так как за интервалбудет выплачена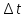ден. ед., а приведенная на момент 0 стоимость этой суммы составит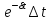, то после суммирования по интервалу (0,n) и перехода к пределу по 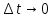получим:

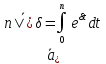. (1.29)

Здесь n – любое неотрицательное число, не обязательно целое. Если δ = 0, то 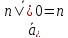, что следует из финансовых соображений. Поскольку при непрерывном начислении процентов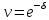, то при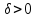из (1.29) следует, что

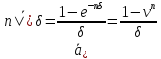(1.30)

Или

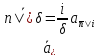. (1.31)

Пусть h –любое неотрицательное число, не обязательно целое, а 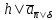- современная стоимость отсроченной наh единиц времени ренты, выплачиваемой непрерывно с интенсивностью 1 на интервале (h,h+n). Тогда

.

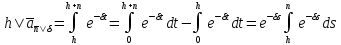Следовательно, отсроченную непрерывную ренту легко выразить через немедленную:

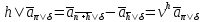. (1.32)

Повторяя рассуждения, сделанные при выводе формулы (1.32) для коэффициентов наращения 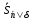непрерывной немедленной ренты, получим:

.

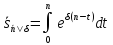Отсюда следует, что

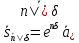(1.33)

Или

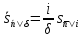(1.34)

Формула (3.14) сразу следует из финансовых соображений, так как

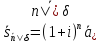
Теорема 1.1. Для бессрочной ренты

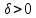
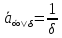
Доказательство следует из (1.30), так как

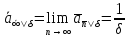
Из (2.6) и (3.10) следует

Теорема 1.2 . Для любых n=1,2, и любых m=1,2 имеет место:

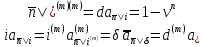(1.35)

Теорема 1.3. Для любых n=1,2 и любых m=1,2 имеет место:

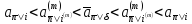(1.36)

Это неравенство позволяет банку правильно рассчитать себестоимость ренты, а клиенту при фиксированной цене ренты, фиксированном сроке n и фиксированной эффективной ставке i выбрать наиболее выгодную для него схему выплат. Очевидно, что при прочих равных условиях наиболее выгодной является выплата пренумерандо в начале каждого периода ренты.