PraktykumD+ICh

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный технический университет Украины «Киевский политехнический институт»

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

x 1 0 ln(1

.pdf

Скачиваний:

Добавлен:

12.05.2015

Размер:

3.41 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 1213 / 1813 14 15 16 17 18 > Следующая >>>

9. Правило Бернуллі — Лопіталя

121

lim	(x	2		lim	2x
			)
x	(e	x		x	e	x
			)
					2
lim	(2x)			lim

x (ex )				x ex

0 M L.

x50 2x 1

3) lim

x 1

100

2x 1

50x

lim

2x 1)

lim

x 1

100

x 1

2x 1)

100x

x sin x

lim

2x sin x

lim

(x sin x)

lim

1 cos x

(2x sin x)

2 cos x

тобто правило Бернуллі — Лопіталя не застосовне, але

x sin x

sin x

1 .

lim

2x sin x

sin x

5) lim (1 x)ln x [00 ]

ln x (x 1),

lim

ln(1 x ) (x 1)

ex 1 0

x 1 0

ln(1 x)

lim

exp

x 1 0

lim

(1 x)

exp lim

1 L.

x 1 0

Коментар. Щоб перетворити вираз на частку при потребі використовують формули:

fg	f	g	; f g eg ln f (f 0);	f g	g1	1f	.
fg	g 1	f 1	; f g eg ln f (f 0);	f g	1	1	.
	g 1	f 1			1	1
					f	g

Задачі для аудиторної і домашньої роботи

9.7.Нехай f (x) x(x 1)(x 2)(x 3). Доведіть, що всі три корені рів-

няння f (x) 0 дійсні.

9.8.Доведіть, що рівняння 16x4 64x 31 0 не може мати двох різних дійсних коренів у інтервалі (0;1).

122 Розділ 2. ДИФЕРЕНЦІАЛЬНЕ ЧИСЛЕННЯ ФУНКЦІЙ ОДНІЄЇ ЗМІННОЇ

9.9.Доведіть, що рівняння ex 1 x 2 0, яке має корінь x 1 (перевірте!), не має інших дійсних коренів.

9.10.Застосовуючи Лаґранжову формулу для функції f(x) 3x3 3x на відрізку [0;1], визначте точку x , що фігурує у формулі.

9.11. Застосовуючи

Лаґранжову

формулу,

доведіть

нерівність

ex 1 x, x 0.

9.12. Застосовуючи		формулу Коші для функцій f (x) 2x 3 5x 1 та
g(x) x2	4	на відрізку [0; 2], визначте точку x , що фігурує у фо-
рмулі.

9.13.Користуючись правилом Бернуллі — Лопіталя, знайдіть:

1)lim x100 x 2 ;

x 1 x50 x 2

3)lim ln sin ax ;

x0 ln sin bx

5)lim x sin x ;

x0 x tg x

9)lim (xne x );

11)	lim sin(x 1) tg				x	;
	x 1				2
			1
13)	lim		1
13)	lim	ctg x		;

	x 0

15)lim (( 2 arctg x) ln x);

17)lim (arcsin x)tg x ;

19)lim (ctg x)1 ln x ;

2)lim 2x 3x ;

x0 4x 5x

4)lim 3x 35 ;

x5 x 5

6) lim ln x	;
x x 3

8)lim e x cos x ;

x0 e x cos x

		x	1
10) lim				;
10) lim				;
x 1
	x 1		ln x

12)lim (x ln3 x);

14) lim ln x ln(x 1);

x1 0

16)lim xsin x ;

18) lim x1 x ;

20) lim (tg x)2x .

x 2 0

												10. Тейлорова формула																	123
9.14.	Перевірте, що						lim					x sin x						існує, але його не можна обчислити за пра-
							x x sin x
	вилом Бернуллі — Лопіталя.
Відповіді
9.10.			1		. 9.12.			1		,	2		5	.
9.10.					. 9.12.					,				.
	3				1		2					3
	3						2					3
9.13. 1)		101		;	2)	ln 2 ln 3			; 3)			1; 4)				2	; 5)		1	; 6)	0; 7)	;	8)	; 9)	0;	10)	1	;	11)	2	;
9.13. 1)				;	2)				; 3)			1; 4)					; 5)			; 6)	0; 7)	;	8)	; 9)	0;	10)		;	11)		;
	51					ln 4 ln 5									3	6 5			2								2

12); 13) 0; 14) 0; 15) 0; 16) 1; 17) 1; 18) 1; 19) e1 ; 20) 1.

10.Тейлорова формула

Навчальні задачі

10.1.Записати формулу Тейлора для нескінченно диференційовної функції f (x) у точці x0 :

1)2-го порядку із залишковим членом у формі Пеано;

2)3-го порядку із залишковим членом у формі Лаґранжа.

Розв’язання. [2.6.5, 2.6.6.]

f (x0)

(x0)

f (x) f (x0)

x0)

(x x0)

o((x x0) ), x x0.

1 !

2 !

f (x) f(x0)

f (x0)

x0)

1 !

f (x

f (x0 )

f (4)( )

x0 )

(x x

0 )

(x x

0 ) ,

(x0; x).

2 !

3 !

4 !

10.2.Функцію f (x) розвинути за степенями (x 2), якщо:

1)f (x) 2x4 5x3 3x2 8x 4;

2) f (x)	x	до члена, що містить (x				2)3.
2) f (x)	1 x	до члена, що містить (x				2)3.
Розв’язання. [2.6.5.]
1) Многочлен має похідні будь-якого порядку:
					f (2) 0;
	f (x) 8x3		15x2 6x 8,				f (2) 0;
	f			2	30x 6,
	f	(x) 24x			30x 6,	f (2) 30;
							66;
		f (x) 48x 30, f (2)					66;

124 Розділ 2. ДИФЕРЕНЦІАЛЬНЕ ЧИСЛЕННЯ ФУНКЦІЙ ОДНІЄЇ ЗМІННОЇ

f (4)(x) 48;

f (k)(2) 0, k

5, 6, ....

f (x) 15(x 2)2 11(x 2)3

2(x 2)4.

2) f (x)

, x0

2, n 3.

f (k)(2)

(x 2)k o (x 2)3 .

f(x)

k 0

k !

(x 1)4 .

f (x) (x 1)2

; f

(x) (x 1)3 ;

f (x)

f(2) 2,

f (2) 1;

(2)

f (2) 6.

f (x) 2 (x 2) (x 2)2 (x 2)3 o (x 2)3 .

10.3. Розвинути за степенями x

функцію f (x) ex ln(x 1) до члена, який

містить x 3 включно.

Розв’язання. [2.7.5, 2.7.6.]

[Записуємо формули Тейлора — Маклорена 3-го порядку для функцій f (x) ex

та f(x) ln(x 1).]

				ex		1 x						x		2			x 3			o(x 3 ),
				ex		1 x						2 !					3 !			o(x 3 ),
												2 !					3 !
				ln(1 x) x										x2				x3					o(x3).
				ln(1 x) x																			o(x3).
x							x	2		x	3			2				3	3						x	2			x	3			3
x							x			x								3							x				x				3
e ln(1 x) 1 x													o(x									x									o(x
e ln(1 x) 1 x													o(x						)			x									o(x			)
							2 !			3 !															2				3
							2 !			3 !															2				3

	2		1		3		1		1												3						x	2			x	3			3
x x	2	1	1	x	3		1		1				1			o(x					3		) x				x				x		o(x		3	).
x x		1		x												o(x							) x										o(x			).
							2		2																		2				3
			2				2		2				3														2				3
			ex ln(1 x) x												x2					x		3		o(x 3 ).
			ex ln(1 x) x													2					3			o(x 3 ).
																2					3

10.4. Обчислити 330 з точністю до 10 4 за допомогою Тейлорової формули.

Розв’язання. [2.7.3, 2.7.9.]

[Перетворюємо підкореневий вираз — шукаємо найближчий повний куб.]

								1				1

3	30	3	27	3	3	27	1		3	3	1		.
	30		27	3		27	1		3		1		.
												9
								9				9

10. Тейлорова формула

125

[Записуємо Тейлорову формулу для функції f (x) (1 x)1 3 і залишковий член у Лаґранжовій формі.]

	1 3			n		1	1				1					k
																k
		1										k		1	x		R (x),
(1 x)		1						1	...			k		1			R (x),
						3	3				3							n
						3	3				3				k !
			k 1
								n множників						n 1
		( 1)n 1			2 5 8...(3n 1)								1	n 1					1
R	(x)														,
																		0;		.
												2						0;		.
n										n		2
		(n 1)!				3n 1 1				n
		(n 1)!				3n 1 1						3	9						9

[Підбираємо такий порядок формули Тейлора, щоб залишковий член за модулем не перевищував заданої похибки.]

						2					5		1	2				1				4
						2				3			1					1				4
	3R1(x)						1														10		;
	3R1(x)						1														10		;
					3 2 !													5
					3 2 !								9		3		3
					2 5						8			1				5				4
					2 5						8			1				5
								1				3
	3R2(x)																			10				;
	3R2(x)																			10				;
					2													3	9
					3	3 !							9					3
		2 5 8							11		1	4			10					4
3R3(x)		2 5 8				1			3		1				10					4		n 3.
3R3(x)						1													10			n 3.
		3	3	4 !												12
		3		4 !							9				3

[Обчислюємо шукане значення за формулою Тейлора 3-го порядку, беручи в проміжних обчисленнях один запасний десятковий знак після коми.]

										2			3
3					1 1 1 2 1				1		1 2 5 1	1
3					1 1 1 2 1				1		1 2 5 1	1
	30	3	1
	30	3	1

					3 9 3 3 2 ! 9						3 3 3 3 !	9

3(1 0, 03703 0, 00137 0, 00008) 3 1, 03574 3, 10722.
						3		3, 1072 10 4.
						3	30	3, 1072 10 4.
10.5. Обчислити e0,1				з точністю до 0, 001.
Розв’язання. [2.7.3, 2.7.5.]

[Записуємо формулу Тейлора — Маклорена для ex із залишкови членом у Лаґранжовій формі.]

...

R (x),

1 !

n !

R (x)

xn 1, 0

[Визначаємо потрібний порядок Тейлорової формули, оцінюючи модуль залишкового члена.]

R (x)	e (0, 1)n 1	2	0, 001.


n	(n 1) !	10n 1(n 1)!

для зручності підсилюємо нерівність

126 Розділ 2. ДИФЕРЕНЦІАЛЬНЕ ЧИСЛЕННЯ ФУНКЦІЙ ОДНІЄЇ ЗМІННОЇ

										n 1 :				1		0, 001;
										n 1 :				100		0, 001;
														100
								n 2 :						1				0, 001.
								n 2 :					3000					0, 001.
													3000
	e0,1		1		0, 1			0, 01			1, 0000 0, 1000 0, 0050 1, 105.
						1 !		2 !
										e0,1 1, 105							10 3.
10.6.	Оцінити похибку, яку допускають,																обчислюючи значення ln 1, 5 за фор-
	мулою: ln(1 x) x x2											x 3			x 4 .
											2			3			4
Розв’язання. [2.7.3.] 
n 4.
						R4(x)					4 ! x5				, 0 x 0, 5.
						R4(x)						)4			, 0 x 0, 5.
									5 !(1			)4
			0 R			(x) max						1	(0, 5)5					(0, 5)5		0, 01 .
			0 R			(x) max												(0, 5)5		0, 01 .
				4				0 0,5				5 (1 )4							5
								0 0,5				5 (1 )4							5
			ln 1, 5 0, 5						1 (0, 5)2				1 (0, 5)3 1 (0, 5)4								0, 40.
									2					3					4
									ln 1, 5 0, 40 0, 01.
10.7.	Знайти lim x sin x , використовуючи формул Тейлора.
			x 0				x 3
Розв’язання. [2.7.7.]
		x sin x								x		x x3 o(x4 )								1		o(x		4		1
		x sin x											3 !							1		o(x			)	1
	lim						lim												lim							.


	x 0			3				x 0						3					x 0	3 !			3			6
			x									x								3 !		x				6
			x									x										x

Задачі для аудиторної і домашньої роботи

10.8.Розвиньте многочлен f (x) x4 5x3 x2 3x 4 за степенями двочлена x 4.

10.9. Розвиньте многочлен f (x) x3 3x2 2x 4 за степенями двочлена

x1.

10.10.Функцію f (x) (x2 3x 1)3 розвиньте за степенями x, застосовуючи Тейлорову формулу.

	10. Тейлорова формула		127
10.11.	Напишіть Тейлорову формулу 3-го порядку для функції y	x	при

		x 1
	x0 2 і побудуйте графіки заданої функції та її многочлена Тейлора 3-
	го степеня.
10.12. Напишіть Тейлорову формулу 3-го порядку для функції y tg x			при

x0 0 і побудуйте графіки заданої функції та її многочлена Тейлора 3-

го степеня.

10.13.Напишіть формулу Тейлора — Маклорена n -го порядку для функції y xex при x0 0.

10.14. Напишіть Тейлорову формулу n -го порядку для функції y 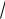x при x0 4.

10.15.Знайдіть перші три члени розвинення функції f (x) x10 3x6 x2 2

за Тейлоровою формулою при x0 1. Обчисліть наближено f (1, 03).

10.16.Знайдіть перші три члени розвинення функції

f (x) x 8 2x7 5x6 x 3

за Тейлоровою формулою при x0 2.	Обчисліть наближено			f(2, 02) та
(1, 97).
10.17. Застосовуючи наближену формулу ex	1 x	x2	, знайдіть	1		й оці-
10.17. Застосовуючи наближену формулу ex	1 x		, знайдіть			й оці-
		2			4 e

ніть похибку.

10.18. Обчисліть з абсолютною похибкою, меншою 0, 001, наближене значення:

1)	sin 1;				2)		e;
3)					4)	5
3)	ln 1, 05;				4)	5	33.
10.19. Знайдіть:
1)		cos x e x2		2	2)	lim		ex	sin x x(1 x)	.
	lim			;
	lim		x4	;					x 3
	x 0		x4			x 0			x 3

Відповіді

10.8.(x 4)4 11(x 4)3 37(x 4)2 21(x 4) 56;

10.9.(x 1)3 5(x 1) 8.

10.10.x6 9x5 30x4 45x3 30x2 9x 1.

128 Розділ 2. ДИФЕРЕНЦІАЛЬНЕ ЧИСЛЕННЯ ФУНКЦІЙ ОДНІЄЇ ЗМІННОЇ

10.11. 2 (x 2) (x 2)2 (x 2)3

(x 2)4

, 0 1.

2))

10.12. tg x x

x3 R (x).

10.13. x 1!

2 ! ...

Rn(x).

(n 1)!

10.14. 2 x 4

(x 4)2

(x 4)3

...

( 1)n 1

(2n 2)!

(x 4)n R (x).

512

!(n 1)! 24n 2

10.15.1 6(x 1) (x 1)2 ..., f(1, 03) 0, 82.

10.16.f(x) 321 1087(x 2) 1648(x 2)2 ..., f(2, 02) 343, 4, f(1, 97) 289, 9.

10.17.0, 78, 0, 01.

10.18. 1) 0, 842; 2) 1, 648; 3) 0, 049; 4) 2, 012.

10.19.1) 12 ; 2) 3 .

11. Дослідження функцій за допомогою похідних

Навчальні задачі

11.1. Знайти інтервали монотонності функції:

1) f (x) 4x 3 21x2 18x 7;					2) f(x) 8x2 x4 ;
		1
		1
			, x e,
			, x e,
3)		e
3)	f (x)	e
	ln x
				, x e.
				, x e.
		x
		x

Розв’язання. [2.9.1, 2.9.2, 2.910.]

1) [Крок 1. Визначаємо область означення.]

D(f ) ( ; ).

[Крок 2. Знаходимо критичні точки 1-го порядку: точки, в яких перша похідна функції рівна нулеві, або не існує.]

	2			1
f (x) 12x	2	42x 18 12(x 3)		1
f (x) 12x		42x 18 12(x 3)	x		.
				2
				2

f (x) 0 x1 12 , x2 3.

x ( ; ) f (x), f (x) .

Критичні точки: x1 21 , x2 3.

[Крок 3. Крок визначаємо знак похідної на кожному інтервалі монотонності.]

11. Дослідження функцій за допомогою похідних			129
знак f
поведінка f 21	3	x

[Крок 4. Застосовуємо достатні умови монотонності.] f : ( ; 12) (3; ); f : (21 ; 3).

2) D(f ) [ 8; 8].

16x 4x3

4 x2

f (x)

2 8x2 x4

8 x2

f (x) 0 : x

2, x

8 D;

(x) : x3,4

(x) : x

Критичними точками є x1

2, x2

0, x3

f 8 2 0 2 8 x

f : ( 8; 2) (0; 2); f : ( 2; 0) (2; 8). 3) D(f ) ( ; ).

Для x e f (x) 0.

Знайдемо ліву й праву похідні в точці x e :

f (e)

lim

f (e h) f (e)

h 0

f (e h) f (e)

ln(e h) 1

e ln(e h) e h

e h

f (e) lim

lim

h(e h)e

h 0

e ln(e h) e h

lim

h 0

e h

скористалися правилом Бернуллі -- Лопіталя

Отже, f (e) 0.

Для x e		1 ln x
	f (x)	x2
Отже,

.
		0,
		0,

	1	ln x
f (x)	1	ln x
				,
			2	,
		x	2
		x
x e f		(x) 0.

xe,

xe.

f const : ( ;e); f : (e; ).

130 Розділ 2. ДИФЕРЕНЦІАЛЬНЕ ЧИСЛЕННЯ ФУНКЦІЙ ОДНІЄЇ ЗМІННОЇ

11.2. Знайти екстремуми функції:

1)	y x 4	8x 2 12;	2) y x 3 x 1 2 ;
3)	y x2	ln x.
	2

Розв’язання. [2.9.4, 2.9.5, 2.9.10.]

1)D(y) ( ; ).

x ( ; ) y 4x 3 16x.

y 0 : x1 2, x2 0, x3 2. y , y x .

Критичні точки x1 2, x2	0, x3 2.
f
f	2	0	2	x
	min	max	min
ymin ( 2) ymin (2) 8, ymax (0)				12.

2) D(y) ( ; ).

												2x					5x 3
				3			2					2x					5x 3


y					(x		1) 33					x 1			33				x 1		.
																		3
		y			0 : 5x 3 0									x 5 .
		y			0 : 5x 3 0									x 5 .
		y : 3							x 1		0 x 1.
Критичні точки x1	3	, x2			1.
	5				f
					f
					f			3					1				x
					f		5						1				x
							5					min
							max					min

													3			3 3		4
													3			3 3		4		.
			ymin(1) 0, ymax																	.
																5		9
												5				5		9
3) D(y) (0; ).
														1		x2 1
	x D(f ) y									x x							x .
	x D(f ) y									x x							x .
Критична точка x 1.					y 0 : x1 1, x2 1.
Критична точка x 1.						f
						f
					f		0			1				x
										min

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 1213 / 1813 14 15 16 17 18 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
04.09.2019414.35 Кб1Poyasnyuvalna_zapiska (1).docx
#
04.09.2019986.31 Кб3Poyasnyuvalna_zapiska.docx
#
17.03.2016931.53 Кб4Poyasnyuvalna_zapiska_moya.docx
#
10.11.2018687.1 Кб6praktichni_roboti_po_visual_basic.doc
#
12.05.20153.46 Mб60Praktikum2_TBиМС.doc
#
12.05.20153.41 Mб13PraktykumD+ICh.pdf
#
12.05.20154.04 Mб26PraktykumLA+AG.pdf
#
12.05.20153.98 Mб47PraktykumLAAG.pdf
#
17.03.20163.49 Mб20PraktykumRiady.pdf
#
19.11.2018693.25 Кб9Prakt_BZhD_2011_2012.doc
#
23.11.2019120.32 Кб1prakt_rab_po_tekhnologiam.doc