
- •Федеральное агентство по образованию РФ
- •АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ
- •ТЕОРЕТИЧЕСКИЕ ОСНОВЫ АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ НА ПЛОСКОСТИ
- •1.ПРОСТЕЙШИЕ ЗАДАЧИ НА ПЛОСКОСТИ
- •1.1. Расстояние между двумя точками
- •1.2. Деление отрезка в данном отношении
- •1.3. Площадь треугольника
- •2. ПРЯМАЯ ЛИНИЯ НА ПЛОСКОСТИ
- •2.1. Общее уравнение прямой
- •2.2. Каноническое уравнение прямой
- •2.3. Уравнение прямой, проходящей через две точки
- •2.5. Уравнение прямой в отрезках
- •2.6. Нормальное уравнение прямой
- •2.7. Расстояние от точки до прямой
- •2.8. Координаты точки пересечения двух прямых
- •2.9. Угол между двумя прямыми
- •2.11. Уравнение пучка прямых
- •3. КРИВЫЕ ВТОРОГО ПОРЯДКА
- •3.1. Эллипс
- •3.2. Окружность
- •3.3. Гипербола
- •3.4. Парабола
- •4. ПРЕОБРАЗОВАНИЯ КООРДИНАТ
- •4.1. Параллельный перенос
- •4.2. Поворот координатных осей
- •4.3. Изменение начала координат и поворот осей
- •5. ЛИНИИ В ПОЛЯРНОЙ СИСТЕМЕ КООРДИНАТ
- •5.1. Полярные координаты на плоскости
- •5.2. Связь полярных координат с декартовыми
- •5.3.1. Кривые второго порядка
- •5.3.2. Спирали
- •5.3.3. Розы
- •6. ПАРАМЕТРИЧЕСКОЕ ЗАДАНИЕ ЛИНИЙ
- •6.1. Окружность
- •6.2. Циклоида
- •6.3. Астроида
- •7. КРИВЫЕ ТРЕТЬЕГО ПОРЯДКА
- •7.1. Полукубическая парабола
- •7.2. Локон Аньези
- •7.3. Декартов лист
- •8. КРИВЫЕ ЧЕТВЕРТОГО ПОРЯДКА
- •8.1. Улитка Паскаля
- •8.2. Кардиоида
- •8.3. Лемниската Бернулли
- •Парабола
- •РЕШЕНИЕ ЗАДАЧ ПО АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ НА ПЛОСКОСТИ
- •ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ
- •Вариант 1
- •ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА
- •1. Поверхности
- •1.1. Линейчатые поверхности
- •1.2. Поверхности вращения
- •1.3. Поверхности второго порядка
- •2.1. Эллипсоид
- •2.2. Гиперболоиды
- •2.2.1. Однополостный гиперболоид
- •2.2.2. Двуполостный гиперболоид
- •2.3. Параболоиды
- •2.3.1. Эллиптический параболоид
- •2.4. Конус
- •2.5. Цилиндры
- •2.5.1. Эллиптический цилиндр
- •2.5.2. Гиперболический цилиндр
- •2.5.3. Параболический цилиндр
- •РЕШЕНИЕ ТИПИЧНЫХ ЗАДАЧ
- •ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ
- •БИБЛИОГРАФИЧЕСКИЙ СПИСОК
Но λ не принимает значение -1, так как при λ =-1:
M1M = −MM 2 и M1M + MM 2 = M1M 2 = 0,
т.е. точка М1 совпадает с точкой М2, а мы предполагали их различными.
|
|
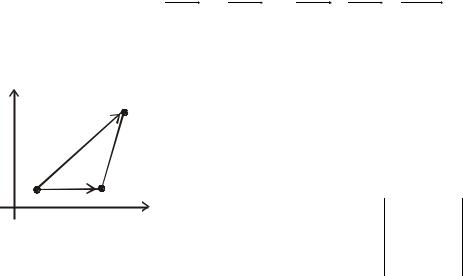
1.3. Площадь треугольника |
|||||
y |
M3 |
Пусть треугольник задан координатами своих вершин: |
|||||
|
|
|
М1(x1,y1), |
|
|||
|
|
|
M2(x2,y2), |
|
|||
|
|
Тогда |
M3(x3,y3). |
|
|||
M1 |
M2 |
|
x1 |
y1 |
1 |
||
|
|
||||||
0 |
|
x |
1 |
||||
|
|
S = |
x |
y |
|
1 |
|
|
|
|
2 |
2 |
|
2 |
1 |
|
|
|
|
x |
y |
||
|
|
|
|
3 |
|
3 |
|
При вычислении по этой формуле площадь получается положительной, если обход вершин в порядке нумерации происходит против часовой стрелки, и отрицательной – в противоположном случае.
Формула площади треугольника может быть записана в виде
S = |
1 |
|
|
|
x2 − x1 |
y2 |
− y1 |
|
|
|
. |
|
|
|
|
|
|||||||||
2 |
|
|
|
x |
− x |
y |
− y |
|
|
|
||
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
3 |
1 |
3 |
1 |
|
|
|
|
2. ПРЯМАЯ ЛИНИЯ НА ПЛОСКОСТИ
2.1. Общее уравнение прямой
Общее уравнение прямой на плоскости xoy получается из общего уравнения плоскости в пространстве при z=0.
Прямая на плоскости в декартовых координатах задается уравнением
Ax+By+C=0.
Если А=0 (В=0), то прямая параллельна оси ox (оси oy). Если С=0, то прямая проходит через начало координат.
Если прямая проходит через точку (x0,y0) перпендикулярно вектору n = {A, B}, ее уравнение принимает вид: A(x − x0 ) + B( y − y0 ) = 0 .
2.2. Каноническое уравнение прямой
Если прямая проходит через точку (x0,y0) параллельно направляющему вектору a ={l,m}, то из канонических и параметрических уравнений прямой в
пространстве при z=0 получаем каноническое и параметрические уравнения прямой на плоскости в виде:
x − x |
0 |
|
y − y |
0 |
x = x0 + lt, |
|
|
= |
|
и |
+ mt, |
||
l |
|
m |
|
|||
|
|
|
y = y0 |
|||
где t - параметр, t (−∞,∞) .
7

|
|
|
2.3. Уравнение прямой, проходящей через две точки |
|
|||||||||||||
Y |
|
|
|
Пусть на |
плоскости заданы |
две |
точки M1(x1,y1), |
||||||||||
|
|
|
M2 |
|
M2(x2,y2). Для того чтобы написать уравнение прямой, |
||||||||||||
|
|
|
|
|
проходящей |
|
через |
|
эти точки, |
полагаем |
в |
||||||
|
|
|
M1 |
|
соответствующем уравнении прямой в пространстве |
||||||||||||
|
|
|
|
|
X z = z1 = z2 = 0. |
Тогда |
|
получаем |
искомое уравнение |
в |
|||||||
O |
|
|
|
||||||||||||||
|
|||||||||||||||||
|
|
|
|
|
виде |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x − x1 |
|
= |
y − y1 |
. |
|
|
|
||||
|
|
|
|
|
|
x − x |
|
|
|
|
|||||||
|
|
|
|
|
|
|
y |
2 |
− y |
|
|
|
|||||
|
|
|
|
2 |
1 |
|
|
|
|
1 |
|
|
|
|
|||
2.4. Уравнение прямой, проходящей через данную точку в заданном направлении
Пусть прямая составляет угол α с осью ох. Угловым коэффициентом прямой k называется число k =tgα.
Прямая может быть задана точкой М1(x1,y1) и угловым коэффициентом k или двумя точками М1(x1,y1) и М2(x2,y2).
|
Уравнение прямой с угловым коэффициентом k может |
|||||
быть получено из общего уравнения прямой |
Ax+By+C=0, |
|||||
если |
B ≠ 0, тогда y = k x +b, где k = − |
А |
и b = − |
C |
. |
|
|
|
|||||
|
|
B |
|
B |
||
Пусть прямая пересекает ось oy в точке P(0,b).
Из уравнения прямой, проходящей через две точки, имеем
y − y1 = y2 − y1 (x − x1) . x2 − x1
,Отсюда
y2 − y1 =tgα = k . x2 − x1
Таким образом y − y1 = k(x − x1).
Уравнение полученной прямой принимает вид уравнения прямой с угловым коэффициентом k, если b=y1 - k x1.
2.5. Уравнение прямой в отрезках
Общее уравнение прямой Ax+By+C=0 может быть преобразовано к виду уравнения прямой “в отрезках”: ax + by =1.
Прямая в отрезках пересекает ось ox в точке А(а,0) и ось oy в точке В(0,b).
8
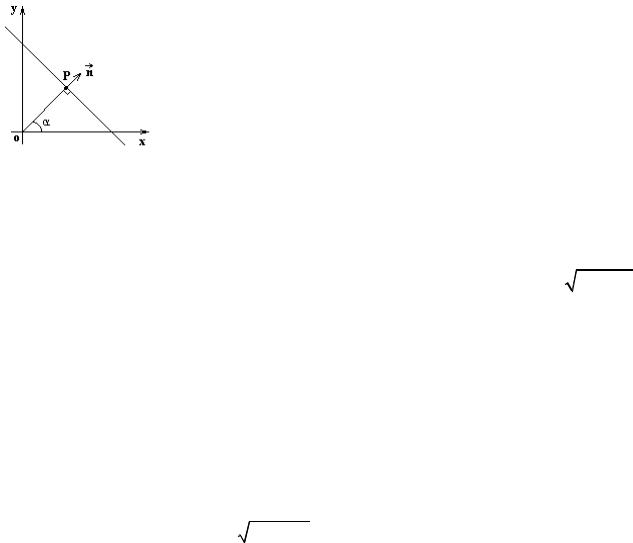
2.6. Нормальное уравнение прямой
Пусть известно расстояние от прямой до начала координат |
|||
|
OP |
= p и угол |
α между перпендикуляром к прямой и |
|
|
|
|
осью ox. Из |
нормального уравнения плоскости в |
||
пространстве, полагая z=0 и учитывая, что |
|
|
|
π |
|
|
|
cos |
−α = sin α, |
|
|
2 |
|
|
|
получаем нормальное уравнение прямой на плоскости в |
|||
виде |
|
|
|
xcosα + ysin α − p = 0 . |
|
|
|
Нормальное уравнение прямой можно получить из общего уравнения |
|||
прямой Ax+By+C=0, умножив его на нормирующий множитель µ = ± |
1 |
. |
|
A2 + B2 |
|||
Знак числа µ должен быть противоположен знаку числа С.
Косинусы углов, образуемых прямой с осями координат, называются
направляющими косинусами прямой.
Если угол между прямой и осью ox равен α и угол между прямой и осью oy равен β, то cos2 α + cos2 β =1.
2.7. Расстояние от точки до прямой
Расстояние d от точки M0(x0,y0) до прямой, задаваемой нормальным уравнением, равно модулю отклонения точки от прямой δ , d=|δ |, где
δ = x0 cosα + y0 sin α − p = ± Ax0 +2By0 +2 C .
A + B
По этой формуле δ положительно, если точка М0 и начало координат лежат по разные стороны от прямой, в противном случае δ отрицательно.
2.8. Координаты точки пересечения двух прямых
Если прямые заданы уравнениями A1x+B1y+C1=0 и A2x+B2y+C2=0, то координаты точки их пересечения (x0, y0) получаются как решение системы уравнений
A1x + B1 y +C1 = 0,A2 x + B2 y +C2 = 0
|
|
|
B1 |
C1 |
|
|
|
|
|
C1 |
A1 |
|
|
|
A1 |
B1 |
|
по формулам Крамера в виде x = |
|
|
B2 |
C2 |
|
|
, y = |
|
|
C2 |
A2 |
|
|
, при |
≠ 0. |
||
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
0 |
|
|
A1 |
B1 |
0 |
|
|
A1 |
B1 |
|
|
|
A2 |
B2 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
А2 |
B2 |
|
|
|
|
|
A2 |
B2 |
|
|
|
|
|
|
9
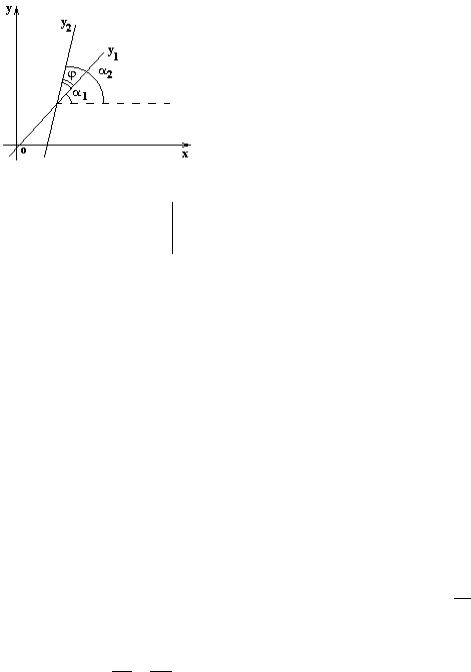
Отсюда tgϕ = |
|
k2 − k1 |
||
1+ k k |
||||
|
||||
|
2 |
1 |
||
2.9. Угол между двумя прямыми
Пусть две прямые заданы уравнениями: y1 = k1x +b1,
y2 = k2 x +b2.
Острый угол ϕ пересечения этих прямых (отсчитываемый против часовой стрелки) находится из следующих соотношений:
tgϕ = tg(α2 − α1 ) = |
|
tgα2 −tgα1 |
|
. |
|
1 + tgα1tgα2 |
|||||
|
|
||||
.
Если прямые заданы общими уравнениями А1x+B1y+C1=0 и A2x+B2y+C2=0, то угловые коэффициенты прямых равны
tgα = − |
A1 |
, |
tga |
2 |
= − |
A2 |
|
|||
|
|
|
||||||||
1 |
B1 |
|
|
|
|
B2 |
||||
|
|
|
|
|
|
|||||
и угол ϕ между прямыми определяется формулой |
||||||||||
tgϕ = |
|
A1B2 − A2 B1 |
|
. |
||||||
|
|
|||||||||
|
A A + B B |
|||||||||
|
|
|
||||||||
|
|
1 |
2 |
1 |
2 |
|
|
|
|
|
2.10. Условие параллельности и перпендикулярности двух прямых |
||||||||||
Прямые y1=k1x+b1 и y2=k2x+b2 |
параллельны друг другу, если ϕ = 0 . |
|||||||||
Следовательно, tgϕ = 0, то есть k1=k2. |
|
|
|
|
|
|
|
|||
Прямые y1=k1x+b1 и y2=k2x+b2 перпендикулярны друг другу, если ϕ= π2 .
Следовательно, tgϕ→∞, то есть k1k2 = -1. Отсюда k1 = − 1 . k2
Если прямые заданы общими уравнениями:
А1В1-А2В1=0, A1 = A2 - условие параллельности,
B1 B2
А1А2+В1В2=0 - условие перпендикулярности прямых.
2.11. Уравнение пучка прямых
Совокупность всех прямых плоскости, проходящих через некоторую точку M(x0,y0), называется пучком прямых с центром М.
Пусть A1x+B1y+C1=0 и A2x+B2y+C2=0 - уравнения двух прямых, пересекающихся в точке М; α и β - произвольные числа, одновременно не равные нулю, тогда
α (A1x+B1y+C1)+β(A2x+B2y+C2)=0 - уравнение прямой, проходящей через точку М.
10
