
- •Федеральное агентство по образованию РФ
- •АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ
- •ТЕОРЕТИЧЕСКИЕ ОСНОВЫ АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ НА ПЛОСКОСТИ
- •1.ПРОСТЕЙШИЕ ЗАДАЧИ НА ПЛОСКОСТИ
- •1.1. Расстояние между двумя точками
- •1.2. Деление отрезка в данном отношении
- •1.3. Площадь треугольника
- •2. ПРЯМАЯ ЛИНИЯ НА ПЛОСКОСТИ
- •2.1. Общее уравнение прямой
- •2.2. Каноническое уравнение прямой
- •2.3. Уравнение прямой, проходящей через две точки
- •2.5. Уравнение прямой в отрезках
- •2.6. Нормальное уравнение прямой
- •2.7. Расстояние от точки до прямой
- •2.8. Координаты точки пересечения двух прямых
- •2.9. Угол между двумя прямыми
- •2.11. Уравнение пучка прямых
- •3. КРИВЫЕ ВТОРОГО ПОРЯДКА
- •3.1. Эллипс
- •3.2. Окружность
- •3.3. Гипербола
- •3.4. Парабола
- •4. ПРЕОБРАЗОВАНИЯ КООРДИНАТ
- •4.1. Параллельный перенос
- •4.2. Поворот координатных осей
- •4.3. Изменение начала координат и поворот осей
- •5. ЛИНИИ В ПОЛЯРНОЙ СИСТЕМЕ КООРДИНАТ
- •5.1. Полярные координаты на плоскости
- •5.2. Связь полярных координат с декартовыми
- •5.3.1. Кривые второго порядка
- •5.3.2. Спирали
- •5.3.3. Розы
- •6. ПАРАМЕТРИЧЕСКОЕ ЗАДАНИЕ ЛИНИЙ
- •6.1. Окружность
- •6.2. Циклоида
- •6.3. Астроида
- •7. КРИВЫЕ ТРЕТЬЕГО ПОРЯДКА
- •7.1. Полукубическая парабола
- •7.2. Локон Аньези
- •7.3. Декартов лист
- •8. КРИВЫЕ ЧЕТВЕРТОГО ПОРЯДКА
- •8.1. Улитка Паскаля
- •8.2. Кардиоида
- •8.3. Лемниската Бернулли
- •Парабола
- •РЕШЕНИЕ ЗАДАЧ ПО АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ НА ПЛОСКОСТИ
- •ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ
- •Вариант 1
- •ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА
- •1. Поверхности
- •1.1. Линейчатые поверхности
- •1.2. Поверхности вращения
- •1.3. Поверхности второго порядка
- •2.1. Эллипсоид
- •2.2. Гиперболоиды
- •2.2.1. Однополостный гиперболоид
- •2.2.2. Двуполостный гиперболоид
- •2.3. Параболоиды
- •2.3.1. Эллиптический параболоид
- •2.4. Конус
- •2.5. Цилиндры
- •2.5.1. Эллиптический цилиндр
- •2.5.2. Гиперболический цилиндр
- •2.5.3. Параболический цилиндр
- •РЕШЕНИЕ ТИПИЧНЫХ ЗАДАЧ
- •ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ
- •БИБЛИОГРАФИЧЕСКИЙ СПИСОК

ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ
Вариант 1
1.Найти нижеперечисленные элементы треугольника:
а) уравнения и длины сторон; б) уравнения высот; в) уравнения медиан; г) центр тяжести;
д) центр и радиус описанного круга; е) внутренние углы,
если даны три вершины треугольника: А(0, 0); В(10, -5); С(6, 3).
|
|
|
|
|
Ответ: а)АВ: х + 2у = 0, |
АВ = 5 5 , |
|||
ВС: 2х + у – 15 = 0, ВС = 4 |
5 |
, |
||
АС: х – 2у = 0, |
АС = 3 |
|
; |
|
5 |
||||
б) х – 2у = 0 |
(из А), |
|||
2х + у – 15 = 0 |
|
(из В), |
||
2х – у – 9 = 0 |
|
(из С); |
||
в) х + 8у = 0 |
(из А), |
|||
13х + 14у – 60 = 0 |
(из В), |
|||
11х – 2у – 60 = 0 (из С); г) (16/3, -2/3);
д) (5, -5/2), R = (5 
 5 )/2;
5 )/2;
е) tgA = 4/3, tgB = 3/4, C = π/2.
2. Построить кривую 5х2 + 9у2 – 30х + 18у + 9 = 0.
Ответ: (x −93)2 + ( y +51)2 =1.
3.Составить уравнение параболы, вершина которой находится в начале координат, зная, что парабола расположена симметрично относительно оси Ох и проходит через точку А(9; 6).
Ответ: у2 = 4х.
4. Фокусы гиперболы совпадают с фокусами эллипса |
x2 |
+ |
y2 |
=1. Составить |
|||||
25 |
9 |
||||||||
уравнение гиперболы, если ее эксцентриситет е = 2. |
|
|
|||||||
|
|
|
|
||||||
Ответ: |
x2 |
− |
y2 |
=1. |
|
|
|
|
|
4 |
12 |
|
|
|
|
||||
|
|
|
|
|
|
|
|||
5. Даны две точки М1(9; -3) и М2(-6; 5). Начало координат перенесено в точку М1, а оси координат повернуты так, что положительное направление новой
оси абсцисс совпадает с направлением отрезка M1M 2 . Вывести формулы преобразования координат.
52

|
|
|
15 ′ |
8 |
|
′ |
|
|
|
8 |
′ |
15 |
′ |
|
|
||||
Ответ: x = − |
17 x − |
|
y |
|
+9, |
|
y |
= |
|
x |
−17 y |
|
−3. |
|
|||||
17 |
|
17 |
|
|
|||||||||||||||
6. |
Поворотом осей координат на угол α преобразовать уравнение и построить |
||||||||||||||||||
|
кривую, если sinα = -2/ |
|
|
(-π/2 < α < 0), 6x2 – 4xy + 9y2 = 10. |
|||||||||||||||
|
5 |
|
|||||||||||||||||
Ответ: эллипс х′2 + у′2/2 = 1. |
|
|
|
|
|
|
|
|
|||||||||||
7. |
Привести кривые к каноническому виду: |
|
|
||||||||||||||||
|
а) 5 x2 + |
|
3 |
xy + |
7 y2 |
= 0, |
|
|
|
|
|
|
|
|
|
|
|||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|||||||
|
4 |
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
б) x2 + y2 + 2x + 4y + 10 = 0. |
|
|
|
|
|
|
|
|
||||||||||
Ответ: а) α = -30°, х2 + 2у2 = 0; |
|
|
|
|
|
|
|
|
|||||||||||
|
б) (х + 1)2 + (у + 2)2 + 5 = 0. |
|
|
|
|
|
|
||||||||||||
8. |
Какая линия задается уравнением ρ = |
|
|
9 |
? |
||||||||||||||
5 − 4cosϕ |
|||||||||||||||||||
Ответ:
5
0 |
5 |
10 |
-5
53

Вариант 2
1.Найти нижеперечисленные элементы треугольника:
а) вершины треугольника; б) длины сторон; в) уравнения высот; г) уравнения медиан;
д) центр и радиус описанного круга; е) центр тяжести; ж) внутренние углы,
если даны уравнения трех сторон треугольника:
АС: х – 2у – 1 = 0, АВ: х + 2у + 3 = 0, ВС: 2х + у + 18 = 0.
Ответ: а) А(-1, -1), В(-11, 4), С(-7, -4); б) АВ = 5 
 5 , ВС = 4
5 , ВС = 4 
 5 , АС = 3
5 , АС = 3 
 5 ;
5 ;
в) х – 2у – 1 = 0 |
(из А), |
2х + у + 18 = 0 |
(из В), |
2х – у + 10 = 0 |
(из С); |
г) х + 8у + 9 = 0 |
(из А), |
13х + 14у + 87 = 0 (из В), 11х – 2у + 63 = 0 (из С);
д) (-6, 3/2), R = (5 5 )/2; е) (-19/3, -1/3);
ж) tgA = 4/3, tgB = 3/4, C = π/2.
2.Построить кривую х = 2у2 – 12у + 14.
Ответ: х + 4 = 2(у – 3)2.
3.Составить уравнение гиперболы, фокусы которой лежат на оси абсцисс симметрично относительно начала координат, если даны точки М1(6; -1) и М2(-8; 2 2 ) гиперболы.
Ответ: |
x2 |
|
− |
|
y2 |
=1. |
32 |
|
8 |
||||
|
|
|
|
|||
4. Эллипс |
|
касается оси абсцисс в точке А (3, 0) и оси ординат в точке |
||||
В(0, -4). Составить уравнение этого эллипса, зная, что его оси симметрии параллельны координатным осям.
Ответ: (x −3)2 + ( y + 4)2 =1. 9 16
5. Даны две точки М(3; 1) и N(-1; 5). Найти их координаты в новой системе координат, если исходные оси координат повернуты на угол -45°.
Ответ: М( 
 2 , 2
2 , 2 
 2 ), N(-3
2 ), N(-3 
 2 , 2
2 , 2 
 2 ).
2 ).
54

6. |
Поворотом осей координат на угол α преобразовать уравнение и постро-ить |
||||||||||||
|
кривую, если sinα = -2/ |
|
|
(-π/2 < α < 0), 32x2 + 52xy – 7y2 + 180 =0. |
|||||||||
|
|
5 |
|||||||||||
Ответ: гипербола |
x |
′2 |
− |
y |
′2 |
=1. |
|||||||
|
|
|
|
|
|||||||||
|
|
9 |
|
|
|
4 |
|
|
|
||||
7. |
Привести кривые к каноническому виду: |
||||||||||||
|
а) 5 x2 − |
3 |
xy + |
7 y2 |
+1 = 0, |
||||||||
|
2 |
||||||||||||
|
4 |
|
|
4 |
|
|
|
|
|
|
|
||
б) x2 + y2 – 2x + 4y + 1 = 0. Ответ: а) α = 30°, х2 + 2у2 = -1;
б) (х - 1)2 + (у + 2)2 = 4.
8. Какая линия задается уравнением ρ = 1−cos3 ϕ?
Ответ:
Вариант 3
1.Найти нижеперечисленные элементы треугольника:
а) вершины треугольника; б) уравнения и длины сторон; в) уравнения высот; г) уравнения медиан;
д) центр и радиус описанного круга; е) центр тяжести; ж) внутренние углы,
если даны две вершины треугольника: А(1, 1); В(21, -9) и точка пересечения высот К(13, 7).
Ответ: а) С(13, 7); |
|
|
|
|
|
б) АВ: х + 2у – 3 = 0, |
АВ = 10 |
|
|
, |
|
5 |
|||||
ВС: 2х + у – 33 = 0, |
ВС = 8 |
|
, |
|
|
5 |
|
||||
АС: х – 2у + 1 = 0, |
АС = 6 |
|
; |
||
5 |
|||||
в) х – 2у + 1 = 0 |
(из А), |
|
|
|
|
55

2х + у – 33 = 0 |
(из В), |
2х – у – 19 = 0 |
(из С); |
г) х + 8у – 9 = 0 |
(из А), |
13х + 14у – 147 = 0 (из В), 11х – 2у – 129 = 0 (из С);
д) (11, -4), R = 5 
 5 ; е) (35/3, -1/3);
5 ; е) (35/3, -1/3);
ж) tgA = 4/3, tgB = 3/4, C = π/2.
2.Построить кривую 4х = -у2 + 4у.
Ответ: 4(х – 1) = -(у – 2)2.
3.Составить уравнение гиперболы, фокусы которой лежат на оси абсцисс симметрично относительно начала координат, если даны точка М1(-5; 3)
гиперболы и эксцентриситет ε = 
 2 .
2 .
Ответ: х2 – у2 = 16.
4.Точка С (-3, 2) является центром эллипса, касающегося обеих координатных осей. Составить уравнение этого эллипса, зная, что его оси симметрии параллельны координатным осям.
Ответ: (x +93)2 + ( y −42)2 =1.
5. Оси координат повернуты на угол α = |
60°. Известны координаты точек |
||||||||||||||||||||||||
|
А(2 3 ;-4), В( 3 ;0) в новой системе координат. Вычислить координаты этих |
||||||||||||||||||||||||
|
точек в старой системе координат. |
|
|
||||||||||||||||||||||
Ответ: А(3 3 , 1), В( 3 /2, 3/2). |
|
|
|||||||||||||||||||||||
6. |
Поворотом осей координат на угол α преобразовать уравнение и построить |
||||||||||||||||||||||||
|
кривую, если sinα = 2/ |
5 |
|
|
(0 < α < π/2), |
17x2 – 12xy + 8y2 = 0. |
|||||||||||||||||||
Ответ: вырожденный эллипс х′2 + 4у′2 = 0 – точка (0, 0). |
|||||||||||||||||||||||||
7. |
Привести кривые к каноническому виду: |
|
|||||||||||||||||||||||
|
а) 5х2 – (2 3 )ху + 7у2 – 4 = 0, |
|
|
||||||||||||||||||||||
|
б) х2 + 7у + 2х + 2 = 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Ответ: а) α = 30°, х2 + 2у2 = 1; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
б) (х + 1)2 = -7(у + 1/7). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
8. |
Какая линия задается уравнением sinρ = 1/2 ? |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
-10 |
|
|
|
-5 |
|
|
|
|
|
5 |
|
|
10 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-5 |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
π |
+ 2πn, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Ответ: ρ = |
6 |
+ 2πk. |
|
|
|
|
|
-10 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
5π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
56

Вариант 4
1.Найти нижеперечисленные элементы треугольника: а) вершины треугольника; б) уравнения и длины сторон; в) уравнения высот; г) уравнения медиан;
д) центр и радиус описанного круга; е) центр тяжести; ж) внутренние углы,
если дана вершина треугольника А(-1, -1) и две высоты
|
|
|
|
|
|
|
|
|
|
|
|
|
2х + у – 27 = 0 и 2х – у – 17 = 0. |
||
Ответ: а) В(19, -11), С(11, 5); |
|
||||||||||||||
|
б) АВ: х + 2у + 3 = 0, |
АВ = 10 5 , |
|||||||||||||
|
|
ВС: 2х + у – 27 = 0, |
ВС = 8 5 , |
||||||||||||
|
|
АС: х – 2у – 1 = 0, |
|
АС = 6 5 ; |
|||||||||||
|
в) х – 2у – 1 = 0 |
|
|
|
|
(из А), |
|
||||||||
|
|
2х + у – 27 = 0 |
|
|
|
|
(из В), |
|
|||||||
|
|
2х – у – 17 = 0 |
|
|
|
|
(из С); |
|
|||||||
|
г) х + 8у + 9 = 0 |
|
|
|
|
(из А), |
|
||||||||
|
|
13х + 14у – 93 = 0 |
|
(из В), |
|
||||||||||
|
|
11х – 2у – 111 = 0 |
(из С); |
|
|||||||||||
|
д) (9, -6), |
R = 5 |
|
; |
|
|
|
|
|||||||
|
5 |
|
|
|
|||||||||||
|
е) (29/3, -7/3); |
|
|
|
|
|
|
||||||||
|
ж) tgA = 4/3, tgB = 3/4, C = π/2. |
||||||||||||||
2. |
Построить кривую x = −2 −5 −6y − y2 . |
||||||||||||||
Ответ: часть эллипса |
|
x2 |
|
+ |
( y +3)2 |
=1, х ≤ 0, y [−5,−1]. |
|||||||||
16 |
|
4 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
3. Составить уравнение параболы, если дан фокус F(6, 0) и уравнение |
|||||||||||||||
|
директрисы х + 6 = 0. |
|
|
|
|||||||||||
Ответ: 24х = у2. |
|
|
|
|
|
|
|
|
|||||||
4. |
Составить |
уравнение |
гиперболы, если известны ее эксцентриситет |
||||||||||||
|
е = 13/12, фокус F(0, 13) и уравнение директрисы 13у – 144 = 0. |
||||||||||||||
Ответ: |
|
x2 |
− |
|
y |
2 |
= −1. |
|
|
|
|
|
|
||
25 |
144 |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||
5. |
Определить координаты точки О′ нового начала координат, если точка |
||||||||||||||
А(3, -4) лежит на новой оси абсцисс, а точка В(2, 3) лежит на новой оси ординат, причем оси старой и новой систем координат имеют соответственно одинаковые направления.
Ответ: О′(2, -4).
6.Поворотом осей координат на угол α преобразовать уравнение и построить кривую sinα = 4/5 ( 0 < α < π/2),
57

16x2 – 24xy + 9y2 – 160х + 120у + 425 = 0.
Ответ: пара мнимых прямых (у′2 + 4)2 + 1 = 0; для (х, у) R. 7. Привести кривые к каноническому виду:
а) 14 x2 − 323 xy − 54 y2 −1 = 0, б) х2 – 11у + 2х + 4 = 0.
Ответ: а) α = -30°, х2 – 2у2 = 1; б) (х + 1)2 = 11(у – 3/11).
8. Какая линия задается уравнением ρ = а (1 – cosϕ)? Ответ:
Вариант 5
1.Найти нижеперечисленные элементы треугольника:
а) вершины треугольника; б) уравнения и длины сторон; в) уравнения высот; г) уравнения медиан;
д) центр и радиус описанного круга; е) центр тяжести; ж) внутренние углы,
если даны две вершины треугольника: А(-1, 2), В(9, -3) и точка пересечения медиан М(13/3, 4/3).
Ответ: а) С(5, 5); |
|
б) АВ: х + 2у – 3 = 0, |
АВ = 5 5 , |
ВС: 2х + у – 15 = 0, |
ВС = 4 5 , |
АС: х – 2у + 5 = 0, |
АС = 3 5 ; |
в) х – 2у + 5 = 0 |
(из А), |
2х + у – 15 = 0 |
(из В), |
2х – у – 5 = 0 |
(из С); |
г) х + 8у – 15 = 0 |
(из А), |
13х + 14у – 75 = 0 |
(из В), |
11х – 2у – 45 = 0 (из С); д) (4, -1/2), R = (5 
 5 )/2;
5 )/2;
е) (13/3, 4/3);
ж) tgA = 4/3, tgB = 3/4, C = π/2.
58
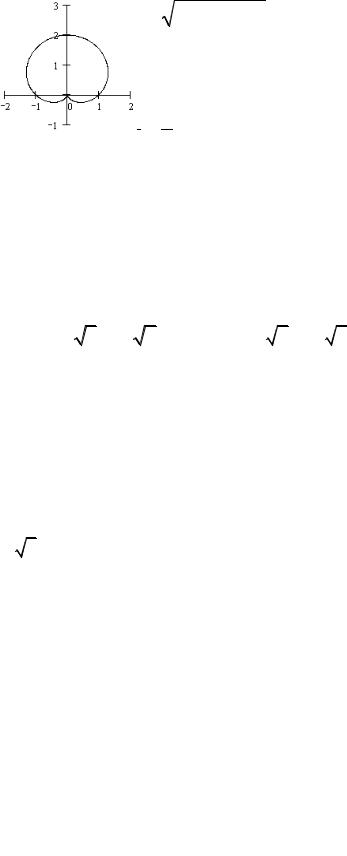
2. Построить кривую: x = 5 − |
3 |
y2 + 4y −12. |
|||
|
|
4 |
|
|
|
Ответ: часть гиперболы |
(x −5)2 |
|
( y + 2)2 |
|
|
9 |
|
− |
16 |
= −1, x ≤ 5, y (−∞,−6] [2,∞). |
|
3.Составить уравнение эллипса, фокусы которого расположены на оси абсцисс симметрично относительно начала координат, если даны две точки эллипса: М1(2; 0) и М2( 
 2 ,
2 , 
 2 /2).
2 /2).
Ответ: х2/4 + у2 = 1.
4. Определить |
координаты точек пересечения эллипса |
|
x2 |
+ |
y2 |
=1 и |
|
100 |
225 |
||||||
параболы 24х = у2. |
|
|
|||||
|
|
|
|
|
|||
Ответ: (6, 12), |
(6, -12). |
|
|
|
|
|
|
5.Определить старые координаты нового начала и угол α, на который повернуты оси, если формулы преобразования координат заданы
равенствами: x = |
2 |
′ |
+ |
2 |
y |
′ |
+5; |
y = − |
2 |
′ |
+ |
2 |
y |
′ |
−3. |
|
2 |
2 |
2 |
2 |
|||||||||||||
x |
|
x |
|
Ответ: О′(5, -3), α = -45°.
6.Поворотом осей координат на угол α преобразовать уравнение и построить кривую, если sinα = -3/5 (π < α < (3/2) π),
9x2 – 24xy + 16y2 –20х + 110у – 50 = 0.
Ответ: парабола 2(х′+ 3) = (у′– 2)2.
7. Привести кривые к каноническому виду:
а) 14 x2 + 323 xy − 54 y2 = 0, б) х2 + 2у2 + 2х + 4у = 6.
Ответ: а) α = 30°, х2 – 2у2 = 0; б) (х + 1)2 + 2(у + 1)2 = 9.
8. Какая линия задается уравнением ρ = а(1 + sinϕ)? Ответ:
59

РАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА «ЛИНИИ НА ПЛОСКОСТИ» Задача 1 Построить алгебраические кривые в декартовой системе координат. 1.1. Прямая Ах + Ву + С = 0.
1.2. |
Эллипс |
x2 |
+ |
y2 |
|
=1. |
|||||
a2 |
b2 |
||||||||||
|
|
|
|
|
|
|
|||||
1.3. |
Гипербола |
|
x2 |
− |
|
y2 |
=1. |
||||
|
a2 |
|
b2 |
||||||||
|
|
|
|
|
|
|
|
||||
1.4.Парабола у2 = 2рх.
1.5.Полукубическая парабола а2х3 – у2 = 0.
1.6.Верзиера (локон Аньези) (х2 + а2)у – а3 = 0, а > 0.
1.7.Декартов лист х3 + у3 – 3аху = 0, а > 0.
1.8.Циссоида х3 + (х – а)у2 = 0, а > 0.
1.9.Строфоида (х + а)х2 + (х – а)у2 = 0, а > 0.
Конхоида Никомеда (конхоида прямой х = а).
Рассмотреть случаи:
1.10.(x - a)2(x2 + y2) – l2x2 = 0, 0 < l <a,
1.11.(x - a)2(x2 + y2) – l2x2 = 0, 0 < a < l,
1.12.(x - a)2(x2 + y2) – l2x2 = 0, 0 < a = l.
Улитка Паскаля (конхоида окружности). Рассмотреть случаи:
1.13.(x2 + y2 – ax)2 – l2(x2 + y2) = 0, 0 < 2a ≤ l,
1.14.0 < a < l < 2a и a > l.
1.15.Кардиоида (x2 + y2 + 2ax)2 = 4a2(x2 + y2), 0 < a = l.
Овалы Кассини (х2 + у2)2 – 2с2(х2 – у2) – (а4 – с4) = 0.
Рассмотреть случаи:
1.16. |
0 |
< c 2 < a, |
|
1.17. |
0 |
< c < a < c |
2 , |
1.18.0 < a < c.
1.19.Частный случай, лемниската Бернулли, 0 < a = c,
|
|
(х2 + у2)2 – 2а2(х2 – у2) = 0. |
|||
1.20. Обыкновенная циклоида |
) |
|
|||
acos |
|
(x + 2ay − y2 |
= a − y, a > 0 . |
||
|
a |
|
|||
|
|
||||
|
|
|
|
||
|
|
|
|
|
|
1.21. Астроида х2/3 + у2/3 = b2/3.
Подэры кривой Штейнера, имеющие уравнение
60
(x2 + y2)2 + [(a + 3r) y2 + (a – r) x2] x = 0.
Рассмотреть случаи:
1.22. а = 0 трехлепестковая роза (х2 + у2)2 + rx(3у2 – х2) = 0, 1.23. a = r прямой двулистник (х2 + у2)2 + 4rу2х = 0,
1.24. a = -r прямой трилистник (х2 + у2)2 + 2rx(у2 – х2) = 0.
Задача 2 Построить кривую, заданную параметрически.
2.1. x = a cos t |
, |
эллипс, |
0 ≤ t ≤ 2π. |
|
|
y = b sin t |
|
||
|
|
|
|
|
2.2.x = acht,
гипербола, − ∞ < t < +∞.
y = asht
2.3.x = t,
парабола, − ∞ < t < +∞.
y = at 2
2.4.x = at + b,
прямая, − ∞ < t < +∞.
y = ct + d
2.5.x =t2 , полукубическая парабола,
y = at3 −∞< t < +∞.
2.6. |
x = a cos3 t, |
астроида, |
0 ≤t ≤ 2π. |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|||
|
y = asin3 t |
|
|
|
|
|
||||||
|
|
|
3at |
|
|
|
Декартов лист |
|
|
|||
2.7. |
x = |
|
|
|
, |
|
|
|||||
1+t |
3 |
|
|
|||||||||
|
|
|
|
|
|
−1< t < +∞. |
|
|
||||
|
|
|
3at2 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|||||
|
y = |
|
|
|
|
, |
|
−1< t < +∞. |
|
|
||
|
1+t |
3 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|||
2.8. |
x = a(t −sin t), |
a > 0, |
циклоида прямой. |
|||||||||
|
|
|
|
|
|
|
|
|
−∞< t < +∞ |
|||
|
y = a(1−cost), |
|
|
|||||||||
Трохоиды (циклоиды прямой): |
|
|
||||||||||
2.9. |
Удлиненнаяциклоида x |
= a(t −λsin t), |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
= a(1−λcost), |
λ >1. |
|
|
|
|
|
|
|
|
|
|
y |
|||
2.10. Укороченнаяциклоида x = a(t −λsin t), |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
λ <1. |
|
|
|
|
|
|
|
|
|
y = a(1−λcost), |
|||
Циклоиды окружности: |
|
|
|
|
||||||||
2.11. Эпициклоиды x = (R + mR)cos mt −mR cos(t + mt), |
||||||||||||
|
m > 0 |
|
|
|
|
|
= (R + mR)sin mt −mRsin(t + mt), |
|||||
|
|
|
|
|
y |
|||||||
а) m = 2, 3, 4, 5…,
б) m = 3/2, 3/5, … 1/3, 1/4, …,
61
в) m – иррациональное.
2.11. Гипоциклоиды x = (R + mR)cos mt −mR cos(t + mt), |
|
m < 0 |
|
y = (R + mR)sin mt −mRsin(t + mt), |
|
а) |m| = 2, 3, 4, 5…,
б) |m| = 3/2, 3/5, … 1/3, 1/4, …,
в) |m| – иррациональное. Трохоиды циклоиды окружности
x = (R + mR)cos mt − hcos(t + mt), h ≠ mR,
y = (R + mR)sin mt − hsin(t + mt).
2.13. h < mR, m > 0 укороченная эпициклоида, 2.14. h > mR, m > 0 удлиненная эпициклоида, 2.15. h < mR, m < 0 укороченная гипоциклоида, 2.16. h > mR, m < 0 удлиненная гипоциклоида. Частные случаи циклоид:
2.17. Трохоидальные розы, h = R + mR,
x = (R + mR)cos mt −(R + mR)cos(t + mt),y = (R + mR)sin mt −(R + mR)sin(t + mt).
2.18. Улитка Паскаля (эпициклоида при R = r, h – любое)
x = 2r cost − hcos2t,y = 2r sin t − hsin 2t.
2.19. Эллипс (гипоциклоида при R = 2r)
x = (R / 2 + h)cos(t / 2),y = (R / 2 − h)sin(t / 2).
2.20. Кардиоида (эпициклоида при |m| = 1, одна из улиток Паскаля)
x = 2r cost − r cos2t,y = 2r sin t − r sin 2t.
2.21. Кривая Штейнера (гипоциклоида при |m| = 1/3)
x = 2r cos(t /3) + r cos(2t /3),y = 2r sin(t /3) − r sin(2t /3).
2.22. Астроида (гипоциклоида при |m| = 1/4)
x = Rcos3 (t /3),
y = Rsin3 (t /3).
2.23. Конхоида Никомеда (конхоида прямой х = а)
62

x = a(1+λcost), |
− |
π |
<t < |
π |
и |
π |
< t < |
3π |
. |
|
|
||||||||||
2 |
2 |
2 |
2 |
|||||||
y = a(tgt +λsin t), |
|
|
|
|
|
|||||
λ = 2,1 2…, |
|
праваяветвь |
леваяветвь |
|||||||
2.24. |
x =t, |
|
|
Верзиера (локонАньези) |
||
|
|
|
3 |
|
||
|
|
|
a |
|
,a > 0. |
|
|
|
|
|
|||
|
y = |
|
|
|
||
|
t |
3 |
|
3 |
||
|
|
+ a |
|
|
||
Задача 3 Построить кривые в полярной системе координат.
3.1. |
ρ = |
|
p |
|
|
|
прямая, α-уголмеждуполярной |
|
|
cos(ϕ−α) |
|
осьюинормальюккривой. |
|||||
Кривые II порядка. |
||||||||
3.2. ρ = |
|
p |
|
, |
e >1гипербола, e =1 парабола, e <1 эллипс. |
|||
|
1+ecosϕ |
|||||||
Конхоида Никомеда (конхоида прямой х = а). |
||||||||
3.3. ρ = |
|
a |
|
−l |
леваяветвь, |
|||
|
cosϕ |
|||||||
|
|
|
|
|
|
|
||
|
ρ = |
|
a |
|
+l |
праваяветвь. |
||
|
|
cosϕ |
||||||
|
|
|
|
|
|
|
||
Рассмотреть случаи: 0 < l < a, 0 < l = a, 0 < a < l.
Окружность:
3.4.ρ = a cosϕ и ρ = a sinϕ.
Конхоиды окружности a cosϕ + l: 3.5.0 < 2a ≤ l,
3.6.0 < a < l < 2a, 3.7.0 < l < a,
3.8.ρ = a(1 + cosϕ) – кардиоида – частный случай конхоиды окружности.
Синусоидальные спирали
ρm = amcosmϕ или ρm = amsinmϕ
при m – рациональном – алгебраические линии того или иного порядка. 3.9.m = 1, ρ = a cosϕ - окружность,
m= -1, ρ = a/cosϕ - прямая,
3.10.m = 2, ρ2 = a2 cos2ϕ- лемниската Бернулли,
m= -2, ρ = a2/cos2ϕ- равносторонняя гипербола,
3.11. m = 1/2, ρ = a cos2(ϕ/2)- кардиоида, m = -1/2, ρ = 2a/(1+cosϕ)- парабола.
63

Овалы Кассини: ρ2 = c2 cos2ϕ± c4 cos2 2ϕ+(a4 −c4 ):
3.12.0 < c 
 2 < a,
2 < a,
3.13.0 < c < a < 
 2 , 3.14.0 < a < c,
2 , 3.14.0 < a < c,
3.15.0 < c = a, ρ = a 2cos2ϕ - частный случай, лемниската Бернулли.
Подэры кривой Штейнера имеют уравнение ρ = 4r cos3ϕ – (a + 3r) cosϕ.
3.16.3/a = 0, ρ = r cos3ϕ |
- трехлепестковая роза, |
|
3.17. a = r, ρ = -4r cosϕ sin2ϕ |
- прямой двулистник, |
|
3.18.a = -r, ρ = 2r cosϕ cos2ϕ |
- прямой трехлистник, |
|
3.19.a = -3r, ρ = 4r cos3ϕ |
- однолистник. |
|
Подэра астроиды. |
|
|
3.20. ρ = (R/2) cos2ϕ – c cosϕ - |
«жук», |
|
(при с = 0 – роза). |
|
|
3.21.Розы, или кривые Гвидо Гранди ρ = a sinkϕ, a > 0, k > 0. Рассмотреть случаи:
1)k – целое четное, нечетное;
2)k – рациональное;
3)k – иррациональное.
Розы относятся к трохоидам. 3.22.Узлы, ρ = a ctgkϕ.
Рассмотреть случаи: k = 1 «каппа»;
k = 2 «ветряная мельница»; k = 1/2 строфоида.
3.23.Кривые, полученные Хабеннихтом:
ρ= 4 (1 + cos3ϕ) + 4 sin23ϕ - лист щавеля,
ρ= 4 (1 + cos3ϕ) – 4 sin23ϕ - лист трилистника,
ρ= 3 (1 + cos2ϕ) + 2 cosϕ + sin2ϕ – 2 sin23ϕ cos4(ϕ/2) - лист плюща.
3.24.Спирали:
ρ= a ϕ - спираль Архимеда,
ρ= a/ϕ - гиперболическая спираль,
ρ= a/ϕ + l - конхоида гиперболической спирали,
ρ= a ϕ2 – l, - спираль Галилея,
l > 0, l = 0
ρ = a ϕ - спираль Ферма,
64

ρ = a ϕ + l- параболическая спираль, l > 0,
ρ = a/ ϕ |
- «жезл», |
ρ = aϕ |
- логарифмическая спираль, а > 0. |
Тест
Укажите название кривой II порядка на плоскости x2 + 2x − y2 = 4:
а) эллипс; б) окружность; в) пара параллельных прямых; г)точка; д) круг; е) эллиптический параболоид; ж) парабола; з) гипербола; и) лист Декарта; к) пара параллельных плоскостей.
Правильный ответ: Ответ: з).
65
