вращение вокруг оси O z : |
F (x, y, z)= L(± |
x2 |
+ y2 , z)= 0 |
; |
3) кривая L(y, z)= 0 , лежащая в плоскости Oyz ; |
x2 + z2 )= 0 |
|
||
вращение вокруг оси Oy : |
F (x, y, z)= L(y,± |
, |
||
вращение вокруг оси O z : |
F (x, y, z)= L(± |
x2 |
+ y2 , z)= 0 |
; |
1.3. Поверхности второго порядка
Алгебраической поверхностью второго порядка называется поверхность
S , уравнение которой в декартовой системе координат имеет вид a11x2 + a22 y2 + a33 z2 + 2a12 xy + 2a13 xz + 2a23 yz +
+2a14 x + 2a24 y + 2a34 z + a44 = 0,
(5)
где не все коэффициенты при членах второго порядка равны одновременно нулю (в противном случае (5) – алгебраическая поверхность первого порядка, т.е. плоскость).
В зависимости от значений коэффициентов возможны случаи, когда уравнение (5) определяет вырожденную поверхность (пустое множество,
точку, прямую, плоскость, пару плоскостей). |
|
|||
Например, уравнение x2 |
+ y2 |
+ z 2 |
+1 = 0 не имеет решений и задает пустое |
|
множество, уравнение x2 + y2 |
+ z 2 |
= 0 |
задает точку с координатами |
(0,0,0), |
уравнение x2 + y2 = 0 определяет прямую – координатную ось Oz , x2 = 0 |
задает |
|||
координатную плоскость x = 0 , уравнение x2 =1 задает пару плоскостей |
x = −1 |
|||
и x =1. |
|
|
|
|
Далее будем рассматривать только невырожденные поверхности. Поверхности второго порядка обладают определенными элементами
симметрии. Некоторые имеют центр симметрии; все имеют хотя бы одну
плоскость симметрии; многие имеют ось симметрии.
Всякое уравнение вида (5) посредством преобразования координат, т.е. сдвигов и поворотов (так называемое приведение к главным осям), можно привести к каноническому виду. В уравнении канонического вида каждая переменная содержится только в одной степени: либо только в нулевой, либо только в первой, либо только во второй. Канонический вид уравнение принимает, когда оси системы координат совпадают с осями симметрии поверхности, а начало системы координат выбрано специальным образом (для центрально-симметричных поверхностей совпадает с центром симметрии).
2. ИССЛЕДОВАНИЕ ФОРМЫ ПОВЕРХНОСТЕЙ ВТОРОГО ПОРЯДКА ПО ИХ КАНОНИЧЕСКИМ УРАВНЕНИЯМ
Основным методом исследования формы поверхности по ее уравнению является метод сечений, когда о форме поверхности судят по форме кривых, которые получаются при пересечении данной поверхности плоскостями
x = const; y = const; z = const.
67
Последовательно рассмотрим канонические уравнения поверхностей второго порядка.
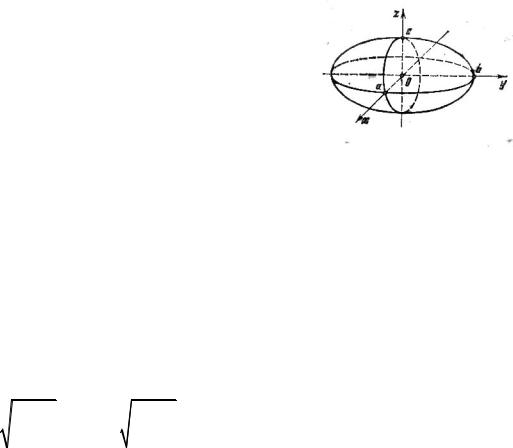
2.1. Эллипсоид
Эллипсоидом называется поверхность второго порядка с каноническим уравнением
|
x2 |
+ |
y2 |
+ |
z2 |
=1. |
|
|
a2 |
b2 |
c2 |
|
|||
|
|
|
|
|
|||
Рассмотрим |
|
|
сечение |
эллипсоида |
|||
плоскостью |
z = 0 . |
Линия |
пересечения |
||||
эллипсоида и плоскости задается системой уравнений
|
2 |
|
y |
2 |
|
z |
2 |
|
|
|
2 |
|
y |
2 |
|
||
|
x |
|
+ |
|
+ |
|
=1, |
или |
|
x |
|
+ |
|
=1, |
|||
|
|
b2 |
c2 |
|
|
b2 |
|||||||||||
a2 |
|
|
|
a2 |
|
|
|||||||||||
|
= 0, |
|
|
|
|
|
|
|
= 0. |
|
|
||||||
z |
|
|
|
|
|
|
z |
|
|
||||||||
Очевидно, что линия пересечения – эллипс с полуосями а и b. Рассмотрим сечение эллипсоида плоскостью z = h . Линия пересечения
задается системой уравнений
|
|
2 |
|
|
2 |
|
|
|
2 |
|
|
|
|
|
x2 |
y2 |
|||||
|
|
x |
|
+ |
y |
|
|
+ |
z |
|
|
=1, |
|
|
|
|
|
|
+ |
|
=1, |
|
|
|
|
|
|
или |
|
2 |
2 |
||||||||||||
|
|
|
b2 |
|
c2 |
||||||||||||||||
|
a2 |
|
|
|
|
a1 |
b1 |
||||||||||||||
|
|
= h, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
z |
|
|
|
|
|
|
|
|
|
|
z = h, |
|
|
|||||||
где a = a |
1− |
h2 |
; b = b |
1− |
h2 |
. Таким образом, если 0 < h < c , то сечение – |
|||||||||||||||
|
|
||||||||||||||||||||
1 |
|
|
|
c2 |
|
|
1 |
|
|
|
|
|
c2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
эллипс с полуосями a1 |
< a; b1 |
< b . Если h = c , сечение – точка с координатами |
|||||||||||||||||||
(0,0,c). Если h > c , |
система решений не имеет, т.е. исследуемая поверхность не |
||||||||||||||||||||
имеет общих точек с рассматриваемой плоскостью. |
|||||||||||||||||||||
Аналогично |
|
рассматриваются |
сечения поверхности S плоскостями |
||||||||||||||||||
x = const , |
y =const . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Величины a,b,c называются полуосями эллипсоида. Если все они
различны, эллипсоид называется трехосным. При равенстве двух полуосей получаются эллипсоиды вращения: при a =b < c - вытянутый, при a =b > c -
сплющенный. Эти поверхности получаются при вращении эллипса,
соответственно, вокруг большой и малой оси.
Если a = b = c = R , каноническое уравнение принимает вид x2 + y2 + z2 = R2
и задает сферу с центром в начале координат и радиусом R.
68