
- •ВВЕДЕНИЕ
- •1.1. Понятие моделирования
- •1.2. Виды моделирования
- •1.2.1. Физическое моделирование
- •1.2.2. Математическое моделирование
- •1.3. Классификация математических моделей
- •1.4. Понятие об адекватности математической модели
- •МОДЕЛИРОВАНИЯ
- •Рис.2.1. Блок-схема объекта моделирования
- •2.2. Пассивный эксперимент: общая характеристика
- •2.3. Понятие об уравнении регрессии
- •2.4. Построение линейной модели статики
- •Таблица 2.2
- •Рис.2.4. Блок-схема объекта (при n=1)
- •2.5. Регрессионный анализ результатов моделирования
- •Рис.2.6. Тональная аудиограмма при остром среднем отите
- •2.5.3. Проверка гипотезы об адекватности математической модели
- •2.6. Построение множественной линейной модели
- •2.8. Математические модели на основе активных экспериментов
- •3.2. Модели, характеризующие режим течения материального потока
- •4. ИМИТАЦИОННОЕ МОДЕЛИРОВАНИЕ БТС
- •4.1. Понятие об имитационном моделировании
- •4.2. Понятие о компартментной системе
- •5. ПРИМЕНЕНИЕ СИСТЕМЫ MATLAB
- •ДЛЯ РЕШЕНИЯ ЗАДАЧ МОДЕЛИРОВАНИЯ ЭЛЕМЕНТОВ БТС
- •ЗАКЛЮЧЕНИЕ
|
|
|
35 |
|
|
(р=5%) и уровне свободы f = N ( m −1 ) |
из таблицы (приложение 3) выби- |
||||
рают |
tb |
[6]. Если |
|
|
|
|
таб |
|
|
|
|
|
|
tb |
> tb |
, |
(2.26) |
|
|
i |
таб |
|
|
то bi – не случайно, а значимо отличен от нуля.
Если tbi ≤tbтаб , то bi – случайно отличен от нуля, это незначимый коэффициент, который исключается из уравнения ( bi = 0 ).
Так как все члены уравнения взаимно коррелированны, удаление одного из них приводит к необходимости пересчитать заново значения оставшихся. В уравнении математической модели должны остаться только значимые коэффициенты.
В знаменателе формулы (2.25) используют оценку среднего квадратического отклонения соответствующего коэффициента регрессии:
j=N |
∂b |
2 |
(2.27) |
Sbi = ∑j=1 ( |
i |
)S j . |
|
∂y j |
|
Для линейного уравнения вида (2.11) можно определить Sb0 ,Sb1 по более простым формулам:
|
|
i=N |
|
||
Sb |
= |
Sвоспр2 ∑x12i |
; |
||
i=1 |
|||||
i=N |
i=N |
||||
0 |
|
|
|||
|
|
N ∑x12i −(∑x1i )2 |
(2.28) |
||
|
|
i=1 |
i=1 |
||
Sb |
= |
Sвоспр2 |
N |
. |
|
i=N |
i=N |
||||
1 |
|
|
|||
|
|
N ∑x12i −(∑x1i )2 |
|
||
|
|
i=1 |
i=1 |
|
|
2.5.3. Проверка гипотезы об адекватности математической модели
Наиболее распространенной метрикой для оценки расстояния между экспериментальными значениями y и значениями, найденными по уравне-
36
нию модели ( y ) является формула остаточной дисперсии. Если при постановке эксперимента были выполнены параллельные измерения Y, остаточную дисперсию находят как
|
m |
i=N |
(2.29) |
|
Sост2 = |
∑( yi − y)i )2 , |
f1 = Nm −(n +1). |
||
|
||||
|
f1 i=1 |
|
||
Проверку адекватности математической модели осуществляют с помощью критерия Фишера:
|
2 |
|
(2.30) |
Fрас = |
Sост |
. |
|
|
|
||
|
Sвоспр2 |
|
|
Уравнение математической модели адекватно исследуемому объекту, если
Fрасч < Fтаб, p, f1 , f2 , |
при f1 = Nm − (n + 1), f2 = N (m − 1). |
(2.31) |
|
Если условие (2.31) не выполняется при Fтаб (приложение 2), модель
не адекватна. Такой результат может объясняться неудачно выбранным видом уравнения или влиянием на выходной параметр еще одного фактора, не учтенного в модели.
Формулы (2.29) – (2.31) можно использовать, если m>1.
Если параллельных замеров не проводилось (при m=1), дисперсию воспроизводимости определить нельзя. Тогда вместо проверки адекватности производится оценка качества аппроксимации опытных точек принятым уравнением регрессии. Остаточную дисперсию находят по формуле
|
1 |
i=N |
|
Sост2 = |
∑( yi − y)i )2 . |
||
f2 |
|||
|
i=1 |
Критерий Фишера оценивается по формуле
|
S 2 |
|
|
Fрас = |
y |
, |
|
Sост2 |
|||
|
|
где Sy2 – оценка дисперсии y относительно среднего (2.5).
(2.32)
(2.33)
Уравнение регрессии обеспечивает удовлетворительную точность аппроксимации, если
Fрасч |
> Fтаб,P, f , f |
(2.34) |
|
1 |
2 |
и f1 = N −1, f2 = N −n −1.
Если условие (2.34) не выполняется, модель не адекватна.
37
2.6. Построение множественной линейной модели
Предположим, имеется некоторый объект (рис.2.2), эффективность и качество его функционирования характеризует выходной параметр y. На него оказывают влияние некоторое множество внешних входных воздействий (факторов). Они образуют вектор входных координат объекта X_.
Если на множестве X_ выделить только линейно независимые координаты, т.е. сформировать множество X ={x1 , x2 ,...xn}, то, в случае ли-
нейной взаимосвязи между выходом объекта y и факторами, ее можно описать уравнением множественной линейной регрессии:
y) = b0 +b1 x1 +b2 x2 +... +bn xn , |
(2.35) |
Для выделения X осуществляется поиск на множестве X_ всех пар линейно зависимых факторов. Из каждой такой пары в множество X включается только один фактор. Последовательно анализируя составляющие X_, получим искомое множество линейно независимых факторов X X_.
На основе пассивного эксперимента можно сформировать экспериментальную выборку (табл.2.5).
Учитывая, что отдельные факторы могут представлять собой различные физические характеристики, для их объединения в одном уравнении необходимо перейти к единому, стандартизованному масштабу.
|
|
Таблица 2.5. |
|
|
|
|
|
N |
Факторы |
Параллельные замеры Y |
|
|
x1 |
x2 |
….. |
xn y1 |
…… |
ym |
|||
1 |
x11 |
x21 |
|
xn1 |
|
|
|||
2 |
x12 |
x22 |
|
xn2 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
N |
x |
1N |
x |
2N |
|
x |
nN |
|
|
|
|
|
|
|
|
|
|||
Стандартизация переменных выполняется с использованием следующих выражений:
|
y |
|
− y |
|
|
|
|
(2.36) |
|
y0 = |
i |
|
x |
0 |
= |
x ji − x j |
|||
|
|
, |
ji |
|
, j=1,..n; i=1, N, |
||||
|
S y |
|
|||||||
i |
|
|
|
|
|||||
|
|
|
|
|
|
Sx j |
|||
38
где Sy и Sx j – оценки средних квадратических отклонений соответ-
ствующих переменных, которые определяются по формулам, аналогичным формуле (2.6).
Экспериментальная выборка (табл.2.5), преобразованная с помощью (2.36), будет обладать новыми свойствами:
y |
0 |
= 0, S y0 =1 |
0 |
= 0 , |
Sx0j |
= 1 . |
(2.37) |
|
, x j |
|
С помощью стандартизованных переменных можно получить уравнение модели вида
y)0 = a1 x10 +a2 x20 +a3 x30 ... +an xn0 . |
(2.38) |
Коэффициенты уравнения (2.38) определяются из условия минимума функционала S:
i=N |
|
|
|
|
|
|
(2.39) |
|
S = ∑( yi0 − y)i0 )2 min; |
|
|
|
|||||
i=1 |
∂S |
|
∂S |
|
∂S |
|
(2.40) |
|
S min, если |
= 0, |
= 0, ... |
= 0. |
|||||
|
|
|
|
|||||
|
∂a1 |
∂a2 |
∂an |
|
||||
Используя совместно (2.38)-(2.40), получим систему нормализованных уравнений:
i=N |
|
i=N |
|
i=N |
|
(2.41) |
||||
a1 ∑(x10i )2 |
+ a2 ∑x10i x20i +...... =∑x10i yi0 ; |
|
|
|||||||
i=1 |
|
i |
=1 |
|
|
i=1 |
|
|
||
i=N |
|
i=N |
|
i=N |
|
|
||||
a1 ∑x20i x10i |
+a2 |
∑(x20i )2 +....... = ∑x20i yi0 ; |
|
|
||||||
i=1 |
|
i=1 |
|
i=1 |
|
|
||||
i=N |
|
i=N |
|
i=N |
|
|
||||
a1 ∑xni0 x10i |
+a2 |
∑xni0 x20i |
+....... = |
∑xni0 yi0 . |
|
|
||||
i=1 |
|
i=1 |
|
i=1 |
|
|
||||
Умножим левую и правую части уравнения (2.39) на |
1 |
и введем |
||||||||
N-1 |
||||||||||
обозначения |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
(2.42) |
||
|
|
|
1 |
|
N |
|
|
|||
r*0 0 |
= |
|
xij0 xik0 . |
|
|
|
||||
|
|
|
|
|
|
|||||
|
x j xk |
|
|
N −1 ∑i=1 |
|
|
|
|||
Вместо (2.41) получим систему нормализованных уравнений вида

|
|
|
|
|
|
|
39 |
|
|
|
|
|
* |
|
|
* |
+ |
|
* |
; |
|
|
(2.43) |
a1 +a2 rx10 x20 |
+a3rx10 x30 |
...... = ry0 x10 |
|
|
|
||||||
...... |
|
|
|
|
|
|
|
|
|
|
|
a r*0 0 |
+a |
r*0 0 |
+a r*0 |
0 |
+...... +a |
n |
= r*0 |
0 . |
|||
1 xn xn |
|
2 |
xn x2 |
3 |
xn x3 |
|
|
y |
x1 |
||
Решая систему алгебраических уравнений (2.43), определим коэффициенты уравнения (2.38). Для перехода к уравнению (2.35) используют выражения
|
Sy |
|
n |
(2.44) |
bj = a j |
, |
b0 = y −∑bj x j . |
|
|
|
|
|||
|
Sx j |
j=1 |
|
|
Для уравнения (2.35) можно определить коэффициент множественной корреляции R:
R = |
a1ryx1 + a2 ryx2 +...an ryxn , 0 ≤ R ≤1. |
(2.45) |
|
Коэффициент множественной корреляции служит показателем силы связи в случае множественной регрессии.
В ходе регрессионного анализа проверяются гипотезы об однородности дисперсий параллельных измерений Y, о значимости оценок коэффициентов регрессии и об адекватности уравнения математической модели.
Следует учитывать, что все коэффициенты уравнения регрессии, построенного на основе результатов пассивного эксперимента, взаимосвязаны, и для проверки значимости коэффициентов целесообразно применять итерационную процедуру.
На каждой итерации определяются расчетные значения t-критерия для всех коэффициентов в уравнении модели. Найденные значения
{tb |
,tb |
,tb ....tbn } упорядочиваются по убыванию. Из уравнения исключа- |
1 |
2 |
3 |
ется коэффициент bi , для которого получен наименьший t-критерий ( tbi ).
Оставшиеся оценки коэффициентов регрессии b1,b2 ,...bi−1,bi+1,...bn пе-
ресчитываются. Процедура повторяется до тех пор, пока наблюдается снижение остаточной дисперсии.
Задачу построения линейной математической модели вида (2.35) можно решать с помощью программ, имеющих средства вычисления статистических функций. Это специальные пакеты: Statgraphics+ for Windows, Statistica, MatLab и т.п., или более широко применяемая программа MS Excel. Программы из пакета Microsoft Office имеют простые и легко настраиваемые графические средства, а программа Excel очень удобна при обработке двумерных массивов, с помощью которых обычно задаются результаты пассивного эксперимента.

40
Рассмотрим процедуру построения линейной математической модели с помощью библиотеки статистических функций программы MS Excel.
Пусть результаты пассивного эксперимента представляются в виде первых пяти столбцов таблицы 2.6.
Предположим, что на выходной параметр оказывают влияние все указанные в таблице факторы. Тогда, используя массив экспериментальных данных в качестве аргументов функции ЛИНЕЙН(..), можно получить оценки коэффициентов уравнения линейной модели.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 2.6. |
||
|
I |
|
x |
|
x |
2 |
|
x3 |
|
yi |
|
y)1i |
|
y)2i |
|
y)3i |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
2 |
|
3 |
|
|
4 |
|
5 |
|
6 |
|
7 |
|
8 |
|
|
|
1 |
|
0,4 |
|
2,6 |
|
|
0,06 |
|
34,00 |
|
33,99861 |
|
34,004 |
|
40,1538 |
|
|
|
2 |
|
1,6 |
|
2,8 |
|
|
0,8 |
|
48,81 |
|
48,8063 |
|
48,80398 |
|
55,62965 |
|
|
|
3 |
|
2,4 |
|
3,6 |
|
|
0,092 |
|
60,00 |
|
59,99886 |
|
60,00517 |
|
65,94689 |
|
|
|
4 |
|
3,2 |
|
6 |
|
|
0,24 |
|
74,40 |
|
74,40062 |
|
74,40922 |
|
76,26412 |
|
|
|
5 |
|
0,8 |
|
4 |
|
|
0,36 |
|
41,60 |
|
41,60189 |
|
41,60638 |
|
45,31242 |
|
|
|
6 |
|
3,6 |
|
9,4 |
|
|
2,2 |
|
86,02 |
|
86,02161 |
|
86,01519 |
|
81,42274 |
|
|
|
7 |
|
0,48 |
|
0,4 |
|
|
0,4 |
|
30,56 |
|
30,56192 |
|
30,56003 |
|
41,18553 |
|
|
|
8 |
|
0,68 |
|
11,2 |
|
1 |
|
54,57 |
|
54,56948 |
|
54,57933 |
|
43,76483 |
|
|
|
|
9 |
|
0,56 |
|
6,24 |
|
1,4 |
|
43,21 |
|
43,21312 |
|
43,21047 |
|
42,21725 |
|
|
|
|
10 |
|
0,84 |
|
12,24 |
|
1,8 |
|
58,58 |
|
58,57801 |
|
58,58114 |
|
45,82828 |
|
|
|
|
11 |
|
1,08 |
|
8,7 |
|
|
2,2 |
|
54,38 |
|
54,38178 |
|
54,37472 |
|
48,92345 |
|
|
|
12 |
|
1,2 |
|
6,28 |
|
2,8 |
|
50,99 |
|
50,9878 |
|
50,97035 |
|
50,47104 |
|
|
|
На рис.2.7а приведен фрагмент массива с результатами, на основе которых уравнение модели имеет вид
y)1 = 23.99 +11.99x1 +2x2 +0.01x3 . |
(2.46) |
Результаты выполнения функции ЛИНЕЙН (строки с номерами 1 – 5) дополнены (строка с номером 0) расчетными значениями критерия Стью-
дента (2.25):
tb0 = |
|
b0 |
|
= |
23.99977 |
= 14477.39 |
при i = 0,1,2,3. |
|
|
|
|
||||
Sb |
0.001657 |
||||||
|
|
0 i |
|
|
|
|
|
В пятой строке приведены суммарные оценки отклонений расчетного значения выходного параметра от экспериментального:
i=N |
i=N |
SS _ reg = ∑( y − y)1i )2 , |
SS _ ost = ∑( yi − y)1i )2 . |
i=1 |
i=1 |
В соответствии с полученными значениями критерия Стьюдента из уравнения (2.46) надо исключить x3 , т.к. велика вероятность, что коэффи-
циент b3 случайно отличен от нуля. При повторном использовании функ-

41
ции ЛИНЕЙН( ) с экспериментальным массивом y и факторами x1 и x2 получим (рис.2.7б) уравнение, отличающееся от предыдущего варианта только в третьем, четвертом знаках после запятой:
(а) |
|
y)1 = 23.99 +11.99 x1 +2x2 . |
|
|
(2.47) |
||||||
|
|
|
|
|
|
|
|
|
|
||
|
t_bi |
1 |
2 |
|
3 |
|
4 |
|
5 |
|
|
|
10,530 |
7688,25 |
|
17296,6 |
|
14477,39 |
|
0 |
|
||
|
bi |
0,0105 |
2,0 |
|
11,9 |
|
23,9 |
|
1 |
|
|
|
S_bi |
0,00099 |
0,00026 |
|
0,00069 |
|
0,00165 |
|
2 |
|
|
|
|
0,99 |
<= r |
|
|
|
|
3 |
|
||
|
|
|
f2 => |
8 |
|
|
|
|
|
4 |
|
|
|
2744,6 |
4,92E-05 |
|
|
|
|
5 |
|
||
(б) |
|
SS_reg |
SS_ost |
|
|
|
|
6 |
|
||
|
|
|
|
|
|
4 |
|
|
|
||
|
|
|
1 |
2 |
|
3 |
|
|
5 |
|
|
|
t_bi |
|
|
2676,48 |
|
4760,9 |
|
4003,74 |
|
0 |
|
|
bi |
|
|
2,0017 |
|
11,9 |
|
23,99 |
|
1 |
|
|
S_bi |
|
|
0,000748 |
|
0,0025 |
|
0,0059 |
|
2 |
|
|
|
|
0,999 |
<= r |
|
|
|
|
|
3 |
|
|
|
|
f2 => |
9 |
|
|
|
|
|
4 |
|
|
|
|
2744,63 |
0,00073 |
|
|
|
|
|
5 |
|
|
|
|
SS_reg |
SS_ost |
|
|
|
|
|
6 |
|
(в)
t_bi |
1 |
|
2 |
3 |
4 |
5 |
|
|
|
6,09 |
9,47 |
0 |
|
bi |
|
|
|
12,89 |
34,99 |
1 |
S_bi |
|
|
|
2,11 |
3,69 |
2 |
|
0,788 |
|
<= r |
|
|
3 |
|
f2 => |
|
10 |
|
|
4 |
|
2163,2 |
|
581,42 |
|
|
5 |
|
SS_reg |
SS_ost |
|
|
6 |
|
Рис. 2.7. Фрагменты результатов оценки коэффициентов уравнения множественной линейной регрессии с помощью функций Excel: а – для уравнения (2.46), б – для уравнения (2.47), в – для уравнения (2.48)
Но так как из (2.47) исключен третий фактор, сумма остатков, характеризующая разброс экспериментальных точек относительно уравнения модели, выросла почти в 14 раз. Однако коэффициент r изменился слабо и условие адекватности (2.34) для (2.47) выполняется.
42
Если из уравнения модели исключить x2 , полученные результаты (рис.2.7в) покажут существенный рост суммарных остатков и резкое снижение коэффициента r
y)1 = 34.995 +12.89 x1 |
(2.48) |
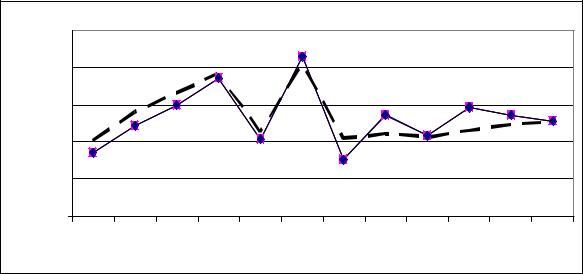
Расчет с помощью функции ТЕНДЕНЦИЯ(..) оценок выходного параметра (столбцы 6-8 в табл.2.6) для уравнений (2.46) – (2.48) позволяет построить графики их изменения (рис.2.8).
100,00 |
|
|
|
|
|
|
|
|
|
|
|
80,00 |
|
|
|
|
|
|
|
|
|
|
|
60,00 |
|
|
|
|
|
|
|
|
|
|
|
40,00 |
|
|
|
|
|
|
|
|
|
|
|
20,00 |
|
|
|
|
|
|
|
|
|
|
|
0,00 |
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
Рис. 2.8. Диаграмма изменения оценок выходного параметра по уравнениям (2.46), |
|||||||||||
(2.47) – сплошная линия, по уравнению (2.48) – пунктирная линия |
|
|
|
||||||||
Для рассматриваемого примера в качестве математической модели целесообразно использовать уравнение (2.47).
Аналогичный вывод можно получить с помощью программы Statgraphics+ for Windows.
Для построения линейной модели в ней используется команда Multiple Regression. В программе предусмотрен автоматический расчет критериев Стьюдента и генерации рекомендаций по исключению не значимых коэффициентов из уравнения.
Протокол решения этого примера приведен на рис.2.9.

43
(а)
Multiple Regression Analysis
--------------------------------------------------------------------------------------------------
Dependent variable Col_4 |
|
Standard |
|
|
|
Parameter |
Estimate |
Error |
CONSTANT |
24,0 |
0,0 |
Col_1 |
12,0 |
0,0 |
Col_2 |
2,0 |
0,0 |
Col_3 |
0,01 |
0,0 |
|
|
Analysis of Variance |
|
Source |
Sum of Squares |
Df |
Mean Square |
Model |
2744,53 |
3 |
914,842 |
Residual |
0,0 |
8 |
0,0 |
The StatAdvisor
---------------------
The output shows the results of fitting a multiple linear regression model to describe the relationship between Col_4 and 3 independent variables. The equation of the fitted model is
Col_4 = 24,0 + 12,0*Col_1 + 2.0*Col_2 + 0,01*Col_3
(б)
Multiple Regression Analysis
--------------------------------------------------------------------------------------------------
Dependent variable Col_4
|
|
Standard |
T |
|
Parameter |
Estimate |
Error |
Statistic |
|
CONSTANT |
|
0,00550003 |
|
|
24,0017 |
4363,92 |
|
||
Col_1 |
bi 11,99980 |
0,000231264 |
5188,79 |
tb |
|
|
|
|
i |
Col_2 |
2,00159 |
0,000686254 |
2916,69 |
|
|
Analysis of Variance |
|
|
|
Source |
Sum of Squares |
Df |
Mean Square |
|
Model SS_reg |
2744,53 |
2 |
1372,262 |
|
Residual |
0,000614987 |
9 |
0,00006833 |
|
Total (Corr. ) |
2744,53 |
11 |
|
|
The StatAdvisor |
The equation of the fitted model is |
|
|
|
Col_4 = 24,0017 + 11,9998*Col_1 + 2,00159*Col_2 |
|
|
||
y |
x1 |
x2 |
|
|
Рис. 2.9. Фрагменты протокола оценки коэффициентов уравнения множественной линейной регрессии с помощью функций Statgraphics+ for Windows. (а) – для уравнения
(2.46), (б) – для уравнения (2.47)
44
2.7. Построение нелинейных моделей, описывающих статический режим работы объекта
Предположим, что функциональная связь между выходным параметром и факторами является нелинейной. В зависимости от вида нелинейной функции возможны различные методики построения уравнений математической модели. Рассмотрим несколько примеров построения нелинейных моделей статики.
Рассмотрим первый пример. Если для описания взаимосвязи между Y и X можно использовать нелинейный полином некоторой степени, то для определения коэффициентов уравнения модели используют метод наименьших квадратов.
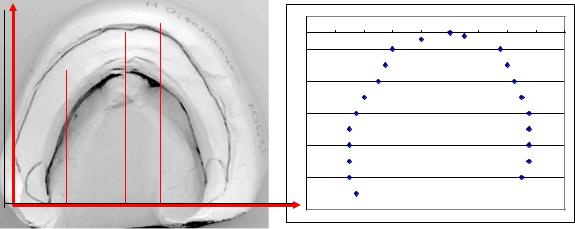
В качестве объекта исследования рассмотрим гипсовый слепок нижней челюсти человека (рис.2.10). Привязка проекции оттиска на плоскость YOX позволяет получить набор точек, задающих внешний (или внутрен-
ний) профиль челюсти. Полученную выборку координат точек { ( yi , xi ) } |
||||||||||
можно рассматривать как совокупность значений фактора ( x1 ) и выходно- |
||||||||||
го параметра (y). Выдвинута гипотеза о том, что внешний профиль челю- |
||||||||||
сти можно описать с помощью уравнения параболы второго порядка |
||||||||||
(2.46). |
|
|
|
|
|
|
|
|
|
|
-5 |
0 |
10 |
20 |
30 |
40 |
50 |
60 |
70 |
80 |
90 |
Y |
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
15 |
|
|
|
|
|
|
|
|
|
|
25 |
|
|
|
|
|
|
|
|
|
|
35 |
|
|
|
|
|
|
|
|
|
|
45 |
|
|
|
|
|
|
|
|
|
|
X 55 |
|
|
|
|
|
|
|
|
|
|
Рис. 2.10. Привязка системы координат Рис. 2.11. Внешний профиль челюсти |
|
|||||||||
к сканированному изображению гип- |
|
|
|
|
|
|
|
|
|
|
сового слепка нижней челюсти чело- |
|
|
|
|
|
|
|
|
|
|
века |
|
|
|
|
|
|
|
|
|
|
yˆ = b0 +b1x1 + b11x12. |
|
|
|
|
|
|
(2.46) |
|||
Следует найти такие значения коэффициентов b0, b1, |
b11, |
|
которые |
|||||||
обеспечат минимум функционала: |
|
|
|
|
|
|
|
|
|
|
N
ф= ∑( yi − y)i )2 → min
i=1
45 |
|
N |
(2.47) |
илиф= ∑( yi −b0 |
−b1 x1 −b11 x12 )2 . |
i=1 |
|
Минимум функционала достигается при выполнении требований:
∂Ф = 0; |
∂Ф = 0; |
∂Ф = 0. |
(2.48) |
|
|
|
|
|
|
∂b |
∂b |
|
|
|
∂b |
|
|
||
0 |
1 |
11 |
|
|
Выражения (2.48) с учетом (2.47) позволяют получить систему нор-
мальных уравнений: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∑yu ; |
(2.49) |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|||||||
|
b0 N +b1 ∑xi +b11 ∑xi = |
|
|||||||||||||||||||||
|
|
∑ |
2 |
|
|
∑ |
2 |
|
|
∑ |
xi3 = |
∑ |
|
|
|
|
|||||||
|
|
+b1 |
xi |
3 |
+ b11 |
xi yu ; |
|
||||||||||||||||
b0 |
|
|
xi |
∑ |
|
|
∑ |
|
|
|
|||||||||||||
|
∑ |
|
|
|
|
|
|
|
|
|
xi4 = |
∑ |
xi2 yu . |
|
|||||||||
b0 |
|
|
xi |
+b1 |
|
|
xi |
|
+ b11 |
|
|
|
|
|
|
||||||||
Решая систему алгебраических уравнений (2.49), получим |
|
||||||||||||||||||||||
|
|
|
|
b = |
D0 |
, |
b = |
D1 |
, |
b |
= |
D2 |
, |
(2.50) |
|||||||||
|
|
|
|
0 |
|
D |
|
1 |
|
D |
|
|
11 |
|
|
D |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
где D – главный определитель системы, D0 ,D1 ,D2 – алгебраиче- |
|||||||||||||||||||||||
ские дополнения. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2.51) |
|
|
|
|
|
|
|
|
|
|
|
|
N |
|
|
|
N |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
N |
|
∑x1i |
∑x12i |
|
|
|
|
||||||||
|
|
|
|
|
|
|
N |
|
|
i=1 |
|
|
|
i=1 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
N |
|
|
|
N |
|
|
|
|
|
|
|||
|
|
|
|
D = |
∑x1i |
|
∑x12i |
∑x13i |
|
. |
|
||||||||||||
|
|
|
|
|
|
|
i=1 |
|
|
i=1 |
|
|
|
i=1 |
|
|
|
|
|||||
|
|
|
|
|
|
|
N |
|
|
|
N |
|
|
|
N |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
∑x12i |
|
∑x13i |
∑x14i |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
i=1 |
|
|
i=1 |
|
|
|
i=1 |
|
|
|
|
|
|
|||
Аналогичным образом определяют выражения для расчета оценок коэффициентов регрессии любого полиномиального уравнения.
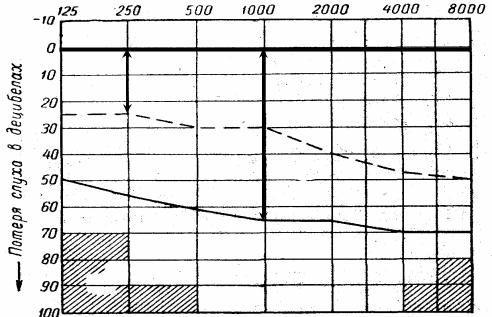
Традиционная графическая форма представления тональной пороговой аудиограммы является отображением значений порогов слышимости звука на отдельных частотах, измеренных по воздушному и костному проведениям (рис.2.12). По оси абсцисс в логарифмическом масштабе откладывают значения частот fi (fi {125, 250, ..., 16000}, Гц), на которых проводят
исследования, по оси ординат - потери слуха Yi (Yi = −15 ,..., 110 , дБ;
Y=5 дБ). Нулевой линией отмечены средние потери слуха, измеренные у хорошо слышащих людей [8, 9]. При наличии патологий органов слуха на аудиограмме фиксируется увеличение потерь слуха на отдельных частотах.
46
Например, на рисунке 2.12 точка П1 характеризует потери слуха по костному проведению на частоте 250 Гц; точка П2 – потери слуха по воздушному проведению на частоте 1000 Гц.
Известно, что аудиограммы одного и того же пациента, снятые с некоторым временным сдвигом в течение одного дня (или нескольких дней), будут различаться [10]. Учитывая эти объективные наблюдения, рассмотрим возможность построения формализованного описания кривых потерь слуха с целью создания модели порогов слуха. Вполне очевидно, что в качестве зависимой переменной y надо рассматривать потери слуха.
Так как речь идет об аппроксимации плоских кривых, то число независимых переменных не должно превышать n ≤ 1. Единственной независимой переменной x является частота испытательного сигнала.
Нулевая ли-
ПП
Рис.2.12. Тональная пороговая аудиограмма при наличии патологии слуха
Так как ее значения Х, определяющие область изменений фактора x, всегда постоянны (Х=125, 250 и т.д.), то для упрощения модели будем использовать в качестве Х порядковый номер частоты испытательного сигнала. Тогда фактор (x) будет принимать значения на множестве 1, 2, 11.
Учитывая отмеченные в литературе возможные формы кривых порогов слуха [10], для построения уравнения модели используем полиномиальное уравнение вида
|
m =6 |
|
y) |
= ∑ bi x i , m – порядок полинома. |
(2.52) |
i =0

47
Для оценки коэффициентов уравнения (2.52) используем выборку из нескольких аудиометрических кривых, полученных по воздушному проведению при исследовании слуха одного пациента (рис. 2.13, 2.14). Исследования проводились с помощью автоматизированного компьютерного аудиометра [12].
Рис.2.13. Фрагмент выборки аудиометрических кривых, полученных по воздушному |
||
проведению при исследовании слуха пациента N 1 |
|
|
Каждый эксперимент представлен одной строкой, в последнем столбце |
||
приведены оценки дисперсии потерь слуха, в последней строке приведены |
||
средние значения потерь слуха на каждой частоте. |
|
|
100 |
1000 |
10000 |
0 |
|
|
10 |
|
|
20 |
|
|
30 |
|
|
40 |
|
|
50 |
|
|
60 |
|
|
70 |
|
|
Рис.2.14. Кривые порогов слышимости по воздушному проведению пациента N1 |
||
Анализ кривых порогов слышимости на рис.2.14 показывает, что для построения аппроксимирующего уравнения необходимо использовать полином не ниже второго порядка.
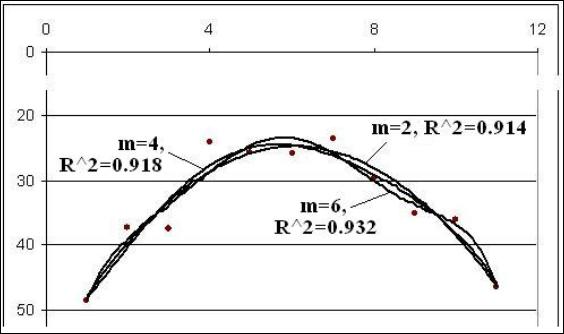
На рис. 2.15 показаны варианты аппроксимации средних порогов слышимости уравнением (2.52) при m≥2.
48
Рис.2.15. Аппроксимация средних порогов слышимости полиномиальными уравнениями
Из сравнения оценок показателя достоверности аппроксимации (R^2) следует, что для формализованного описания кривых порогов слуха рассматриваемого пациента достаточно уравнения второго порядка m=2:
y) = 0.89 x 2 −10 .83 x1 + 57 .65 x 0 |
(2.53) |
Для проверки адекватности модели необходимо располагать оценками остаточной дисперсии ( Sост2 ) и критерия Фишера ( Fрас ):
|
Sy2 |
2 |
1 |
i=N |
) |
2 |
|
|
|
|
|
Fрас = |
|
, |
Sост = |
|
∑(yi − yi ) |
|
, |
f1 |
= N −1, f2 |
= N − n −1, (2.54 |
|
2 |
f2 |
|
|||||||||
|
Sост |
|
i=1 |
|
|
|
|||||
где Sy2 – дисперсия выходного параметра относительно среднего, n=1. Условие адекватности:
Fрасч > Fтаб,P, f , f |
p = 5% |
(2.55) |
1 |
2 |
|
Если условие (2.55) выполняется, исследуемое уравнение обеспечивает удовлетворительную точность аппроксимации.
На рис. 2.16 приведены оценки коэффициентов уравнений аппроксимирующих пороги слышимости из выборки пациента 1 и значения критерия Фишера.
49
Сравнение результатов с табличным значением F критерия (при 5%- ном уровне статистической значимости) показывает, что только в 5-м эксперименте гипотеза об адекватности уравнений 2-го порядка не подтвер-
ждается. Анализируя оценки коэффициентов b0 , b1 , b11 в разных урав-
нениях, можно утверждать, что они изменяются слабо, отклонения составляют от 3 до 8%.
N экспер |
1 |
2 |
3 |
4 |
5 |
ПС_средн |
b11 |
1,1072 |
0,9848 |
1,0781 |
0,9848 |
0,7226 |
1,0388 |
b1 |
-12,287 |
-10,682 |
-11,528 |
-10,955 |
-7,6713 |
-11,363 |
b0 |
58,242 |
54,242 |
53,667 |
53,152 |
35,061 |
54,826 |
F_ras |
10,3322 |
18,98429 |
15,43574 |
6,245065 |
2,519202 |
13,9710165 |
F_tab |
3,19 |
3,19 |
3,19 |
3,19 |
3,19 |
3,19 |
Рис.2.16. Коэффициенты уравнений вида (2.52) при аппроксимации кривых порогов слышимости, приведенных на рис.2.15
Исследование модели порогов слуха показало, что, несмотря на довольно значительные отклонения оценок потерь слуха на отдельных частотах от аппроксимирующего уравнения, общий характер их изменения при переборе частот сохраняется. Из этого результата сделан следующий вывод. Форма кривых порогов слышимости является наиболее устойчивым признаком, который мало зависит от точности регистрации потерь слуха на отдельных частотах.
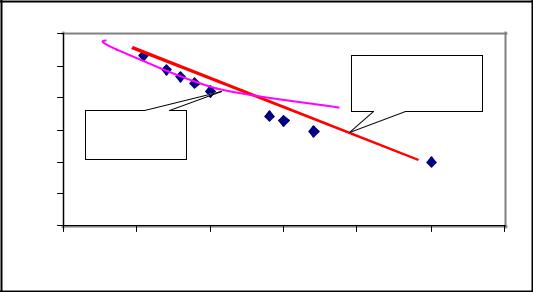
Рассмотрим второй пример. Предположим, что выходной параметр зависит только от одного фактора. Для определения вида уравнения математической модели, описывающей влияние фактора на выходной параметр, воспользуемся графиком в координатах Y-X, построенным по экспериментальным данным (рис.2.17). Для приведенного варианта распределения экспериментальных точек визуально подходят для аппроксимации как линейная функция, так и слабо выраженная нелинейная зависимость.
Предположим, что на первом этапе исследования объекта сделана попытка создать линейную модель вида yˆ = b0 +b1x1 . В ходе регрессионного
анализа выяснено, что это уравнение не обеспечивает удовлетворительную точность аппроксимации экспериментальных данных. На втором этапе ис-
следовалось уравнение параболы второго порядка y) = b0 +b1x1 +b22 x12 . Это
уравнение также не обеспечивает удовлетворительную точность аппроксимации экспериментальных данных, кроме того, величина остаточной дисперсии для этого уравнения увеличилась по сравнению с линейной моделью.
|
|
|
50 |
|
|
|
1,20Y |
|
|
|
|
|
|
1,00 |
|
|
|
|
yˆ = b0 +b1 x1 |
|
0,80 |
|
|
|
|
|
|
0,60 |
y=f (x,xk ) |
|
|
|
|
|
0,40 |
|
|
|
|
X |
|
0,20 |
|
|
|
|
|
|
|
|
|
|
|
|
|
0,00 |
|
|
|
|
|
|
0 |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,6 |
|
Рис. 2.17. Аппроксимация нелинейной зависимости |
|
||||
Рассмотренный пример иллюстрирует рост остаточной дисперсии при увеличении порядка полинома на фоне экспериментальной выборки малых объёмов. В этом случае лучшие результаты достигаются при использовании для аппроксимации экспериментальных данных трансцендентных выражений.
Например, для аппроксимации экспериментальных данных на рис.2.17 можно использовать экспоненциальную функцию вида
yˆ = S Rx1 . |
(2.56) |
Для определения оценок коэффициентов S и R необходимо выполнить линеаризацию исходного уравнения модели (2.56). С этой целью прологарифмируем правую и левую части уравнения:
lg yˆ = lg S + x1 lg R. |
(2.57) |
Введем обозначения:
lg yˆ = Z, lg S = b0 , lg R = b1, x1 = t1 . |
(2.58) |
Тогда вместо (2.52) получим линейное уравнение
Z = b0 +b1t1. |
(2.59) |
Оценки b0 и b1 находим методом наименьших квадратов по формулам (2.17), используя вместо y новую переменную Z, а вместо фактора х1 - новую переменную t1.
Для этого необходимо предварительно создать выборку Z и t1 .
Если экспериментальные данные заданы табл. 2.7, то, применяя к ним формулы (2.58), сформируем табл. 2.8.
51
Таблица 2.7
i |
x1 |
|
|
Y |
|
|
y1 |
y2 |
… |
ym |
|||
|
|
|||||
1 |
x11 |
y11 |
… |
… |
… |
|
2 |
x12 |
y12 |
… |
|
|
|
. |
|
|
|
|
|
|
. |
|
|
|
|
|
|
. |
|
|
|
|
|
|
N |
x1N |
… |
|
|
… |
Таблица 2.8
i |
t1=x1 |
|
Z=lg(y) |
|
||
Z1 |
Z2 |
… |
Zm |
|||
|
|
|||||
1 |
t11 |
lg y11 |
… |
… |
… |
|
2 |
t12 |
lg y12 |
… |
|
… |
|
. |
|
… |
|
|
|
|
. |
|
|
|
|
||
. |
t1N |
|
|
|
… |
|
N |
|
|
|
|||
Используя данные из таблицы 2.8, найдем b0 и b1 . Проверим адекват-
ность (или точность аппроксимации) линеаризованного уравнения (2.59). Выполним переход к исходному уравнению модели:
S = 10b0 , R = 10b1 |
(2.60) |
Проверим гипотезу об адекватности уравнения (2.56), используя данные из таблицы 2.7 и найденные значения коэффициентов (2.60).
Рассмотрим третий пример. Если на выходной параметр оказывают
влияние более одного фактора ( n > 1), порядок нелинейного полинома неизвестен и характер нелинейности на основе качественного анализа результатов экспериментов определить затруднительно, рекомендуется использовать для аппроксимации выражение вида
yˆ |
= R f1 (x1 ) f2 (x2 ) ... fn (xn ), |
(2.61) |
где R = const , |
fi (xi ) – вспомогательные функции одного аргумента. |
|
Эта методика дает хорошие результаты при исследовании объектов, для которых можно все факторы упорядочить по степени влияния на выходной параметр. Причем фактор, оказывающий наибольшее влияние на
Y, получает номер 1 ( x1 ), а фактор, меньше всего влияющий на выходной
параметр, – последний номер ( xn ).
Метод Брандона, использующий для построения нелинейной математической модели уравнение вида (2.61), основан на последовательном исключении из уравнения его членов.
Алгоритм метода включает следующие действия.
Исключается R : |
|
yi |
|
(2.62) |
|
yi0 |
= |
, |
|||
i = 1,2,...N; |
|||||
R |
|||||
|
|
|
|
||
и строится график |
y0 |
= f1 (x1 ), (рис. 2.18). |
|||

52
Рис. 2.18. График зависимости y0 (x1 ), определяемой по экспериментальным точкам
Выбирают функцию для аппроксимации точек на первом вспомогательном графике (например, для точек на рис. 2.18 можно использовать
уравнение прямой): |
|
|
f1 (x1 )= b01 +b11 x1. |
|
(2.63) |
|||||
|
|
|
|
|||||||
По методу наименьших квадратов находят оценки b01,b11 : |
||||||||||
|
|
|
1 |
N |
|
|
1 |
N |
(2.64) |
|
my0 |
= |
∑yi0 , |
mx1 |
= |
∑x1i ; |
|||||
|
|
|||||||||
|
|
|
N i=1 |
|
|
N i=1 |
|
|||
|
|
|
|
N |
N |
N |
(2.65) |
|||
b1 = |
|
N ∑x1i yi0 −∑x1i ∑yi0 |
; |
|||||||
|
|
|
i=1 |
i=1 |
i=1 |
|||||
1 |
|
|
|
N |
|
N |
2 |
|
||
|
|
|
|
|
||||||
|
|
|
N ∑x12i − |
∑x1i |
|
|||||
|
|
|
|
i=1 |
i=1 |
|
|
|||
|
|
|
|
|
1 |
|
|
(2.66) |
||
|
|
|
b0 = my0 −b1 mx1 . |
|
|
|||||
Используя найденные коэффициенты (2.65), (2.66), находят расчетные значения вспомогательной функции f1 (x1 )= b01 +b11x1 и получают ее гра-
фик, который обычно совмещают с экспериментальными точками y0 (x1 )
(рис.2.19).
